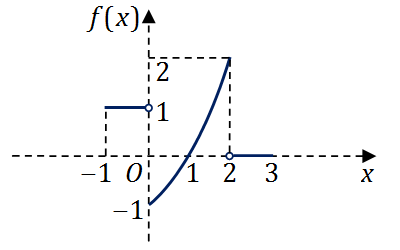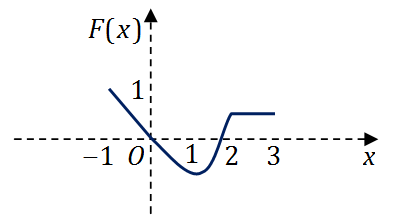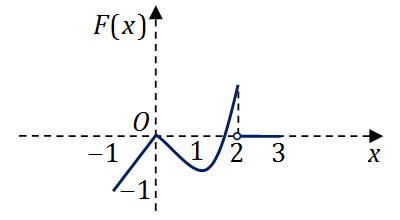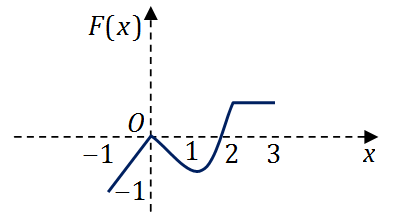2009 年真题
选择题
1
当
x→0
时,
f(x)=x−sinax
与
g(x)=x2ln(1−bx)
等价无穷小,则
正确答案:Af(x)=x−sinax
,
g(x)=x2ln(1−bx)
为等价无穷小,则
x→0limg(x)f(x)=x→0limx2ln(1−bx)x−sinax=x→0limx2⋅(−bx)x−sinax=洛必达x→0lim−3bx21−acosax=洛必达x→0lim−6bxa2sinax=x→0lim−a6b⋅axa2sinax=−6ba3=1⇒a3=−6b
另外,
limx→0−3bx21−acosax
存在,蕴含
1−acosax→0 (x→0)
,故
a=1
,排除 (D)。
所以本题选 (A)。
2
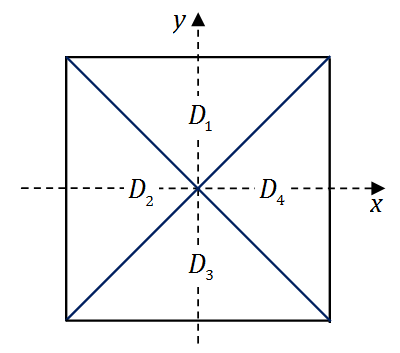
如图,正方形
{(x,y)∣∣x∣≤1,∣y∣≤1}
被其对角线划分为四个区域
Dk(k=1,2,3,4)
,
Ik=∬Dkycosxdxdy
,则
max1≤k≤4{∣Ik∣}=()
正确答案:A本题利用二重积分区域的对称性及被积函数的奇偶性。
D2
、
D4
两区域关于
x
轴对称,而
f(x,−y)=−ycosx=−f(x,y)
,即被积函数是关于
y
的奇函数,所以
I2=I4=0
。
D1
、
D3
两区域关于
y
轴对称,而
f(−x,y)=ycos(−x)=ycosx=f(x,y)
,即被积函数是关于
x
的偶函数,因此:
I1=2∬{(x,y)∣y≥x,0≤x≤1}ycosxdxdy>0
I3=2∬{(x,y)∣y≤−x,0≤x≤1}ycosxdxdy
在
I3
的积分区域内,
y≤−x≤0
且
cosx>0
,故
I3≤0
。
因此,最大值为
I1
。
3
设函数
y=f(x)
在区间
[−1,3]
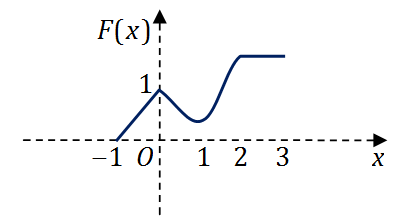
上的图形如下图所示,则函数
F(x)=∫0xf(t)dt
的图形为
正确答案:D此题为定积分的应用知识考核。由
y=f(x)
的图形可见,其图像与
x
轴、
y
轴及
x=x0
所围图形的代数面积为所求函数
F(x)
,从而可得出以下几个方面的特征:
- 当
x∈[0,1]
时,
F(x)≤0
,且单调递减;
- 当
x∈[1,2]
时,
F(x)
单调递增;
- 当
x∈[2,3]
时,
F(x)
为常函数;
- 当
x∈[−1,0]
时,
F(x)≤0
,为线性函数,且单调递增;
- 由于
F(x)
为连续函数,结合上述特点,可见正确选项为 (D)。
4
设有两个数列
{an}
,
{bn}
,若
n→∞liman=0
,则
正确答案:C方法一:举反例:
(A) 取
an=bn=(−1)nn1
,此时
∑bn
收敛但
∑anbn=∑n1
发散,故 (A) 错误;
(B) 取
an=bn=n1
,此时
∑bn
发散但
∑anbn=∑n21
收敛,故 (B) 错误;
(D) 取
an=bn=n1
,此时
∑∣bn∣
发散但
∑an2bn2=∑n41
收敛,故 (D) 错误;
方法二:
因为
limn→∞an=0
,则由定义可知
∃N1
,使得
n>N1
时,有
∣an∣<1
。
又因为
∑n=1∞∣bn∣
收敛,可得
limn→∞∣bn∣=0
,则由定义可知
∃N2
,使得
n>N2
时,有
∣bn∣<1
。
从而,当
n>N1+N2
时,有
an2bn2<∣bn∣
,则由正项级数的比较判别法可知
∑n=1∞an2bn2
收敛。
故答案为 (C)。
5
设
α1
、
α2
、
α3
是 3 维向量空间
R3
的一组基,则由基
α1
、
21α2
、
31α3
到基
α1+α2
、
α2+α3
、
α3+α1
的过渡矩阵为
正确答案:A因为
(η1,η2,⋯,ηn)=(α1,α2,⋯,αn)A
,则
A
称为基
α1,α2,⋯,αn
到
η1,η2,⋯,ηn
的过渡矩阵。
则由基
α1
、
21α2
、
31α3
到
α1+α2
、
α2+α3
、
α3+α1
的过渡矩阵
M
满足:
(α1+α2,α2+α3,α3+α1)=(α1,21α2,31α3)M=(α1,21α2,31α3)120023103 所以此题选(A)。
6
设
A
,
B
均为 2 阶矩阵,
A∗
,
B∗
分别为
A
,
B
的伴随矩阵。若
∣A∣=2
,
∣B∣=3
,则分块矩阵
(OBAO)
的伴随矩阵为
正确答案:B根据
CC∗=∣C∣E
,若
C
可逆,则
C∗=∣C∣C−1
。
分块矩阵
(OBAO)
的行列式为
(OBAO)=(−1)2×2∣A∣∣B∣=2×3=6, 即矩阵可逆。
于是有
(OBAO)∗=OBAO(OBAO)−1=6(OA−1B−1O)=6(O∣A∣1A∗∣B∣1B∗O)=6(O21A∗31B∗O)=(O3A∗2B∗O). 故答案为 (B)。
7
设随机变量
X
的分布函数为
F(x)=0.3Φ(x)+0.7Φ(2x−1)
,其中
Φ(x)
为标准正态分布函数,则
EX=
正确答案:C因为
F(x)=0.3Φ(x)+0.7Φ(2x−1)
,所以
F′(x)=0.3Φ′(x)+20.7Φ′(2x−1).
于是,
EX=∫−∞+∞xF′(x)dx=∫−∞+∞x[0.3Φ′(x)+0.35Φ′(2x−1)]dx=0.3∫−∞+∞xΦ′(x)dx+0.35∫−∞+∞xΦ′(2x−1)dx.
而
∫−∞+∞xΦ′(x)dx=0
。
令
2x−1=u
,则
∫−∞+∞xΦ′(2x−1)dx=2∫−∞+∞(2u+1)Φ′(u)du=2(2×0+1)=2.
所以,
EX=0+0.35×2=0.7.
8
设随机变量
X
与
Y
相互独立,且
X
服从标准正态分布
N(0,1)
,
Y
的概率分布为
P{Y=0}=P{Y=1}=21
,记
FZ(z)
为随机变量
Z=XY
的分布函数,则函数
FZ(z)
的间断点个数为
正确答案:BFZ(z)=P(XY≤z)=P(XY≤z∣Y=0)P(Y=0)+P(XY≤z∣Y=1)P(Y=1)=21[P(X⋅0≤z∣Y=0)+P(X≤z∣Y=1)]=21[P(0≤z)+P(X≤z)]
由于
X
与
Y
相互独立,因此:
(1) 若
z<0
,则
FZ(z)=21Φ(z)
;
(2) 若
z≥0
,则
FZ(z)=21(1+Φ(z))
。
在
z=0
处,左极限为
21Φ(0)
,右极限为
21(1+Φ(0))
。
由于
Φ(0)=21
,左右极限不相等,故
z=0
为间断点,因此选择 (B)。
填空题
9
(填空题)设函数
f(u,v)
具有连续偏导数,
z=f(x,xy)
,则
∂x∂y∂2z=
【答案】
xf12′′+f2′+xyf22′′
【解析】
∂x∂z=f1′+f2′⋅y
∂x∂y∂2z=xf12′′+f2′+yx⋅f22′′=xf12′′+f2′+xyf22′′
10
(填空题)若二阶常系数线性齐次微分方程
y′′+ay′+by=0
的通解为
y=(C1+C2x)ex
,则非齐次方程
y′′+ay′+by=x
满足条件
y(0)=2
,
y′(0)=0
的解为
y=
【答案】
y=−xex+x+2
【解析】
已知
y=(c1+c2x)ex
,可得
λ1=λ2=1
,因此
a=−2
,
b=1
。
对应的微分方程为
y′′−2y′+y=x
。
设特解
y∗=Ax+B
,代入方程得
y′=A
,
y′′=0
。
代入原方程:
−2A+(Ax+B)=x
比较系数得
A=1
,
−2+B=0
,解得
B=2
。
因此特解为
y∗=x+2
,通解为
y=(c1+c2x)ex+x+2
代入初始条件
y(0)=2
,
y′(0)=0
:
y(0)=c1+2=2⇒c1=0
y′=c2ex+(c1+c2x)ex+1
代入
x=0
,
y′(0)=c2+c1+1=0
,结合
c1=0
得
c2=−1
。
因此所求特解为
y=−xex+x+2
11
(填空题)已知曲线
L:y=x2 (0≤x≤2)
,则
∫Lxds=
______
【答案】
613
【解析】 由题意可知,
x=x
,
y=x2
,且
0≤x≤2
。
则弧长微元为:
ds=(x′)2+(y′)2dx=1+4x2dx 因此所求积分为:
利用凑微分法:
∫02x1+4x2dx=81∫021+4x2d(1+4x2) 计算得:
81⋅32(1+4x2)302=121[(1+8)3/2−1]=121(27−1)=1226=613 故:
∫Lxds=613
12
(填空题)设
Ω={(x,y,z)∣x2+y2+z2≤1}
,则
∭Ωz2dxdydz=
【答案】
154π
【解析】
方法一:
∭z2dxdydz=∫02πdθ∫0πdφ∫01ρ2sinφ⋅ρ2cos2φdρ
=2π⋅[−3cos3φ]0π⋅51=154π
方法二:
由轮换对称性可知
∭Ωz2dxdydz=∭Ωx2dxdydz=∭Ωy2dxdydz
因此
32π∫0πsinφdφ∫01r4dr=154π
13
(填空题)若
3
维列向量
α
、
β
满足
αTβ=2
,其中
αT
为
α
的转置,则矩阵
βαT
的非零特征值为。
【答案】 2
【解析】
因为
αTβ=2
,所以
βαTβ=β(αTβ)=2⋅β
故
βαT
的非零特征值为
2
。
14
(填空题)设
X1
,
X2
,
⋯
,
Xm
为来自二项分布总体
B(n,p)
的简单随机样本,
Xˉ
和
S2
分别为样本均值和样本方差,若
Xˉ+kS2
为
np2
的无偏估计量,则
k=
【答案】 -1
【解析】
因为
Xˉ+kS2
是
np2
的无偏估计,所以有
E(Xˉ+kS2)=np2.
代入期望得
np+knp(1−p)=np2.
两边同时除以
n
并化简得
p+kp(1−p)=p2,
即
1+k(1−p)=p.
整理得
k(1−p)=p−1,
因此
k=−1.
解答题
15
(本题满分 9 分)
求二元函数
f(x,y)=x2(2+y2)+ylny
的极值。
【答案】 极小值为
−e1
,在点
(0,e1)
处取得。
【解析】
求二元函数
f(x,y)=x2(2+y2)+ylny
的极值。
解析
fx′(x,y)=2x(2+y2)=0
,
fy′(x,y)=2x2y+lny+1=0
,
故
x=0
,
y=e1
。
二阶偏导数为:
fxx′′=2(2+y2),fyy′′=2x2+y1,fxy′′=4xy.
在点
(0,e1)
处有:
fxx′′∣(0,e1)=2(2+e21),fxy′′(0,e1)=0,fyy′′(0,e1)=e. 由于
fxx′′>0
,且
(fxy′′)2−fxx′′fyy′′<0
,
因此二元函数在极小值
f(0,e1)=−e1
处取得极小值。
16
(本题满分
9
分)
设
an
为曲线
y=xn
与
y=xn+1
(
n=1,2,…
)所围成区域的面积,记
S1=∑n=1∞an
,
S2=∑n=1∞a2n−1
,求
S1
与
S2
的值。
【答案】
S1=21
,
S2=1−ln2
【解析】 由题意,
y=xn
与
y=xn+1
(
n=1,2,…
)在点
x=0
和
x=1
处相交。
所以
an=∫01(xn−xn+1)dx=(n+11xn+1−n+21xn+2)01=n+11−n+21. 从而
S1=n=1∑∞an=N→∞limn=1∑Nan=N→∞lim(21−31+⋯+N+11−N+21)=N→∞lim(21−N+21)=21.
又
S2=n=1∑∞a2n−1=n=1∑∞(2n1−2n+11)=(21−31+⋯+2N1−2N+11)=21−31+41−51+61−⋯
由
ln(1+x)=x−21x2+⋯+(−1)n−1nxn+⋯
,取
x=1
得
ln2=1−(21−31+41−⋯)=1−S2⇒S2=1−ln2.
17
(本题满分 11 分)
曲面
S1
是椭圆
4x2+3y2=1
绕
x
轴旋转而成,圆锥面
S2
是过点
(4,0)
且与椭圆
4x2+3y2=1
相切的直线绕
x
轴旋转而成。
(I) 求
S1
及
S2
的方程;
(II) 求
S1
与
S2
之间的立体体积。
【答案】
(I)
S1
的方程为
4x2+3y2+z2=1
,
S2
的方程为
y2+z2=(21x−2)2
。
(II)
π
解析】**
(I)
S1
的方程为
4x2+3y2+z2=1
。过点
(4,0)
与椭圆
4x2+3y2=1
的切线为
y=±(21x−2)
,因此
S2
的方程为
y2+z2=(21x−2)2
。
(II)
S1
与
S2
之间的体积等于一个底面半径为
23
、高为
3
的圆锥体积
49π
与部分椭球体积
V
之差。其中
V=43π∫12(4−x2)dx=45π
,故所求体积为
49π−45π=π
。
18
(本题满分 11 分)
(I) 证明拉格朗日中值定理:若函数
f(x)
在
[a,b]
上连续,在
(a,b)
内可导,则存在
ξ∈(a,b)
,使得
f(b)−f(a)=f′(ξ)(b−a)
。
(II) 证明:若函数
f(x)
在
x=0
处连续,在
(0,δ)(δ>0)
内可导,且
limx→0+f′(x)=A
,则
f+′(0)
存在,且
f+′(0)=A
。
【答案】 见解析
【解析】 (I) 作辅助函数
φ(x)=f(x)−f(a)−b−af(b)−f(a)(x−a)
,易验证
φ(x)
满足
φ(a)=φ(b)
;
φ(x)
在闭区间
[a,b]
上连续,在开区间
(a,b)
内可导,且
φ′(x)=f′(x)−b−af(b)−f(a)
。
根据罗尔定理,可得在
(a,b)
内至少有一点
ξ
,使
φ′(ξ)=0
,即
f′(ξ)−b−af(b)−f(a)=0,∴f(b)−f(a)=f′(ξ)(b−a).
(II) 任取
x0∈(0,δ)
,则函数
f(x)
满足:在闭区间
[0,x0]
上连续,开区间
(0,x0)
内可导。
从而由拉格朗日中值定理可得:存在
ξx0∈(0,x0)⊂(0,δ)
,使得
f′(ξx0)=x0−0f(x0)−f(0).⋯⋯(∗)
又由于
limx→0+f′(x)=A
,对上式(
∗
式)两边取
x0→0+
时的极限可得:
f+′(0)=x0→0+limx0−0f(x0)−f(0)=x0→0+limf′(ξx0)=ξx0→0+limf′(ξx0)=A.
故
f+′(0)
存在,且
f+′(0)=A
。
19
(本题满分
10
分)
计算曲面积分
I=∬∑(x2+y2+z2)23xdydz+ydzdx+zdxdy ,
其中
∑
是曲面
2x2+2y2+z2=4
的外侧。
【答案】
4π
【解析】 考虑曲面积分
I=∬Σ(x2+y2+z2)3/2xdydz+ydxdz+zdxdy, 其中曲面
Σ
由方程
2x2+2y2+z2=4
给出。
计算偏导数如下:
∂x∂((x2+y2+z2)3/2x)=(x2+y2+z2)5/2y2+z2−2x2,
∂y∂((x2+y2+z2)3/2y)=(x2+y2+z2)5/2x2+z2−2y2,
∂z∂((x2+y2+z2)3/2z)=(x2+y2+z2)5/2x2+y2−2z2.
将以上三式相加,得
∂x∂((x2+y2+z2)3/2x)+∂y∂((x2+y2+z2)3/2y)+∂z∂((x2+y2+z2)3/2z)=0.
由于被积函数及其偏导数在点
(0,0,0)
处不连续,作封闭曲面(外侧)
∑1:x2+y2+z2=R2
(
0<R<1
),将原点包含在内,则
∬∑=∬∑1(x2+y2+z2)3/2xdydz+ydxdz+zdxdy. 在
∑1
上,有
x2+y2+z2=R2
,所以
∬∑=∬∑1R3xdydz+ydxdz+zdxdy. 由高斯公式(散度定理),
∬∑1R3xdydz+ydxdz+zdxdy=R31∭Ω3dV,
其中
Ω
是由
∑1
所围成的球体。于是
R31∭Ω3dV=R33⋅34πR3=4π.
20
(本题满分 11 分)
设
A=1−10−11−4−11−2
,
ξ1=−11−2
。
(I) 求满足
Aξ2=ξ1
的所有向量
ξ2
,
A2ξ3=ξ1
的所有向量
ξ3
;
(II) 对 (I) 中的任意向量
ξ2
,
ξ3
,证明
ξ1
,
ξ2
,
ξ3
线性无关。
【答案】
(I) 满足
Aξ2=ξ1
的所有向量
ξ2
为
ξ2=k11−12+001
,其中
k1
为任意常数。
满足
A2ξ3=ξ1
的所有向量
ξ3
为
ξ3=k2−110+k3001+−2100
,其中
k2,k3
为任意常数。
(II) 见解析。
【解析】
(I) 解方程
Aξ2=ξ1
,其中
(A,ξ1)=1−10−11−4−11−2−11−2→100−102−101−101→100−120−110−110. 由于
r(A)=2
,故有一个自由变量。令
x3=2
,由
Ax=0
解得
x2=−1
,
x1=1
。
求特解时,令
x1=x2=0
,得
x3=1
,故
其中
k1
为任意常数。
解方程
A2ξ3=ξ1
,其中
(A2,ξ1)=2−242−24000−11−2→100100000−2100. 故有两个自由变量。令
x2=0
,
x3=t
(
t
为任意常数),由
A2x=0
得
x1=−x2=0
。
取特解为
−2100
,故
ξ3=k2−110+k3001+−2100, 其中
k2,k3
为任意常数。
(II) 证明:设
k1ξ1+k2ξ2+k3ξ3=0
,即
k1−11−2+k2k1′1−12+001+k3k2′−110+k3′001+−2100=000. 整理后可得关于
k1,k2,k3
的线性方程组,其系数行列式为
−11−2001−2100=−1⋅(0⋅0−1⋅(−21))−0+(−21)⋅(1⋅1−0⋅(−2))=−21+(−21)=−1=0. 故
ξ1,ξ2,ξ3
线性无关。
21
(本题满分 11 分)设二次型
f(x1,x2,x3)=ax12+ax22+(a−1)x32+2x1x3−2x2x3
(I)求二次型
f
的矩阵的所有特征值;
(II)若二次型
f
的规范形为
y12+y22
,求
a
的值。
【答案】
(I)二次型
f
的矩阵的所有特征值为
a
,
a−2
,
a+1
。
(II)
a=2
。
【解析】
(I)设矩阵
A=a010a−11−1a−1
。
计算特征多项式:
∣λE−A∣=λ−a0−10λ−a1−11λ−a+1=(λ−a)λ−a11λ−a+1−0−1λ−a1=(λ−a)[(λ−a)(λ−a+1)−1]−[0+(λ−a)]=(λ−a)[(λ−a)(λ−a+1)−2]=(λ−a)[λ2−2aλ+λ+a2−a−2]=(λ−a){[aλ+21(1−2a)]2−49}=(λ−a)(λ−a+2)(λ−a−1) 因此,特征值为
λ1=a,λ2=a−2,λ3=a+1
(II)若规范形为
y12+y22
,说明有两个正特征值,一个零特征值。
分情况讨论:
- 若
λ1=a=0
,则
λ2=−2<0
,
λ3=1>0
,不符合题意。
- 若
λ2=0
,即
a=2
,则
λ1=2>0
,
λ3=3>0
,符合题意。
- 若
λ3=0
,即
a=−1
,则
λ1=−1<0
,
λ2=−3<0
,不符合题意。
综上所述,
a=2
。
22
(本题满分 11 分)袋中有
1
个红色球、
2
个黑色球与
3
个白球,现有放回地从袋中取两次,每次取一球,以
X
、
Y
、
Z
分别表示两次取球所取得的红球、黑球与白球的个数。
(I) 求
P{X=1∣Z=0}
;
(II) 求二维随机变量
(X,Y)
的概率分布。
【答案】
(I)
P{X=1∣Z=0}=94
(II) 二维随机变量
(X,Y)
的概率分布为:
X∖Y0120416136113191029100
【解析】
(I) 在没有取白球的情况下取了一次红球,利用压缩样本空间则相当于只有
1
个红球、
2
个黑球放回摸两次,其中摸了一个红球。
因此,
P(X=1∣Z=0)=C31⋅C31C21×2=94.
(II)
X
、
Y
的取值范围为
0,1,2
,故
P(X=0,Y=0)=C61⋅C61C31⋅C31=41,P(X=1,Y=0)=C61⋅C61C21⋅C31=61,P(X=2,Y=0)=C61⋅C611=361,P(X=0,Y=1)=C61⋅C61C21⋅C21⋅C31=31,P(X=1,Y=1)=C61⋅C61C21⋅C21=91,P(X=2,Y=1)=0,P(X=0,Y=2)=C61⋅C61C21⋅C21=91,P(X=1,Y=2)=0,P(X=2,Y=2)=0.
联合分布表如下:
X∖Y0120416136113191029100
23
(本题满分 11 分)设总体
X
的概率密度为
f(x)={λ2xe−λx,0,x>0其他
其中参数
λ(λ>0)
未知,
X1,X2,⋯,Xn
是来自总体
X
的简单随机样本。
(I) 求参数
λ
的矩估计量;
(II) 求参数
λ
的最大似然估计量。
【答案】
(I) 参数
λ
的矩估计量为
λ^=Xˉ2
。
(II) 参数
λ
的最大似然估计量为
λ^=Xˉ2
。
【解析】
(1) 由
EX=Xˉ
,而
EX=∫0+∞λ2x2e−λxdx=λ2=Xˉ⇒λ^=Xˉ2
为总体的矩估计量。
(2) 构造似然函数
L(x1,⋯,xn;λ)=i=1∏nf(xi;λ)=λ2n⋅i=1∏nxi⋅e−λ∑i=1nxi.
取对数
lnL=2nlnλ+i=1∑nlnxi−λi=1∑nxi.
令
dλdlnL=0⇒λ2n−i=1∑nxi=0⇒λ=∑i=1nxi2n=n1∑i=1nxi2.
故其最大似然估计量为
λ^=Xˉ2
。