2024 年真题

选择题

1

已知函数 $f(x)=\int_{0}^{x}e^{\cos t}dt$ ， $g(x)=\int_{0}^{\sin x}e^{t^{2}}dt$ ，则( )

正确答案：C

解析：由于 $e^{\cos t}$ 是偶函数，所以 $f(x)=\int_{0}^{x}e^{\cos t}dt$ 是奇函数，又 $g^{\prime}(x)=e^{(\sin x)^{2}}\cos x$ 是偶函数，所以 $g(x)$ 是奇函数。

故选 C。

2

已知 $P = P(x,y,z)$ ， $Q = Q(x,y,z)$ 均连续， $\sum$ 为 $z = \sqrt{1 - x^{2}-y^{2}}$ ， $x\leq0$ ， $y\geq0$ 的上侧，则 $\iint_{\sum}P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}x\mathrm{d}z=$

高等数学多元函数积分学第二类曲面积分

正确答案：A

由转换投影公式。

\begin{aligned} &\iint_{\Sigma}P\cdot\left(-\frac{\partial z}{\partial x}\right)\mathrm{d}x\mathrm{d}y + Q\cdot\left(-\frac{\partial z}{\partial y}\right)\mathrm{d}x\mathrm{d}y\\ =&\iint_{\Sigma}\left[P\cdot\left(\frac{x}{z}\right)+Q\cdot\left(\frac{y}{z}\right)\right]\mathrm{d}x\mathrm{d}y\\ =&\iint_{\Sigma}\left(\frac{Px}{z}+\frac{Qy}{z}\right)\mathrm{d}x\mathrm{d}y \end{aligned}

选 A。

3

已知幂级数 $\sum_{n = 0}^{\infty}a_{n}x^{n}$ 的和函数为 $\ln(2 + x)$ ，则 $\sum_{n = 0}^{\infty}na_{2n}=$ （）

高等数学无穷级数幂级数的和函数及幂级数展开式

正确答案：A

【解析】

\begin{align*} \ln(2 + x) &= \ln\!\left(1+\frac{x}{2}\right)+\ln 2 \\ &= \ln 2 + \sum_{n = 1}^{\infty}(-1)^{n - 1}\frac{\left(\frac{x}{2}\right)^{n}}{n} \\ &= \ln 2 + \frac{x}{2} - \frac{\left(\frac{x}{2}\right)^{2}}{2} + \frac{\left(\frac{x}{2}\right)^{3}}{3} - \frac{\left(\frac{x}{2}\right)^{4}}{4} + \cdots - \frac{\left(\frac{x}{2}\right)^{6}}{6} + \cdots \end{align*}

\begin{align*} \sum_{n = 0}^{\infty} n a_{2n} &= 0 + a_{2} + 2a_{4} + 3a_{6} + 4a_{8} + \cdots \\[4pt] &= -\frac{1}{2 \cdot 2^{2}} + 2 \cdot \left(-\frac{1}{2^{4} \cdot 4}\right) - 3 \cdot \frac{1}{2^{6} \cdot 6} + \cdots \\[4pt] &= -\left[ \frac{1}{2^{3}} + \frac{1}{2^{5}} + \frac{1}{2^{7}} + \cdots \right] \\[4pt] &= -\left[ \frac{\frac{1}{2^{3}}}{1 - \frac{1}{2^{2}}} \right] = -\frac{\frac{1}{8}}{\frac{3}{4}} = -\frac{1}{8} \times \frac{4}{3} = -\frac{1}{6} \end{align*}

故选 A。

4

设函数 $f(x)$ 在区间 $(-1,1)$ 上有定义，且 $\lim\limits_{x \to 0}f(x)=0$ ，则( )

高等数学一元函数微分学导数与微分的概念

正确答案：B

因为 $f^{\prime}(0)=m$ ，所以 $f(x)$ 在 $x = 0$ 处连续，

从而 $\lim\limits_{x \to 0}f(x)=f(0)=0$ ，所以 $\lim\limits_{x \to 0}\frac{f(x)}{x}=\lim\limits_{x \to 0}\frac{f(x)-f(0)}{x - 0}=m$ ，

故选 B.

对于 A 选项， $\lim\limits_{x \to 0}\frac{f(x)}{x}=m$ ，推不出来 $f^{\prime}(0)=m$ ；

对于C选项， $f^{\prime}(x)$ 在 $x = 0$ 处不一定连续；

对于D选项， $f^{\prime}(x)$ 在 $x = 0$ 处极限未必存在。

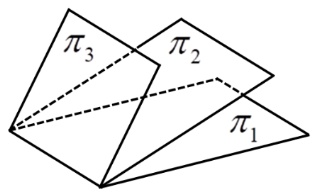
5

在空间直角坐标系 $O - xyz$ 中，三张平面
$\pi_{i} : a_{i}x + b_{i}y + c_{i}z = d_{i} \quad (i = 1,2,3)$ 的位置关系如图所示，
记 $\alpha_{i} = (a_{i}, b_{i}, c_{i})$ ， $\beta_{i} = (a_{i}, b_{i}, c_{i}, d_{i})$ ，
若

r\begin{pmatrix} \alpha_{1} \\ \alpha_{2} \\ \alpha_{3} \end{pmatrix} = m, \quad r\begin{pmatrix} \beta_{1} \\ \beta_{2} \\ \beta_{3} \end{pmatrix} = n,

则（）

线性代数线性方程组

正确答案：B

【解析】
由题意知

\begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix}

有无穷多解，故

r \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{pmatrix} = r \begin{pmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \end{pmatrix} < 3

又由存在两平面的法向量不共线即线性无关，故

r \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{pmatrix} \geq 2

则

r \begin{pmatrix} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{pmatrix} = r \begin{pmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \end{pmatrix} = 2

故 $m = n = 2$ ，故选 B。

6

设向量 $\alpha_{1} = \begin{pmatrix} a \\ 1 \\ -1 \\ 1 \end{pmatrix}$ ， $\alpha_{2} = \begin{pmatrix} 1 \\ 1 \\ b \\ a \end{pmatrix}$ ， $\alpha_{3} = \begin{pmatrix} 1 \\ a \\ -1 \\ 1 \end{pmatrix}$ ，若 $\alpha_{1}, \alpha_{2}, \alpha_{3}$ 线性相关，且其中任意两个向量均线性无关，则（）

线性代数向量向量组的线性相关性

正确答案：D

【解析】
由于向量组 $\alpha_1, \alpha_2, \alpha_3$ 线性相关，因此其秩 $r(\alpha_1, \alpha_2, \alpha_3) < 3$ 。
由此可得行列式

\begin{vmatrix} a & 1 & 1 \\ 1 & 1 & a \\ 1 & a & 1 \end{vmatrix} = 0

解得 $a = 1$ 或 $a = -2$ 。

当 $a = 1$ 时， $\alpha_1$ 与 $\alpha_3$ 线性相关，与题意矛盾，因此舍去。
故取 $a = -2$ 。

进一步，由

\begin{vmatrix} a & 1 & 1 \\ 1 & 1 & a \\ -1 & b & -1 \end{vmatrix} = \begin{vmatrix} -2 & 1 & 1 \\ 1 & 1 & -2 \\ -1 & b & -1 \end{vmatrix} = 0

解得 $b = 2$ 。

因此，正确答案为 D。

7

设 $A$ 是秩为 $2$ 的 $3$ 阶矩阵， $\alpha$ 是满足 $A\alpha = 0$ 的非零向量，若对满足 $\beta^{T}\alpha = 0$ 的 $3$ 维列向量 $\beta$ ，均有 $A\beta=\beta$ ，则( )

线性代数矩阵矩阵的秩

正确答案：A

【解析】由 $A\alpha = 0$ 且 $\alpha\neq 0$ ，故 $\lambda_{1}=0$ ，设非零向量 $\beta_{1},\beta_{2}$ 线性无关（因为与 $\alpha$ 垂直的平面中一定存在两个线性无关的向量）且满足 $\beta_{1}^{T}\alpha=\beta_{2}^{T}\alpha = 0$ ，则 $A\beta_{1}=\beta_{1},A\beta_{2}=\beta_{2}$ ，又由 $\beta_{1},\beta_{2}$ 线性无关，故 $\lambda = 1$

至少为二重根，故 $\lambda_1 = 0, \lambda_2 = \lambda_3 = 1$ ，故 $A^3$ 的特征值为 $0, 1, 1$ ，故 $tr(A^3)=0 + 1 + 1 = 2$ ，故选A.

8

设随机变量 $X$ ， $Y$ 相互独立，且 $X$ 服从正态分布 $N(0,2)$ ， $Y$ 服从正态分布 $N(-2,2)$ ，若 $P\{2X + Y < a\} = P\{X > Y\}$ ，则 $a = ($ )

概率论与数理统计随机变量及其分布

正确答案：B

【解析】 $2X + Y: N(-2,10)$ ， $Y - X: N(-2,2^{2})$ ，

所以 $P\{2X + Y < a\} = \varPhi(\frac{a + 2}{\sqrt{10}})=P\{Y - X < 0\} = \varPhi(\frac{0 + 2}{2})$ ，

于是 $\frac{a + 2}{\sqrt{10}} = \frac{0 + 2}{2}$ ， $a = -2 + \sqrt{10}$ 。

故选 B.

9

设随机变量 $X$ 的概率密度为

f(x) = \begin{cases} 2(1 - x), & 0 < x < 1 \\ 0, & \text{其它} \end{cases}

在 $X = x \ (0 < x < 1)$ 的条件下，随机变量 $Y$ 服从区间 $(x, 1)$ 上的均匀分布，则 $\mathrm{Cov}(X, Y) =$ （）

概率论与数理统计多维随机变量及其分布协方差与相关系数

正确答案：D

【解析】当 $0 < x < 1$ 时，条件概率密度函数为：

f_{Y \mid X}(y \mid x) = \begin{cases} \dfrac{1}{1 - x}, & x < y < 1 \\ 0, & \text{其他} \end{cases}

联合概率密度函数为：

f(x, y) = \begin{cases} 2, & x < y < 1,\ 0 < x < 1 \\ 0, & \text{其他} \end{cases}

计算 $EXY$ ：

EXY = \iint\limits_{\substack{-\infty < x < +\infty \\ -\infty < y < +\infty}} xy f(x, y) \, dx \, dy = \int_{0}^{1} dy \int_{0}^{y} 2xy \, dx = \frac{1}{4}

计算 $EX$ ：

EX = \int_{0}^{1} x \cdot 2(1 - x) \, dx = \frac{1}{3}

计算 $EY$ ：

EY = \iint\limits_{\substack{-\infty < x < +\infty \\ -\infty < y < +\infty}} y f(x, y) \, dx \, dy = \int_{0}^{1} dy \int_{0}^{y} 2y \, dx = \frac{2}{3}

计算协方差：

\mathrm{Cov}(X, Y) = EXY - EX \cdot EY = \frac{1}{4} - \frac{1}{3} \cdot \frac{2}{3} = \frac{1}{36}

故选 D。

10

设随机变量 $X, Y$ 相互独立，且均服从参数为 $\lambda$ 的指数分布，令 $Z = |X - Y|$ ，则下列随机变量与 $Z$ 同分布的是（）

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

正确答案：D

【解析】令 $Z = |X - Y|$ ，则 $F_Z(z) = P\{Z \leq z\} = P\{|X - Y| \leq z\}$ 。

当 $z < 0$ 时， $F_Z(z) = 0$ ；

当 $z \geq 0$ 时，

\begin{align*} F_Z(z) &= \iint_{|x - y| \leq z} f(x, y) \, dx \, dy = \iint_{|x - y| \leq z} \lambda e^{-\lambda x} \lambda e^{-\lambda y} \, dx \, dy \\ &= 2 \int_{0}^{\infty} dy \int_{y}^{y + z} \lambda e^{-\lambda x} \lambda e^{-\lambda y} \, dx = 1 - e^{-\lambda z} \end{align*}

因此，

F_Z(z) = \begin{cases} 0, & z < 0 \\ 1 - e^{-\lambda z}, & z \geq 0 \end{cases}

显然， $Z = |X - Y|$ 与 $X$ 同分布。

故选 D。

填空题

11

（填空题）若 $\lim_{x \to 0}\frac{(1 + ax^{2})^{\sin x}-1}{x^{3}} = 6$ ，则 $a=$ ______

高等数学函数、极限、连续确定极限中的参数

【答案】 6

【解析】

\begin{align*} \lim_{x \to 0}\frac{(1 + ax^{2})^{\sin x}-1}{x^{3}}&=\lim_{x \to 0}\frac{e^{\sin x\ln(1 + ax^{2})}-1}{x^{3}}\\ &=\lim_{x \to 0}\frac{\sin x\cdot\ln(1 + ax^{2})}{x^{3}}\\ &=\lim_{x \to 0}\frac{ax^{3}}{x^{3}} = 6 \end{align*}

故 $a = 6$

12

（填空题）设函数 $f(u,v)$ 具有 2 阶连续偏导数，且

df|_{(1,1)} = 3 \, du + 4 \, dv,

令 $y = f(\cos x, 1 + x^2)$ ，则

\left. \frac{d^2 y}{dx^2} \right|_{x=0} =

高等数学多元函数微分学偏导数的概念与计算

【答案】 5

【解析】
由 $df|_{(1,1)} = 3\,du + 4\,dv$ 可知，

f_u'(1,1) = 3, \quad f_v'(1,1) = 4

又

\frac{dy}{dx} = f_u' \cdot (-\sin x) + f_v' \cdot 2x

则

\begin{align*} \frac{d^2y}{dx^2} &= \left[ f_{uu}'' \cdot (-\sin x) + f_{uv}'' \cdot 2x \right] (-\sin x) + f_u' \cdot (-\cos x) \\ &\quad + \left[ f_{vu}'' \cdot (-\sin x) + f_{vv}'' \cdot 2x \right] (2x) + 2f_v' \end{align*}

因此，

\frac{d^2y}{dx^2} \bigg|_{x=0} = f_u'(1,1) \cdot (-1) + 2f_v'(1,1) = -3 + 8 = 5

13

（填空题）已知函数 $f(x)=x + 1$ ，若 $f(x)=\frac{a_{0}}{2}+\sum_{n = 1}^{\infty}a_{n}\cos nx$ ， $x\in[0,\pi]$ ，则 $\lim_{n\rightarrow\infty}n^{2}\sin a_{2n - 1}=$ __________

高等数学无穷级数幂级数的和函数及幂级数展开式

【答案】 $-\frac{1}{\pi}$

【解析】
由题意可得将 $f(x)$ 在 $[0, \pi]$ 展为余弦级数，由公式可得

\begin{align*} a_{n}&=\frac{2}{\pi}\int_{0}^{\pi}(x + 1)\cos\frac{n\pi x}{\pi}dx\\ &=\frac{2}{\pi}\left[(x + 1)\frac{1}{n}\sin nx+\frac{1}{n^{2}}\cos nx\right]_0^{\pi}\\ &=-\frac{4}{n^{2}\pi},n = 2k - 1 \end{align*}

\lim_{n \to \infty}n^{2}\sin a_{2n - 1}=\lim_{n \to \infty}\left[-\frac{4}{(2n - 1)^{2}\pi}n^{2}\right]=-\frac{1}{\pi}

14

（填空题）微分方程 $y'=\frac{1}{(x + y)^2}$ 满足条件 $y(1)=0$ 的解为______

高等数学常微分方程可分离变量的微分方程与齐次方程

【答案】 $x=\tan(y+\frac{\pi}{4})-y$

【解析

令 $x + y = u$ ，等式两边同时对 $x$ 求导，得到 $u' = 1 + y'$ ，代入原式可得 $u' - 1=\frac{1}{u^2}$ 。
整理得 $\frac{du}{dx}=\frac{1 + u^2}{u^2}$ ，即 $\int\frac{u^2}{u^2 + 1}du=\int dx$ 。
求得 $u-\arctan u = x + c$ ，即 $y-\arctan(x + y)=c$ 。
把初始条件代入可得 $c = -\frac{\pi}{4}$ ，解得 $x=\tan(y+\frac{\pi}{4})-y$ 。

15

（填空题）设实矩阵 $A = \begin{pmatrix} a + 1 & a \\ a & a \end{pmatrix}$ ，若对任意实向量 $\alpha = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ ， $\beta = \begin{pmatrix} y_1 \\ y_2 \end{pmatrix}$ ， $(\alpha^{T} A \beta)^{2} \leq \alpha^{T} A \alpha \cdot \beta^{T} A \beta$ 都成立，则 $a$ 的取值范围是______

线性代数矩阵伴随矩阵与可逆矩阵

【答案】 $[0, +\infty)$

【解析】 由题意知： $\alpha^{T}A(\beta\alpha^{T}-\alpha\beta^{T})A\beta \leq 0$ 恒成立。

设函数 $f(x_{1}, x_{2}, y_{1}, y_{2}) = \alpha^{T}A(\beta\alpha^{T}-\alpha\beta^{T})A\beta$ 。

由

\beta\alpha^{T} - \alpha\beta^{T} = \begin{pmatrix} y_{1} \\ y_{2} \end{pmatrix}(x_{1} \ x_{2}) - \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}(y_{1} \ y_{2}) = (x_{1}y_{2} - x_{2}y_{1}) \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix},

则

\begin{align*} A(\beta\alpha^{T} - \alpha\beta^{T})A &= (x_{1}y_{2} - x_{2}y_{1}) \begin{pmatrix} a+1 & a \\ a & a \end{pmatrix} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} a+1 & a \\ a & a \end{pmatrix} \\ &= (x_{1}y_{2} - x_{2}y_{1}) \begin{pmatrix} 0 & -a \\ a & 0 \end{pmatrix}, \end{align*}

故

f(x_{1}, x_{2}, y_{1}, y_{2}) = (x_{1}y_{2} - x_{2}y_{1}) \alpha^{T} \begin{pmatrix} 0 & -a \\ a & 0 \end{pmatrix} \beta = -a(x_{1}y_{2} - x_{2}y_{1})^{2} \leq 0,

可得 $a \geq 0$ 。

16

（填空题）设随机试验每次成功的概率为 $P$ ，现进行 3 次独立重复试验，在至少成功 1 次的条件下，3 次试验全部成功的概率为 $\frac{4}{13}$ ，则 $P=$ ______

概率论与数理统计随机事件和概率

【答案】 $\frac{2}{3}$

【解析】 设随机变量 $X$ 表示三次试验中成功的次数，则 $X:B(3,p)$ ，所以

P\{X = 3|X\geq1\}=\frac{P\{X = 3,X\geq1\}}{P\{X\geq1\}}=\frac{P\{X = 3\}}{P\{X\geq1\}}=\frac{C_{3}^{3}P^{3}}{1 - C_{3}^{0}(1 - P)^{3}}=\frac{4}{13}

\therefore P = \boxed{\frac{2}{3}}

解答题

17

（本题满分10分）

已知平面区域 $D =\{(x,y)|\sqrt{1 - y^{2}}\leq x\leq1, - 1\leq y\leq1\}$ ，计算 $\iint_{D}\frac{x}{\sqrt{x^{2}+y^{2}}}dxdy$

高等数学多元函数积分学重积分的计算

【答案】 $\sqrt{2}-2+\ln(1 + \sqrt{2})$

【解析】

由于积分区域关于 $x$ 轴对称，被积函数关于 $y$ 为偶函数，故

$\iint_{D}\frac{x}{\sqrt{x^{2}+y^{2}}}dxdy = 2\iint_{D_{1}}\frac{x}{\sqrt{x^{2}+y^{2}}}dxdy=2\int_{0}^{1}dy\int_{\sqrt{1 - y^{2}}}^{1}\frac{x}{\sqrt{x^{2}+y^{2}}}dx$

$=\int_{0}^{1}dy\int_{\sqrt{1 - y^{2}}}^{1}\frac{1}{\sqrt{x^{2}+y^{2}}}d(x^{2}+y^{2})$

$=2\int_{0}^{1}\sqrt{1 + y^{2}}dy - 2=[y\sqrt{1 + y^{2}}+\ln(y+\sqrt{1 + y^{2}})]\big|_{0}^{1}-2$

$=\sqrt{2}-2+\ln(1 + \sqrt{2})$

18

（本题满分12分）

已知函数 $f(x,y)=x^{3}+y^{3}-(x + y)^{2}+3$ ，设 $T$ 是曲面 $z = f(x,y)$ 在点 $(1,1,1)$ 处的切平面， $D$ 为 $T$ 与坐标平面所围成的有界区域在 $xOy$ 平面上的投影。

(1) 求 $T$ 的方程

(2) 求 $f(x,y)$ 在 $D$ 上的最大值和最小值

高等数学多元函数微分学多元函数微分学的几何应用

【答案】
(1) $x + y + z = 3$
(2) 最大值为21，最小值为 $\frac{17}{27}$

【解析】
(1) 对于 $z = f(x,y) = x^{3} + y^{3} - (x + y)^{2} + 3$ ，
有 $z_{x}'(1,1) = -1$ ， $z_{y}'(1,1) = -1$ ，
从而曲面在点 $(1,1,1)$ 处的一个法向量为

n = (-z_{x},-z_{y},1) = (1,1,1),

得该点处曲面的切平面方程为

x + y + z = 3.

(2) 在 $xoy$ 平面中，区域 $D: x + y \leq 3,\; x \geq 0,\; y \geq 0$ 。
在 $D$ 内部求驻点，解方程组

\begin{cases} f_{x}' = 3x^{2} - 2(x + y) = 0,\\ f_{y}' = 3y^{2} - 2(x + y) = 0, \end{cases}

得 $\left(\frac{4}{3},\frac{4}{3}\right)$ ，有 $f\left(\frac{4}{3},\frac{4}{3}\right) = \frac{17}{27}$ ；

在边界 $y = 0,\; 0 < x < 3$ 上，对于 $f(x,0) = x^{3} - x^{2} + 3$ ，
解得其驻点 $\left(\frac{2}{3},0\right)$ ，有 $f\left(\frac{2}{3},0\right) = \frac{77}{27}$ ；

在边界 $x = 0,\; 0 < y < 3$ 上，对于 $f(0,y) = y^{3} - y^{2} + 3$ ，
解得其驻点 $\left(0,\frac{2}{3}\right)$ ，有 $f\left(0,\frac{2}{3}\right) = \frac{77}{27}$ ；

在边界 $x + y = 3,\; 0 < x < 3$ 上，对于 $f(x,3 - x) = x^{3} + (3 - x)^{3} - 6$ ，
解得其驻点 $\left(\frac{3}{2},\frac{3}{2}\right)$ ，有 $f\left(\frac{3}{2},\frac{3}{2}\right) = \frac{3}{4}$ ；

在边界顶点，有

f(0,0) = 3,\quad f(3,0) = f(0,3) = 21.

综上，得 $f(x,y)$ 在 $D$ 上的最大值为 $f(3,0) = f(0,3) = 21$ ，
最小值为 $f\left(\frac{4}{3},\frac{4}{3}\right) = \frac{17}{27}$ 。

19

（本题满分 12 分）

设函数 $f(x)$ 具有 2 阶导数，且 $f^{\prime}(0) = f^{\prime}(1)$ ， $\vert f^{\prime\prime}(x) \vert \leq 1$ ，证明：

(1) 当 $x \in (0, 1)$ 时， $\vert f(x) - f(0)(1 - x) - f(1)x \vert \leq \dfrac{x(1 - x)}{2}$

(2) $\left\vert \int_{0}^{1} f(x) \, dx - \dfrac{f(0) + f(1)}{2} \right\vert \leq \dfrac{1}{12}$

高等数学一元函数微分学微分中值定理

【答案】 见解析

【解析】

(1) 证明：
令 $g(x) = f(0)(1 - x) + f(1)x$ 。
令 $F(x) = f(x) - g(x) - \frac{x(1 - x)}{2}$ ，其中 $x \in (0,1)$ 。
由于 $F(0) = 0$ ， $F(1) = 0$ ，
且 $F^{\prime\prime}(x) = f^{\prime\prime}(x) + 1 \geq 0$ （因为 $\vert f^{\prime\prime}(x) \vert \leq 1$ ），
因此 $F(x)$ 为凹函数，从而 $F(x) \geq 0$ 。
于是有

f(x) - f(0)(1 - x) - f(1)x \leq \frac{x(1 - x)}{2}.

再令 $F(x) = f(x) - g(x) + \frac{x(1 - x)}{2}$ ，其中 $x \in (0,1)$ 。
由于 $F(0) = 0$ ， $F(1) = 0$ ，
且 $F^{\prime\prime}(x) = f^{\prime\prime}(x) - 1 \leq 0$ （因为 $\vert f^{\prime\prime}(x) \vert \leq 1$ ），
因此 $F(x)$ 为凸函数，从而 $F(x) \geq 0$ 。
于是有

f(x) - f(0)(1 - x) - f(1)x \geq -\frac{x(1 - x)}{2}.

综上，

\left\vert f(x) - f(0)(1 - x) - f(1)x \right\vert \leq \frac{x(1 - x)}{2}.

(2) 由 (1) 中

f(x) - f(0)(1 - x) - f(1)x \leq \frac{x(1 - x)}{2},

两边在 $[0,1]$ 上积分得

\int_{0}^{1} \left[ f(x) - f(0)(1 - x) - f(1)x \right] \, dx \leq \int_{0}^{1} \frac{x(1 - x)}{2} \, dx.

计算可得

\int_{0}^{1} f(x) \, dx - \frac{f(0) + f(1)}{2} \leq \frac{1}{12}.

又由 (1) 中

f(x) - f(0)(1 - x) - f(1)x \geq -\frac{x(1 - x)}{2},

两边在 $[0,1]$ 上积分得

\int_{0}^{1} \left[ f(x) - f(0)(1 - x) - f(1)x \right] \, dx \geq -\int_{0}^{1} \frac{x(1 - x)}{2} \, dx,

即

\int_{0}^{1} f(x) \, dx - \frac{f(0) + f(1)}{2} \geq -\frac{1}{12}.

综上，

\left\vert \int_{0}^{1} f(x) \, dx - \frac{f(0) + f(1)}{2} \right\vert \leq \frac{1}{12}.

20

（本题满分12分）

已知有向曲线 L 的球面 $x^{2}+y^{2}+z^{2}=2x$ 与平面 $2x - z - 1 = 0$ 的交线，从 z 轴正向往 z 轴负向看去为逆时针方向，计算曲线积分

$\int_{L}(6xyz - yz^{2})dx + 2x^{2}zdy + xyzdz$

高等数学多元函数积分学第二类曲线积分

【答案】 $\frac{4\sqrt{5}\pi}{25}$

【解析】

\begin{align*} I&=\oint_{L}(6xyz - yz^{2})\,dx + 2x^{2}z\,dy + xyz\,dz \\ &=\iint_{\sum} \begin{vmatrix} dy\,dz & dz\,dx & dx\,dy \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ 6xyz - yz^{2} & 2x^{2}z & xyz \end{vmatrix}, \quad\text{其中 }\sum:z = 2x - 1 \text{，取上侧} \\ &=\iint_{\sum}(xz - 2x^{2})\,dy\,dz+(6xy - 3yz)\,dz\,dx+(z^{2}-2xz)\,dx\,dy \\ &=\iint_{\sum}\big[(xz - 2x^{2})(-2)+(6xy - 3yz)\cdot0+(z^{2}-2xz)\big]\,dx\,dy \\ &=\iint_{\sum}(4x^{2}-4xz + z^{2})\,dx\,dy \\ &=\iint_D\Big[4x^{2}-4x(2x - 1)+(2x - 1)^{2}\Big]\,dx\,dy, \qquad D:\frac{(x-\frac{3}{5})^{2}}{(\frac{2}{5})^{2}}+\frac{y^{2}}{(\frac{2}{\sqrt{5}})^{2}}\le 1\\ &=\iint_D 1\,dx\,dy \\ &=\frac{4\sqrt{5}\pi}{25}. \end{align*}

21

（本题满分 12 分）

已知数列 $\{x_n\}$ ， $\{y_n\}$ ， $\{z_n\}$ 满足 $x_0 = -1$ ， $y_0 = 0$ ， $z_0 = 2$ ，且

\begin{cases} x_n = -2x_{n-1} + 2z_{n-1} \\ y_n = -2y_{n-1} - 2z_{n-1} \\ z_n = -6x_{n-1} - 3y_{n-1} + 3z_{n-1} \end{cases}

记 $\alpha_n = \begin{pmatrix} x_n \\ y_n \\ z_n \end{pmatrix}$ ，写出满足 $\alpha_n = A \alpha_{n-1}$ 的矩阵 $A$ ，并求 $A^n$ 及 $x_n$ ， $y_n$ ， $z_n$ 。

线性代数矩阵矩阵的运算与变换

【答案】
矩阵 $A = \begin{pmatrix} -2 & 0 & 2 \\ 0 & -2 & -2 \\ -6 & -3 & 3 \end{pmatrix}$
$A^n = \begin{pmatrix} -4 + (-1)^{n+1} \cdot 2^n & -2 + (-1)^{n+1} \cdot 2^n & 2 \\ 4 + (-1)^n \cdot 2^{n+1} & 2 + (-1)^n \cdot 2^{n+1} & -2 \\ -6 & -3 & 3 \end{pmatrix}$
$x_n = 8 + (-2)^n$ , $y_n = -8 + (-2)^{n+1}$ , $z_n = 12$

【解析】

由题设得

\begin{pmatrix} x_n \\ y_n \\ z_n \end{pmatrix} = \begin{pmatrix} -2 & 0 & 2 \\ 0 & -2 & -2 \\ -6 & -3 & 3 \end{pmatrix} \begin{pmatrix} x_{n-1} \\ y_{n-1} \\ z_{n-1} \end{pmatrix},

即 $\alpha_n = A \alpha_{n-1}$ ，
故

A = \begin{pmatrix} -2 & 0 & 2 \\ 0 & -2 & -2 \\ -6 & -3 & 3 \end{pmatrix}.

由 $|\lambda E - A| = 0$ ，即

\begin{vmatrix} \lambda + 2 & 0 & -2 \\ 0 & \lambda + 2 & 2 \\ 6 & 3 & \lambda - 3 \end{vmatrix} = 0,

得 $\lambda_1 = 0$ ， $\lambda_2 = 1$ ， $\lambda_3 = -2$ 。

当 $\lambda_1 = 0$ 时， $A x = 0$ ，得基础解系为 $\eta_1 = (1, -1, 1)^T$ 。

当 $\lambda_2 = 1$ 时， $(E - A) x = 0$ ，得基础解系为 $\eta_2 = (2, -2, 3)^T$ 。

当 $\lambda_3 = -2$ 时， $(-2E - A) x = 0$ ，得基础解系为 $\eta_3 = (-1, 2, 0)^T$ 。

故存在可逆矩阵

P = (\eta_1, \eta_2, \eta_3) = \begin{pmatrix} 1 & 2 & -1 \\ -1 & -2 & 2 \\ 1 & 3 & 0 \end{pmatrix},

使 $P^{-1} A P = \begin{pmatrix} 0 & & \\ & 1 & \\ & & -2 \end{pmatrix}$ ，即 $A = P \Lambda P^{-1}$ 。

则

A^n = P \Lambda^n P^{-1} = \begin{pmatrix} 1 & 2 & -1 \\ -1 & -2 & 2 \\ 1 & 3 & 0 \end{pmatrix} \begin{pmatrix} 0 & & \\ & 1 & \\ & & -2 \end{pmatrix}^n \begin{pmatrix} 1 & 2 & -1 \\ -1 & -2 & 2 \\ 1 & 3 & 0 \end{pmatrix}^{-1}

= \begin{pmatrix} -4 + (-1)^{n+1} \cdot 2^n & -2 + (-1)^{n+1} \cdot 2^n & 2 \\ 4 + (-1)^n \cdot 2^{n+1} & 2 + (-1)^n \cdot 2^{n+1} & -2 \\ -6 & -3 & 3 \end{pmatrix}.

由 $\alpha_n = A \alpha_{n-1}$ ，得

\alpha_n = A^n \alpha_0 = \begin{pmatrix} -4 + (-1)^{n+1} \cdot 2^n & -2 + (-1)^{n+1} \cdot 2^n & 2 \\ 4 + (-1)^n \cdot 2^{n+1} & 2 + (-1)^n \cdot 2^{n+1} & -2 \\ -6 & -3 & 3 \end{pmatrix} \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix}

= \begin{pmatrix} 8 + (-2)^n \\ -8 + (-2)^{n+1} \\ 12 \end{pmatrix}.

则

x_n = 8 + (-2)^n, \quad y_n = -8 + (-2)^{n+1}, \quad z_n = 12.

22

（本题满分 12 分）

设总体 $X$ 服从 $[0, \theta]$ 上的均匀分布，其中 $\theta \in (0, +\infty)$ 为未知参数， $X_1, X_2, \cdots, X_n$ 是来自总体 $X$ 的简单随机样本，记 $X_{(n)} = \max\{X_1, X_2, \cdots, X_n\}$ ， $T_c = c X_{(n)}$ 。

（1）求 $c$ ，使得 $T_c$ 是 $\theta$ 的无偏估计；

（2）记 $h(c) = E(T_c - \theta)^2$ ，求 $c$ 使得 $h(c)$ 最小。

概率论与数理统计参数估计与假设检验估计量的无偏性

【答案】
(1) $c = \frac{n+1}{n}$
(2) $c = \frac{n+2}{n+1}$

【解析】
(1) $X$ 的概率密度为

f(x) = \begin{cases} \frac{1}{\theta}, & 0 < x < \theta \\ 0, & \text{} \end{cases}

$X$ 的分布函数为

F(x) = \begin{cases} 0, & x < 0 \\ \frac{1}{\theta}x, & 0 \leq x < \theta \\ 1, & x \geq \theta \end{cases}

$X_{(n)}$ 的分布函数为

F_{X_{(n)}}(x) = P\{\max\{X_1, X_2, \cdots, X_n\} \leq x\} = P\{X_1 \leq x, X_2 \leq x, \cdots, X_n \leq x\}

= P\{X_1 \leq x\} \cdot P\{X_2 \leq x\} \cdots P\{X_n \leq x\} = F^n(x)

$X_{(n)}$ 的概率密度为

f_{X_{(n)}}(x) = n F^{n-1}(x) \cdot f(x) = \begin{cases} \frac{n}{\theta^n} x^{n-1}, & 0 < x < \theta \\ 0, & \text{} \end{cases}

计算期望：

E(T_c) = c E(X_{(n)}) = c \int_0^\theta x \cdot \frac{n}{\theta^n} x^{n-1} \, dx = \frac{cn}{n+1} \theta

令 $E(T_c) = \frac{cn}{n+1} \theta = \theta$ ，解得

c = \frac{n+1}{n}

(2) 计算二阶矩：

E(T_c^2) = c^2 E(X_{(n)}^2) = c^2 \int_0^\theta x^2 \cdot \frac{n}{\theta^n} x^{n-1} \, dx = \frac{c^2 n}{n+2} \theta^2

定义函数：

h(c) = E(T_c - \theta)^2 = E(T_c^2 - 2\theta T_c + \theta^2) = E(T_c^2) - 2\theta E(T_c) + \theta^2

代入得

h(c) = \frac{c^2 n}{n+2} \theta^2 - \frac{2cn}{n+1} \theta^2 + \theta^2

求导：

h'(c) = \frac{2cn}{n+2} \theta^2 - \frac{2n}{n+1} \theta^2

令 $h'(c) = 0$ ，解得

c = \frac{n+2}{n+1}

二阶导数为

h''(c) = \frac{2n}{n+2} \theta^2 > 0

因此当 $c = \frac{n+2}{n+1}$ 时， $h(c)$ 取得最小值。