2025 年真题

选择题

1

已知函数 $f(x)=\int_{0}^{x}e^{t^{2}}\sin tdt$ ， $g(x)=\int_{0}^{x}e^{t^{2}}dt\cdot\sin^{2}x$ ，则

高等数学一元函数微分学函数的单调性、极值与最值

正确答案：B

【解析】

$f^\prime(x)=e^{x^2}\sin x,f^{\prime\prime}(x)=2xe^{x^2}\sin x + e^{x^2}\cos x$

$f^\prime(0)=0,f^{\prime\prime}(0)=1\gt0$ 。

$x = 0$ 是 $f(x)$ 的极值点。

$g^\prime(x)=e^{x^2}\sin^2 x + \sin2x\int_{0}^{x}e^{t^2}dt$ ，

$g^{\prime\prime}(x)=e^{x^2}\sin2x + 2xe^{x^2}\sin^2 x + \sin2xe^{x^2} + 2\cos2x\int_{0}^{x}e^{t^2}dt$

$g^\prime(0)=0,\ g^{\prime\prime}(0)=0,\ g^{\prime\prime\prime}(0)\gt0$ 。

$(0,0)$ 是 $y = g(x)$ 的拐点。

2

已知级数：① $\sum_{n = 1}^{\infty}\sin\frac{n^{3}\pi}{n^{2}+1}$ ；② $\sum_{n = 1}^{\infty}(-1)^{n}\left(\frac{1}{\sqrt[3]{n^{2}}}-\tan\frac{1}{\sqrt[3]{n^{2}}}\right)$ ，则

高等数学无穷级数常数项级数敛散性的判定

正确答案：B

【解析】

$\left|\sin\frac{n^{3}\pi}{n^{2}+1}\right|=\left|\sin\left(\frac{n^{3}\pi}{n^{2}+1}-n\pi\right)\right|=\left|\sin\frac{n}{n^{2}+1}\pi\right|\sim\frac{n}{n^{2}+1}\pi\sim\frac{1}{n}\pi$ .

$\sum_{n = 1}^{\infty}\frac{1}{n}$ 发散 $\therefore$ 不是绝对收敛.

$\sin\frac{n^{3}\pi}{n^{2}+1}=(-1)^{n}\sin\left(\frac{n^{3}\pi}{n^{2}+1}-n\pi\right)=(-1)^{n}\sin\frac{n}{n^{2}+1}\pi$ ，为交错级数.

$\sin\frac{n}{n^{2}+1}\pi$ 递减， $\therefore$ 条件收敛.

$\sum_{n = 1}^{\infty}(-1)^{n}\left(\frac{1}{\sqrt[3]{n^{2}}}-\tan\frac{1}{\sqrt[3]{n^{2}}}\right)$ .

$\left|(-1)^{n}\left(\frac{1}{\sqrt[3]{n^{2}}}-\tan\frac{1}{\sqrt[3]{n^{2}}}\right)\right|=\left|-\frac{1}{3}\frac{1}{n^{\frac{2}{3}\times\frac{3}{2}}}+o\left(\frac{1}{n^{2}}\right)\right|$ （注：原解析此处 $n$ 的次数书写可能有误，推测应为 $\left|-\frac{1}{3}\frac{1}{n^{\frac{4}{3}}}+o\left(\frac{1}{n^{\frac{4}{3}}}\right)\right|$ ，按你提供内容提取），实际准确是利用等价无穷小，当 $x\to0$ 时， $x - \tan x\sim-\frac{1}{3}x^{3}$ ，令 $x = \frac{1}{\sqrt[3]{n^{2}}}=n^{-\frac{2}{3}}$ ，则 $\frac{1}{\sqrt[3]{n^{2}}}-\tan\frac{1}{\sqrt[3]{n^{2}}}\sim-\frac{1}{3}n^{-2}$ ，所以 $\left|(-1)^{n}\left(\frac{1}{\sqrt[3]{n^{2}}}-\tan\frac{1}{\sqrt[3]{n^{2}}}\right)\right|\sim\frac{1}{3n^{2}}$ ）

$\sum_{n = 1}^{\infty}\frac{1}{n^{2}}$ 收敛 $\therefore\sum_{n = 1}^{\infty}(-1)^{n}\left(\frac{1}{\sqrt[3]{n^{2}}}-\tan\frac{1}{\sqrt[3]{n^{2}}}\right)$ 绝对收敛

3

设函数 $f(x)$ 在区间 $[0, +\infty)$ 上可导，则

高等数学一元函数微分学微分中值定理

正确答案：D

【解析】A 错误，反例：

$f(x) = \frac{\sin x^2}{x}, \lim\limits_{x \to +\infty} f(x) = 0$ ，但 $\lim\limits_{x \to +\infty} f'(x) = \lim\limits_{x \to +\infty} \frac{2x^2 \cos x^2 - \sin x^2}{x^2}$ ，极限不存在。

B 错误，反例： $f(x) = \sqrt{x}, f'(x) = \frac{1}{2\sqrt{x}}, \lim\limits_{x \to +\infty} f'(x) = 0$ ，极限存在，但 $\lim\limits_{x \to +\infty} f(x)$ 极限不存在。

C 错误，反例：

$f(x) = \cos x$ ，则 $\lim\limits_{x \to +\infty} \frac{\int_{0}^{x} f(t)dt}{x} = \lim\limits_{x \to +\infty} \frac{\sin x}{x}$ 存在，但 $\lim\limits_{x \to +\infty} f(x) = \lim\limits_{x \to +\infty} \cos x$ 不存在。

D 正确，用 $\lim\limits_{x \to +\infty} \frac{\int_{0}^{x} f(t)dt}{x} = \lim\limits_{x \to +\infty} \frac{f(x)}{1} = A$ ，故选 D 。

4

设函数 $f(x, y)$ 连续，则

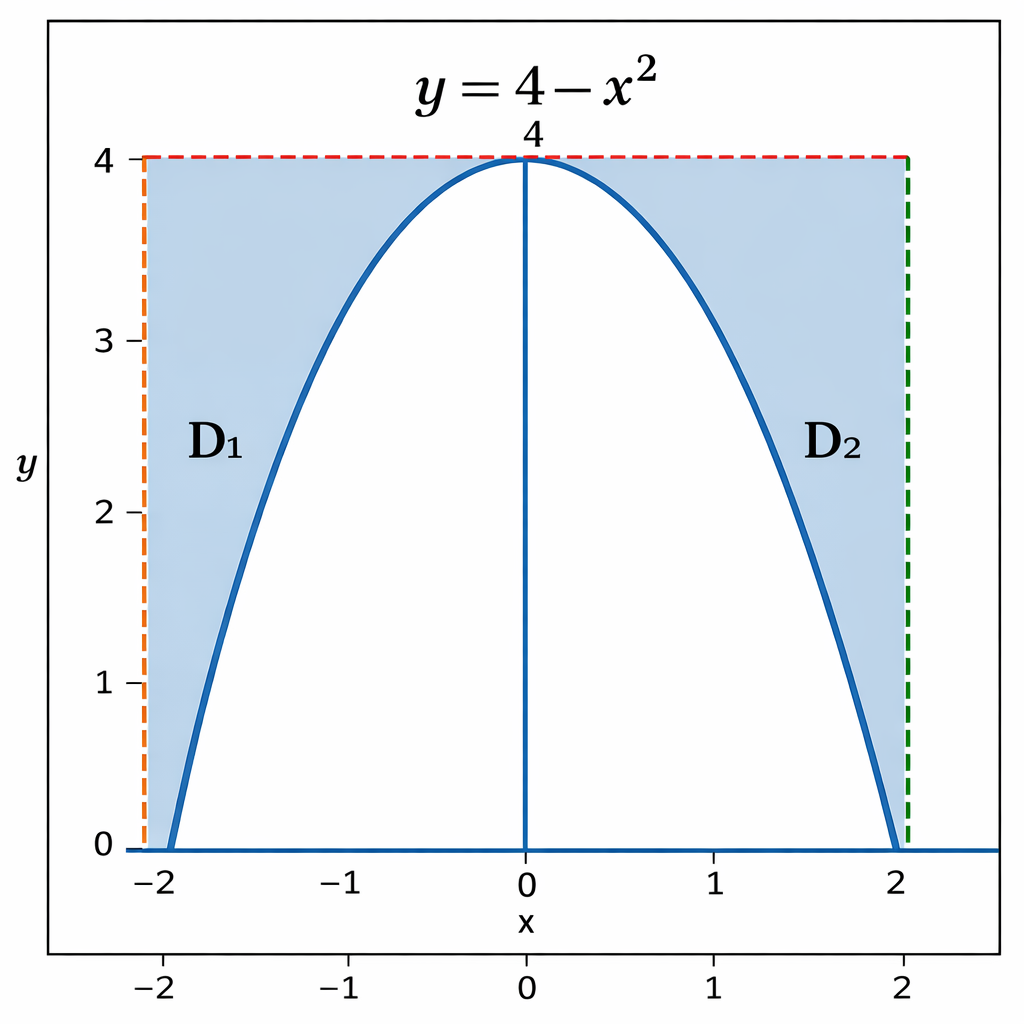
\int_{-2}^{2} dx \int_{4 - x^2}^{4} f(x, y) \, dy =

高等数学多元函数积分学交换积分次序与坐标系之间的转化

正确答案：A

【解析】由题易知，此二重积分的积分区域为
$D = \left\{ (x, y) \middle\vert 4 - x^2 \leq y \leq 4, -2 \leq x \leq 2 \right\}$ ，对应图像为上图所示。

记
$D_1 = \left\{ (x, y) \middle\vert 4 - x^2 \leq y \leq 4, -2 \leq x \leq 0 \right\}$ ，
$D_2 = \left\{ (x, y) \middle\vert 4 - x^2 \leq y \leq 4, 0 \leq x \leq 2 \right\}$ ，
且 $I = \int_{-2}^{2} dx \int_{4 - x^2}^{4} f(x, y) \, dy$ ，
则 $I = \iint_{D_1} f(x, y) \, d\sigma + \iint_{D_2} f(x, y) \, d\sigma$ 。

交换积分次序得

I = \int_{0}^{4} dy \int_{-2}^{-\sqrt{4 - y}} f(x, y) \, dx + \int_{0}^{4} dy \int_{\sqrt{4 - y}}^{2} f(x, y) \, dx

= \int_{0}^{4} \left[ \int_{-2}^{-\sqrt{4 - y}} f(x, y) \, dx + \int_{\sqrt{4 - y}}^{2} f(x, y) \, dx \right] dy

故 A 正确。

5

二次型 $f(x_1, x_2, x_3) = x_1^2 + 2x_1x_2 + 2x_1x_3$ 的正惯性指数

线性代数二次型

正确答案：B

【解析】
矩阵

A = \begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}

计算特征多项式：

\begin{align*} \lambda E - A &= \begin{pmatrix} \lambda - 1 & -1 & -1 \\ -1 & \lambda & 0 \\ -1 & 0 & \lambda \end{pmatrix} \\ &\to \begin{pmatrix} \lambda - 1 & -1 & -1 \\ 0 & \lambda & -\lambda \\ -1 & 0 & \lambda \end{pmatrix} \\ &\to \lambda \begin{pmatrix} \lambda - 1 & -1 & -1 \\ 0 & 1 & -1 \\ -1 & 0 & \lambda \end{pmatrix} \\ &= \lambda \bigl[ \lambda(\lambda - 1) - 1 - 1 \bigr] \\ &= \lambda (\lambda^2 - \lambda - 2) \\ &= \lambda (\lambda - 2)(\lambda + 1) \end{align*}

解得特征值为：

\lambda_1 = 0, \quad \lambda_2 = 2, \quad \lambda_3 = -1

因此，正惯性指数为 $1$ ，选 B。

6

设 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}, \boldsymbol{\alpha}_{4}$ 是 $n$ 维列向量， $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}$ 线性无关， $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}$ 线性相关，且 $\boldsymbol{\alpha}_{1} + \boldsymbol{\alpha}_{2} + \boldsymbol{\alpha}_{4} = \boldsymbol{0}$ 。

在空间直角坐标系 $O - xyz$ 中，关于 $x, y, z$ 的方程组 $x\boldsymbol{\alpha}_{1} + y\boldsymbol{\alpha}_{2} + z\boldsymbol{\alpha}_{3} = \boldsymbol{\alpha}_{4}$ 的几何图形是

线性代数向量向量组的线性相关性

正确答案：D

【解析】记 $A = (\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3})$ ，由 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}$ 线性无关，而 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}$ 线性相关，可得 $r(A) = 2$ 。

记 $\overline{A} = (A \vert \boldsymbol{\alpha}_{4}) = (\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}, \boldsymbol{\alpha}_{4})$ ，再由 $\boldsymbol{\alpha}_{1} + \boldsymbol{\alpha}_{2} + \boldsymbol{\alpha}_{4} = \boldsymbol{0}$ ，可得 $r(\overline{A}) = 2$ 。于是方程 $A \mathbf{x} = \boldsymbol{\alpha}_{4}$ 有无穷多解。

方程 $x \boldsymbol{\alpha}_{1} + y \boldsymbol{\alpha}_{2} + z \boldsymbol{\alpha}_{3} = \boldsymbol{\alpha}_{4}$ 等价于 $(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}) \cdot (x, y, z)^{\mathrm{T}} = \boldsymbol{\alpha}_{4}$ ，即 $A \cdot (x, y, z)^{\mathrm{T}} = \boldsymbol{\alpha}_{4}$ 。

若该方程所表示的平面过原点，则 $\boldsymbol{\alpha}_{4} = \boldsymbol{0}$ ，但这与 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}$ 线性无关矛盾，故平面不过原点。

将方程写为分量形式：

\begin{cases} a_{11}x + a_{12}y + a_{13}z = a_{14} \\ a_{21}x + a_{22}y + a_{23}z = a_{24} \\ \cdots \\ a_{n1}x + a_{n2}y + a_{n3}z = a_{n4} \end{cases}

由上述分析可知 $r(A) = r(\overline{A}) = 2$ ，故该方程组表示两个平面交于一条直线，且不过原点。

因此，正确答案为 D。

7

设 $n$ 阶矩阵 $\boldsymbol{A}$ 、 $\boldsymbol{B}$ 、 $\boldsymbol{C}$ 满足 $r(\boldsymbol{A}) + r(\boldsymbol{B}) + r(\boldsymbol{C}) = r(\boldsymbol{ABC}) + 2n$ ，给出下列四个结论：

① $r(\boldsymbol{ABC}) + n = r(\boldsymbol{AB}) + r(\boldsymbol{C})$ ；
② $r(\boldsymbol{AB}) + n = r(\boldsymbol{A}) + r(\boldsymbol{B})$ ；
③ $r(\boldsymbol{A}) = r(\boldsymbol{B}) = r(\boldsymbol{C}) = n$ ；
④ $r(\boldsymbol{AB}) = r(\boldsymbol{BC}) = n$ 。

其中正确结论的序号是

线性代数矩阵矩阵的秩

正确答案：A

【解析】
设矩阵

\boldsymbol{A} = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}, \quad \boldsymbol{B} = \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}, \quad \boldsymbol{C} = \boldsymbol{E}

满足

r(\boldsymbol{A}) + r(\boldsymbol{B}) + r(\boldsymbol{C}) = r(\boldsymbol{ABC}) + 2n

计算得

r(\boldsymbol{A}) = 1, \quad r(\boldsymbol{B}) = 1, \quad r(\boldsymbol{C}) = 2

因此排除结论③和④，故选 A。

8

设二维随机变量 $(X,Y)$ 服从正态分布 $N(0,0;1,1;\rho)$ ，其中 $\rho\in(-1,1)$ 。若 $a,b$ 为满足 $a^2 + b^2 = 1$ 的任意实数，则 $D(aX + bY)$ 的最大值为

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

正确答案：C

【解析】

$D(aX + bY)=a^2DX + b^2DY + 2ab\rho\cdot1\cdot1$

$= a^2 + b^2 + 2ab\rho = 1 + 2ab\rho = 1 + 2a\sqrt{1 - a^2}\rho = f(a)$

$f^\prime(a)=\rho\left(2\sqrt{1 - a^2} + 2a\cdot\frac{-a}{\sqrt{1 - a^2}}\right)= 2\rho\left(\sqrt{1 - a^2} - \frac{a^2}{\sqrt{1 - a^2}}\right)= 0$

即 $2\rho\cdot\frac{1 - a^2 - a^2}{\sqrt{1 - a^2}} = 0$ ， $2a^2 = 1\Rightarrow a^2 = \frac{1}{2},b^2 = \frac{1}{2}$ ，于是 $a = \pm\frac{1}{\sqrt{2}},b = \pm\frac{1}{\sqrt{2}}$ 。所以最大值为 $1 + |\rho|$ ，故选C。

9

设 $X_{1},X_{2},\cdots,X_{20}$ 是来自总体 $B(1,0.1)$ 的简单随机样本.令 $T = \sum_{i = 1}^{20}X_{i}$ ，利用泊松分布近似表示二项分布的方法可得 $P\{T\leq1\}\approx$

概率论与数理统计大数定律和中心极限定理

正确答案：C

【解析】由题意可知 $T\sim B(20,0.1).np = 20\times0.1 = 2$

$P\{T\leq1\} = P\{T = 0\} + P\{T = 1\} = \frac{2^{0}}{0!}e^{-2} + \frac{2^{1}}{1!}e^{-2} = e^{-2} + 2e^{-2} = \frac{3}{e^{2}}$

10

设 $X_1,X_2,\cdots,X_n$ 为来自正态总体 $N(\mu,2)$ 的简单随机样本，记 $\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$ ， $\bar{x}$ 为 $\bar{X}$ 的观察值， $z_{\alpha}$ 表示标准正态分布的上侧 $\alpha$ 分位数，假设检验问题： $H_0:\mu\leq1,H_1:\mu>1$ 的显著性水平为 $\alpha$ 的检验的拒绝域为（）.

概率论与数理统计参数估计与假设检验假设检验

正确答案：D
【解析】按题意需检验假设:

H_0: \mu \leq 1

，

H_1: \mu > 1

，这是右边检验问题，

\sigma^2 = 2

为已知，其拒绝域为

\frac{\bar{X} - \mu}{\sigma/\sqrt{n}} > z_\alpha

，解得

\bar{X} > \mu + \frac{\sigma}{\sqrt{n}}z_\alpha = 1 + \frac{\sqrt{2}}{\sqrt{n}}z_\alpha

，故选 D.

填空题

11

（填空题）

\lim\limits_{x \to 0^{+}} \frac{x^x - 1}{\ln x \cdot \ln(1 - x)} =

高等数学一元函数微分学微分中值定理

【答案】 $-1$

【解析】

\lim\limits_{x \to 0^{+}} \frac{e^{x\ln x} - 1}{-x\ln x} = \lim\limits_{x \to 0^{+}} \frac{x\ln x}{-x\ln x} = -1

12

（填空题）已知函数 $f(x)=\begin{cases}0, & 0\leq x\lt\frac{1}{2} \\ x^2, & \frac{1}{2}\leq x\leq1 \end{cases}$ 的傅里叶级数为 $\sum_{n = 1}^{\infty}b_n\sin n\pi x$ ， $S(x)$ 为 $\sum_{n = 1}^{\infty}b_n\sin n\pi x$ 的和函数，则 $S\left(-\frac{7}{2}\right)=$ ______．

高等数学无穷级数幂级数的和函数及幂级数展开式

【答案】 $\frac{1}{8}$

【解析】

S\left(-\frac{7}{2}\right)=S\left(-\frac{7}{2}+4\right)=S\left(\frac{1}{2}\right)=\frac{1}{8}

13

（填空题）已知函数 $u(x, y, z) = x y^2 z^3$ ，向量 $\boldsymbol{n} = (2, 2, -1)$ ，则

\left. \frac{\partial u}{\partial \boldsymbol{n}} \right|_{(1,1,1)} =

多元函数微分学方向导数和梯度

【答案】 1

【解析】

由题易知，

\frac{\partial u}{\partial x} = y^{2}z^{3},\quad \frac{\partial u}{\partial y} = 2xyz^{3},\quad \frac{\partial u}{\partial z} = 3xy^{2}z^{2}.

在 $x = 1$ ， $y = 1$ ， $z = 1$ 处，有

\left(\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z}\right) = (1, 2, 3).

对于向量 $\boldsymbol{\bar{n}} = (2, 2, -1)$ ，归一化可得

\boldsymbol{\bar{n}}_{0} = \left(\frac{2}{3}, \frac{2}{3}, -\frac{1}{3}\right).

故

\begin{align*} \left. \frac{\partial u}{\partial \boldsymbol{n}} \right|_{(1,1,1)} &= \left(\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z}\right) \cdot \boldsymbol{\bar{n}}_{0} \\ &= (1, 2, 3) \cdot \left(\frac{2}{3}, \frac{2}{3}, -\frac{1}{3}\right) \\ &= 1 \cdot \frac{2}{3} + 2 \cdot \frac{2}{3} + 3 \cdot \left(-\frac{1}{3}\right) \\ &= 1. \end{align*}

14

（填空题）已知有向曲线 $L$ 是沿抛物线 $y = 1 - x^2$ 从点 $(1,0)$ 到点 $(-1,0)$ 的一段，则曲线积分 $\int_{L} (y + \cos x)dx + (2x + \cos y)dy =$ ______。

高等数学多元函数积分学第二类曲线积分

【答案】 $\frac{4}{3} - 2\sin1$

【解析】

由题易知可作曲线如右图所示。

记 $L_0$ 是从 $x = -1$ 到 $x = 1$ 的直线，

并记曲线积 $I = \int_{L} (y + \cos x)dx + (2x + \cos y)dy$

则在 $L_0$ 与 $L$ 所围的封闭区域可用格林公式

即 $I_1 = \oint_{L_0 + L} (y + \cos x)dx + (2x + \cos y)dy$

$= \iint_{D} 2 - 1d\sigma = \int_{-1}^{1} dx\int_{0}^{1 - x^2} dy = \int_{-1}^{1} (1 - x^2)dx = \frac{4}{3}$

又 $I_2 = \int_{L_0} (y + \cos x)dx + (2x + \cos y)dy = \int_{-1}^{1} \cos xdx = 2\sin1$ ，故 $I = \frac{4}{3} - 2\sin1$

15

（填空题）设矩阵 $\boldsymbol{A} = \begin{pmatrix} 4 & 2 & -3 \\ a & 3 & -4 \\ b & 5 & -7 \end{pmatrix}$ ，若方程组 $\boldsymbol{A}^{2} \boldsymbol{x} = \boldsymbol{0}$ 与 $\boldsymbol{A} \boldsymbol{x} = \boldsymbol{0}$ 不同解，则 $a - b =$ ______。

线性代数矩阵矩阵的运算与变换

【答案】 -4

【解析】 由题知， $\boldsymbol{A} = \begin{pmatrix} 4 & 2 & -3 \\ a & 3 & -4 \\ b & 5 & -7 \end{pmatrix}$ 。若 $\boldsymbol{A}^{2} \boldsymbol{x} = \boldsymbol{0}$ 与 $\boldsymbol{A} \boldsymbol{x} = \boldsymbol{0}$ 同解，则三秩相同，即 $r(\boldsymbol{A}) = r(\boldsymbol{A}^{2}) = r\begin{pmatrix} \boldsymbol{A} \\ \boldsymbol{A}^{2} \end{pmatrix}$ 。

如果 $\boldsymbol{A}$ 可逆，三秩显然相同，则 $\boldsymbol{A}^{2} \boldsymbol{x} = \boldsymbol{0}$ 与 $\boldsymbol{A} \boldsymbol{x} = \boldsymbol{0}$ 同解。于是，要想 $\boldsymbol{A}^{2} \boldsymbol{x} = \boldsymbol{0}$ 与 $\boldsymbol{A} \boldsymbol{x} = \boldsymbol{0}$ 不同解，即 $\boldsymbol{A}$ 不可逆，于是 $\vert \boldsymbol{A} \vert = 0$ 。

根据行列式的倍加性质易得：

\vert \boldsymbol{A} \vert = \begin{vmatrix} 4 & 2 & -3 \\ a & 3 & -4 \\ b & 5 & -7 \end{vmatrix} = \begin{vmatrix} 4 & 2 & -1 \\ a & 3 & -1 \\ b & 5 & -2 \end{vmatrix} = \begin{vmatrix} 4 & 0 & -1 \\ a & 1 & -1 \\ b & 1 & -2 \end{vmatrix} = 4(-2 + 1) - (a - b)

令 $\vert \boldsymbol{A} \vert = 0$ ，有 $a - b = -4$ 。

16

（填空题）设 $A,B$ 为两个不同的随机事件，且 $A$ 与 $B$ 相互独立，已知 $P(A)=2P(B)$ ， $P(A\cup B)=\frac{5}{8}$ ，则在 $A,B$ 至少有一个发生的条件下， $A,B$ 中恰有一个发生的概率为______。

概率论与数理统计随机事件和概率

【答案】 $\frac{4}{5}$

【解析】

\begin{align*} P(A\overline{B}) + P(\overline{A}B) &= P(A) - P(AB) + P(B) - P(AB) \\ &= P(A) + P(B) - 2P(A)P(B) \end{align*}

\begin{align*} P(A\cup B) &= P(A) + P(B) - P(AB) = \frac{5}{8} \\ &\Rightarrow 3P(B) - 2P^{2}(B) = \frac{5}{8} \\ &\Rightarrow 24P(B) - 16P^{2}(B) = 5 \\ &\Rightarrow 16P^{2}(B) - 24P(B) + 5 = 0 \\ &\Rightarrow (4P(B) - 1)(4P(B) - 5) = 0 \\ &\Rightarrow P(B) = \frac{1}{4}, \quad P(A) = \frac{1}{2} \end{align*}

\begin{align*} P(A\overline{B}) + P(\overline{A}B) &= P(A) - P(AB) + P(B) - P(AB) \\ &= P(A) + P(B) - 2P(A)P(B) \\ &= \frac{1}{2} + \frac{1}{4} - 2 \times \frac{1}{4} \times \frac{1}{2} = \frac{1}{2} \end{align*}

P = \frac{\frac{1}{2}}{\frac{5}{8}} = \frac{1}{2} \times \frac{8}{5} = \frac{4}{5}

解答题

17

（本题满分10分）

计算 $\int_{0}^{1}\frac{1}{(x + 1)(x^2 - 2x + 2)}dx$ 。

高等数学一元函数积分学定积分的计算

【答案】 $\frac{3}{10}\ln2 + \frac{1}{10}\pi$

【解析】

\begin{aligned} \int_{0}^{1}\frac{1}{(x + 1)(x^2 - 2x + 2)}dx &= \int_{0}^{1}\left(\frac{A}{x + 1}+\frac{Bx + C}{x^2 - 2x + 2}\right)dx \nonumber \\ &= \int_{0}^{1}\left(\frac{\frac{1}{5}}{x + 1}+\frac{-\frac{1}{5}x+\frac{3}{5}}{x^2 - 2x + 2}\right)dx \nonumber \\ &= \frac{1}{5}\ln|1 + x|\bigg|_{0}^{1} \\ &\quad - \frac{1}{10}\ln|x^2 - 2x + 2|\bigg|_{0}^{1} \\ &\quad + \frac{2}{5}\arctan(x - 1)\bigg|_{0}^{1} \nonumber \\ &= \frac{3}{10}\ln2 + \frac{1}{10}\pi \nonumber \end{aligned}

18

（本题满分12分）

已知函数 $f(u)$ 在区间 $(0, +\infty)$ 内具有2阶导数，记 $g(x, y) = f\left(\frac{x}{y}\right)$ ，若 $g(x, y)$ 满足 $x^2\frac{\partial^2 g}{\partial x^2} + xy\frac{\partial^2 g}{\partial x\partial y} + y^2\frac{\partial^2 g}{\partial y^2} = 1$ ，且 $g(x, x) = 1$ ， $\left.\frac{\partial g}{\partial x}\right\rvert_{(x, x)} = \frac{2}{x}$ ，求 $f(u)$ 。

高等数学多元函数微分学偏导数的概念与计算

【答案】 $f(u) = \frac{1}{2}\ln^2 u + 2\ln u + 1$

【解析】

令 $u = \frac{x}{y}$ ，则

\frac{\partial g}{\partial x} = f'(u)\frac{1}{y},\quad \frac{\partial g}{\partial y} = f'(u)\left(-\frac{x}{y^2}\right).

又

\begin{gather*} g(x, x) = f\left(\frac{x}{x}\right) = f(1) = 1, \\ \left.\frac{\partial g}{\partial x}\right|_{(x, x)} = f'(1)\frac{1}{x} = \frac{2}{x}, \end{gather*}

故 $f'(1) = 2$ 。

二阶偏导数为：

\begin{gather*} \frac{\partial^2 g}{\partial x^2} = \left(f''(u)\frac{1}{y}\right)\frac{1}{y} = f''(u)\frac{1}{y^2} \qquad \text{(1)} \\ \frac{\partial^2 g}{\partial x\partial y} = f''(u)\left(-\frac{x}{y^2}\right)\frac{1}{y} + f'(u)\left(-\frac{1}{y^2}\right) = -\frac{x}{y^3}f''(u) - \frac{1}{y^2}f'(u) \qquad \text{(2)} \\ \frac{\partial^2 g}{\partial y^2} = f''(u)\left(-\frac{x}{y^2}\right)\frac{x}{y} + f'(u)\left(\frac{2x}{y^2}\right) = \frac{x^2}{y^4}f''(u) + \frac{2x}{y^3}f'(u) \qquad \text{(3)} \end{gather*}

将 (1)(2)(3) 代入

x^2\frac{\partial^2 g}{\partial x^2} + xy\frac{\partial^2 g}{\partial x\partial y} + y^2\frac{\partial^2 g}{\partial y^2} = 1,

化简得

u^2f''(u) + uf'(u) = 1,

即

f''(u) + \frac{1}{u}f'(u) = \frac{1}{u^2}.

令 $p = f'(u)$ ，则

p' + \frac{1}{u}p = \frac{1}{u^2}.

解得

p = e^{-\int \frac{1}{u}du}\left[\int \frac{1}{u^2}e^{\int \frac{1}{u}du}du + C\right] = \frac{1}{u}\left[\int \frac{1}{u}du + C\right] = \frac{\ln u}{u} + \frac{C}{u}.

由 $p|_{u=1} = C = 2$ ，得

p = \frac{\ln u}{u} + \frac{2}{u}.

因此

\frac{df}{du} = \frac{\ln u}{u} + \frac{2}{u},

积分得

f(u) = \int \left(\frac{\ln u}{u} + \frac{2}{u}\right)du = \frac{1}{2}\ln^2 u + 2\ln u + C.

由 $f(1) = C = 1$ ，得

f(u) = \frac{1}{2}\ln^2 u + 2\ln u + 1.

19

（本题满分12分）

设函数 $f(x)$ 在区间 $(a,b)$ 内可导.证明导函数 $f'(x)$ 在 $(a,b)$ 内严格单调增加的充分必要条件是:对 $(a,b)$ 内任意的 $x_1,x_2,x_3$ ，当 $x_1\lt x_2\lt x_3$ 时 $\frac{f(x_2) - f(x_1)}{x_2 - x_1}\lt\frac{f(x_3) - f(x_2)}{x_3 - x_2}$ .

高等数学一元函数微分学导数的几何意义

【答案】 见解析

【解析】 充分性：若对 $(a,b)$ 内任意的 $x_1,x_2,x_3$ ，当 $x_1\lt x_2\lt x_3$ 时，都有

\frac{f(x_2) - f(x_1)}{x_2 - x_1}\lt\frac{f(x_3) - f(x_2)}{x_3 - x_2}

则在 $(a,b)$ 内取任意的 $x_1\lt x_2\lt x_3\lt x_4\lt x_5$ ，有

\frac{f(x_2) - f(x_1)}{x_2 - x_1}\lt\frac{f(x_3) - f(x_2)}{x_3 - x_2}\lt\frac{f(x_4) - f(x_3)}{x_4 - x_3}\lt\frac{f(x_5) - f(x_4)}{x_5 - x_4}

在 $\frac{f(x_2) - f(x_1)}{x_2 - x_1}\lt\frac{f(x_3) - f(x_2)}{x_3 - x_2}$ 两边同时令 $x_2 \to x_1^+$ ，得

f_+'(x_1)\leq\frac{f(x_3) - f(x_1)}{x_3 - x_1}

两边同时令 $x_2 \to x_3^-$ ，得 $\frac{f(x_3) - f(x_1)}{x_3 - x_1}\leq f_-'(x_3)$ ，即

f_+'(x_1)\leq\frac{f(x_3) - f(x_1)}{x_3 - x_1}\leq f_-'(x_3)

同理可得 $f_+'(x_3)\leq\frac{f(x_3) - f(x_1)}{x_3 - x_1}\leq f_-'(x_5)$ .因为

\frac{f(x_3) - f(x_1)}{x_3 - x_1}\lt\frac{f(x_5) - f(x_3)}{x_5 - x_3}

所以 $f_+'(x_1)\leq f_-'(x_5)$ .由 $x_1,x_5$ 的任意性，可得 $f'(x)$ 在 $(a,b)$ 内严格单调递增，充分性得证。

再证必要性，即已知 $f'(x)$ 单调递增，在 $[x_1,x_2],[x_2,x_3]$ 上分别使用拉格朗日中值定理，知存在 $\xi_1 \in (x_1,x_2),\xi_2 \in (x_2,x_3)$ ，使

f'(\xi_1)=\frac{f(x_2) - f(x_1)}{x_2 - x_1}, \quad f'(\xi_2)=\frac{f(x_3) - f(x_2)}{x_3 - x_2}

又由 $f'(x)$ 单调递增，且 $\xi_1\lt\xi_2$ 知， $f'(\xi_1)\lt f'(\xi_2)$ ，即

\frac{f(x_2) - f(x_1)}{x_2 - x_1}\lt\frac{f(x_3) - f(x_2)}{x_3 - x_2}

必要性得证。

综上所述，充要条件得证。

20

（本题满分 12 分）

设 $\varSigma$ 是由直线 $\begin{cases} x = 0 \\ y = 0 \end{cases}$ 绕直线 $\begin{cases} x = t \\ y = t \\ z = t \end{cases}$ （ $t$ 为参数）旋转一周得到的曲面， $\varSigma_1$ 是 $\varSigma$ 介于平面 $x + y + z = 0$ 与平面 $x + y + z = 1$ 之间部分的外侧，计算曲面积分

I = \iint\limits_{\varSigma_1} x \, \mathrm{d}y \, \mathrm{d}z + (y + 1) \, \mathrm{d}z \, \mathrm{d}x + (z + 2) \, \mathrm{d}x \, \mathrm{d}y

高等数学多元函数积分学第二类曲面积分

【答案】 $I = \frac{\sqrt{2}}{4} \pi - 1$

由题意可知，直线 $\begin{cases} x = 0 \\ y = 0 \end{cases}$ 记为 $l_1$ ；直线 $\begin{cases} x = t \\ y = t \\ z = t \end{cases}$ 记为 $l_2$ 。

则直线 $l_1$ 绕直线 $l_2$ 旋转所得曲面 $\varSigma$ 为 $(x - t)^2 + (y - t)^2 + (z - t)^2 = 3t^2$ 。

已知 $\varSigma_1$ 是 $\varSigma$ 介于平面 $x + y + z = 0$ 和平面 $x + y + z = 1$ 之间的外侧，则补面 $\varSigma_0: x + y + z = 1$ ，方向指向外侧。
则 $\varSigma_0$ 与 $\varSigma_1$ 所围为封闭区域，由高斯公式可知

I_1 = \oiint_{\Sigma_0 + \Sigma_1} x \, dy \, dz + (y + 1) \, dz \, dx + (z + 2) \, dx \, dy

上面闭合曲面积分无法正常显示，见下图

= \iiint_{\varOmega} (1 + 1 + 1) \, dv = 3 \iiint_{\varOmega} dv = 3 \cdot \frac{1}{3} \pi \left( \frac{\sqrt{2}}{2} \right)^2 \left( \frac{\sqrt{2}}{2} \right) = \frac{\sqrt{2}}{4} \pi

（注： $\varOmega$ 为圆锥体）。

记 $D_{xy}$ 为 $\varSigma_0$ 在 $xOy$ 面上的投影，

D_{xy} = \left\{ (x, y) \vert 0 \leqslant x + y \leqslant 1, \, x \geqslant 0, \, y \geqslant 0 \right\}

又

\begin{align*} I_2 &= \iint_{\varSigma_0} x \, dy \, dz + (y + 1) \, dz \, dx + (z + 2) \, dx \, dy \\ &= \iint_{D_{xy}} x \, dx \, dy + (y + 1) \, dx \, dy + (3 - x - y) \, dx \, dy \\ &= \iint_{D_{xy}} 2 \, dx \, dy = 2 \cdot \frac{1}{2} \cdot 1 \cdot 1 = 1 \end{align*}

故

I = I_1 - I_2 = \frac{\sqrt{2}}{4} \pi - 1

21

（本题满分 12 分）设矩阵 $A = \begin{pmatrix} 0 & -1 & 2 \\ -1 & 0 & 2 \\ -1 & -1 & a \end{pmatrix}$ ，已知 $1$ 是 $A$ 的特征多项式的重根。

(1) 求 $a$ 的值；

(2) 求所有满足 $A\alpha = \alpha + \beta$ ， $A^{2}\alpha = \alpha + 2\beta$ 的非零列向量 $\alpha$ ， $\beta$ 。

线性代数矩阵的特征值与特征向量

【答案】
(1) $a = 3$
(2) 设 $\alpha = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}$ ，其中 $a_1, a_2, a_3$ 满足 $a_1 a_2 a_3 \neq 0$ 且 $a_1 + a_2 \neq 2a_3$ ，则 $\beta = \begin{pmatrix} 2a_3 - a_1 - a_2 \\ 2a_3 - a_1 - a_2 \\ 2a_3 - a_1 - a_2 \end{pmatrix}$ .

【解析】
（1）
由

f(\lambda) = |A - \lambda E| = (1 - \lambda)\big[(\lambda - a)(\lambda + 1) + 4\big],

代入 $\lambda = 1$ 得

\begin{gather*} (1 - a)(1 + 1) + 4 = 0, \\ a = 3. \end{gather*}

（2）
由（1）可知

A = \begin{pmatrix} 0 & -1 & 2 \\ -1 & 0 & 2 \\ -1 & -1 & 3 \end{pmatrix}.

由 $|A - \lambda E| = 0$ ，得 $A$ 的特征值 $\lambda_1 = \lambda_2 = \lambda_3 = 1$ 。

已知

A\alpha = \alpha + \beta, \quad A^2\alpha = \alpha + 2\beta,

则

\begin{gather*} (A - E)\alpha = \beta, \\ (A^2 - E)\alpha = 2\beta = 2(A - E)\alpha, \\ (A - E)^2\alpha = 0, \\ (A - E)^2 = 0. \end{gather*}

故 $\alpha$ 可取任意非零向量。设

\alpha = (a_1, a_2, a_3)^{\mathrm{T}}, \quad a_1a_2a_3 \neq 0.

于是

\beta = (A - E)\alpha = \begin{pmatrix} -1 & -1 & 2 \\ -1 & -1 & 2 \\ -1 & -1 & 2 \end{pmatrix} \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} = \begin{pmatrix} 2a_3 - a_1 - a_2 \\ 2a_3 - a_1 - a_2 \\ 2a_3 - a_1 - a_2 \end{pmatrix},

其中 $a_1 + a_2 \neq 2a_3$ 。

综上，

\alpha = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \quad \beta = \begin{pmatrix} 2a_3 - a_1 - a_2 \\ 2a_3 - a_1 - a_2 \\ 2a_3 - a_1 - a_2 \end{pmatrix},

满足 $a_1a_2a_3 \neq 0$ 且 $a_1 + a_2 \neq 2a_3$ 。

22

（本题满分 12 分）

投保人的损失事件发生时，保险公司的赔付额 $Y$ 与投保人的损失额 $X$ 的关系为

Y = \begin{cases} 0, & X \leq 100, \\ X - 100, & X > 100. \end{cases}

设定损事件发生时，投保人的损失额 $X$ 的概率密度为

f(x) = \begin{cases} \dfrac{2 \times 100^2}{(100 + x)^3}, & x > 0, \\ 0, & x \leq 0. \end{cases}

（1）求 $P\{Y > 0\}$ 及 $EY$ 。

（2）这种损失事件在一年内发生的次数记为 $N$ ，保险公司在一年内就这种损失事件产生的理赔次数记为 $M$ ，假设 $N$ 服从参数为 $8$ 的泊松分布，在 $N = n$ （ $n \geq 1$ ）的条件下， $M$ 服从二项分布 $B(n, p)$ ，其中 $p = P\{Y > 0\}$ ，求 $M$ 的概率分布。

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

【答案】
(1) $P\{Y > 0\} = \frac{1}{4}$ ， $EY = 50$
(2) $M \sim P(2)$ ，即 $P\{M = m\} = \frac{2^m}{m!} e^{-2}$

【解析】
(1)

P\{Y > 0\} = P\{X - 100 > 0\} = P\{X > 100\} = \int_{100}^{+\infty} \frac{2 \times 100^2}{(100 + x)^3} \, dx = \frac{1}{4}

EY = \int_{100}^{+\infty} (x - 100) \frac{2 \times 100^2}{(100 + x)^3} \, dx = 50

(2)

N \sim P(8),\quad \{M \mid N = n\} \sim B\left(n, \frac{1}{4}\right)

\begin{align*} P\{M = m\} &= \sum_{n = m}^{\infty} P\{N = n\} \cdot P\{M = m \mid N = n\} \\ &= \sum_{n = m}^{\infty} \frac{8^n}{n!} e^{-8} \cdot C_n^m \cdot \left(\frac{1}{4}\right)^m \cdot \left(\frac{3}{4}\right)^{n - m} \\ &= \sum_{n = m}^{\infty} \frac{8^n}{n!} e^{-8} \cdot \frac{n!}{m!(n - m)!} \left(\frac{1}{4}\right)^m \cdot \left(\frac{3}{4}\right)^{n - m} \\ &= \left(\frac{1}{4}\right)^m e^{-8} \frac{8^m}{m!} \sum_{n = m}^{\infty} \frac{8^{n - m}}{(n - m)!} \cdot \left(\frac{3}{4}\right)^{n - m} \\ &= \left(\frac{1}{4}\right)^m e^{-8} \frac{8^m}{m!} \sum_{n = m}^{\infty} \frac{6^{n - m}}{(n - m)!} = \frac{2^m}{m!} e^{-2} \end{align*}