2008 年真题
选择题
1
设函数
f(x)=x2(x−1)(x−2)
,求
f′(x)
的零点个数为
正确答案:D命题目的
考查求导的运算能力。
详细解答
函数
f(x)=2x(x−1)(x−2)+x2(x−2)+x2(x−1)
。
整理得
f(x)=4x3−9x2+4x
。
求导得
f′(x)=12x2−18x+4
。
令
f′(x)=0
,即解方程
12x2−18x+4=0
。
判别式
Δ=(−18)2−4×12×4=324−192=132>0
,
故该方程有两个不同实根,因此
f′(x)
的零点个数为 2。
易错辨析
对于二次方程
ax2+bx+c=0
,当
b2−4ac>0
时,方程有两个不同实根。
延伸拓展
n 次方程在复数范围内有 n 个根(包括重根)。
2
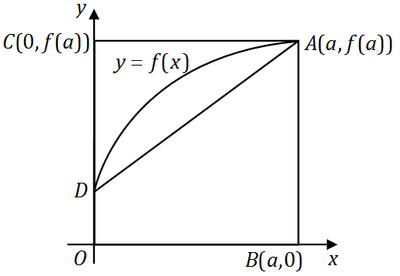
如图,曲线段的方程为
y=f(x)
,函数
f(x)
在区间
[0,a]
上有连续的导数,则定积分
∫0axf′(x)dx
等于( )
正确答案:C命题目的
考查定积分的分部积分法及定积分的几何意义。
详细解答
∫0axf′(x)dx=∫0axdf(x)=af(a)−∫0af(x)dx
其中
af(a)
表示矩形面积,
∫0af(x)dx
表示曲边梯形的面积,因此
∫0axf′(x)dx
表示曲边三角形的面积。
易错辨析
若
f(x)≤0
,则曲边梯形的面积为:
−∫0af(x)dx
延伸拓展
必须熟练掌握定积分的分部积分法及变量替换法。
3
在下列微分方程中,以
y=C1ex+C2cos2x+C3sin2x
(
C1
、
C2
、
C3
为任意常数)为通解的是( )
正确答案:D【命题目的】
考查高阶齐次常系数微分方程的解法。
【详细解答】
由
y=C1ex+C2cos2x+C3sin2x
可知其特征根为
λ1=1,λ2,3=±2i
特征方程为:
(λ−1)(λ+2i)(λ−2i)=(λ−1)(λ2+4)
即
λ3−λ2+4λ−4=0
所以所求微分方程为:
y′′′−y′′+4y′−4y=0
故选 (D)。
【易错辨析】
C2cos2x+C3sin2x
对应的特征方程为
(λ+2i)(λ−2i)=λ2+4
【延伸拓展】
高阶齐次常系数微分方程的解法见同济大学《高等数学》第五版下册。
4
设函数
f(x)=∣x−1∣ln∣x∣sinx
,则
f(x)
有(
正确答案:A命题目的
考查函数间断点及其类型。
详细解答
函数
f(x)
的间断点为
x=0
和
x=1
。
计算极限得:
x→0+limf(x)=0
因此
x=0
是可去间断点。
又:
x→1+limf(x)=sin1,x→1−limf(x)=−sin1
左右极限存在但不相等,因此
x=1
是跳跃间断点。
故应选 (A)。
延伸拓展
在点
x
处可导一定连续,但连续不一定可导。
5
设函数
f(x)
在
(−∞,+∞)
内单调有界,
{xn}
为数列,下列命题正确的是( )
正确答案:B命题目的
考查定理:单调有界数列一定有极限。
详细解答
若
xn
单调,则由
f(x)
在
(−∞,+∞)
内单调有界,可知
f(xn)
单调有界,因此
f(xn)
收敛,故应选 (B)。
延伸拓展
“单调有界数列一定有极限”具体表述为:
- 单增有上界数列一定有极限;
- 单减有下界数列一定有极限。
6
设函数
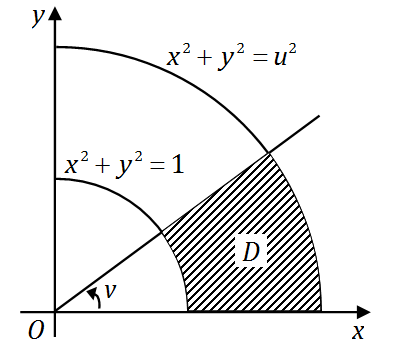
F(u,v)=∬Duvx2+y2f(x2+y2)dxdy
,其中区域
Duv
为如图中阴影部分,则
∂u∂F=()
。
正确答案:A[命题目的]考查二重积分的极坐标变换及求偏导数和对定积分上限变量求导。
[详细解答]用极坐标得
F(u,v)=∫0vdθ∫1urf(r2)⋅rdr=v∫1uf(r2)dr,
因此
∂u∂F=vf(u2).
7
设
A
为
n
阶非零矩阵,
E
为
n
阶单位矩阵,若
A3=O
,则( )
正确答案:C命题目的
考查逆矩阵的概念。
详细解答
方法一
由已知
A3=0
,可得
(E−A)(E+A+A2)=E−A3=E,
(E+A)(E−A+A2)=E+A3=E.
因此
E−A
与
E+A
均可逆。
方法二
设
A
的特征值为
λ
,由
A3=0
可得
λ3=0
,从而
λ=0
。
于是
E−A
与
E+A
的特征值均为 1,因此
∣E−A∣=1,∣E+A∣=1,
故
E−A
与
E+A
均可逆。
易错辨析
由
A3=0
不能推出
A=0
。
延伸拓展
- 矩阵
A
可逆的充要条件:
- 存在矩阵
B
满足
AB=BA=E
;
- 存在矩阵
B
满足
AB=E
或
BA=E
;
- ∣A∣=0
;
- A
的所有特征值不等于 0;
- r(A)=n
。
- 设
A
的特征值为
λ
,则多项式
Pn(A)
的特征值为
Pn(λ)
。
8
设
A=(1221)
,则在实数域上与
A
合同的矩阵为( )
正确答案:D【命题目的】考查两个矩阵合同的概念。
【详细解答】
方法一:计算特征值。
∣λE−A∣=λ−1−2−2λ−1=(λ−1)2−4=λ2−2λ−3=(λ+1)(λ−3)=0 因此
λ1=−1
,
λ2=3
。
记
D=(1−2−21)
,则
∣λE−D∣=λ−122λ−1=(λ−1)2−4=λ2−2λ−3=(λ+1)(λ−3)=0 因此
λ1=−1
,
λ2=3
。
方法二:利用行列式与特征值的关系。
说明
A
的特征值一正一负。
对于
D
:
说明
D
的特征值也为一正一负。
A
与
D
的正负惯性指数相同,因此应选 (D)。
【易错辨析】方法二仅适用于本题(读者可自行思考原因)。
【延伸拓展】两个矩阵的等价、相似、合同概念存在不同之处。
填空题
9
(填空题)已知函数
f(x)
连续,且
x→0lim(ex2−1)f(x)1−cos[xf(x)]=1,
则
f(0)=
【答案】 2
【解析】 本题旨在考查
00
型未定式的极限计算。
已知极限
x→0limx2f(x)21x2f2(x)=1
化简可得
x→0limf(x)21f2(x)=1
由于
f(x)
在
x→0
时非零,可约去
f(x)
,得
x→0lim21f(x)=1
因此
21f(0)=1
解得
f(0)=2
易错辨析:在极限运算中,对于加减项不能随意使用等价无穷小代换,否则可能导致结果错误。
10
(填空题)微分方程
(y+x2e−x)dx−xdy=0
的通解是
y=
【答案】
y=−xe−x+Cx
【解析】 ## 题目
(填空题)微分方程
(y+x2e−x)dx−xdy=0
的通解是
y=
解析
命题目的考查求解一阶线性微分方程。
详细解答将方程整理为
y′−xy=xe−x
,
其中
P=−x1
,
Q=xe−x
。
利用一阶线性微分方程通解公式:
y=e∫x1dx(∫xe−xe∫x1dxdx+C)=x(∫e−xdx+C)=−xe−x+Cx
延伸拓展:
- 也可用常数变易法求解一阶线性微分方程;
- 一阶线性微分方程通解 = 齐次方程通解 + 非齐次方程特解。
11
(填空题)曲线
sin(xy)+ln(y−x)=x
在点
(0,1)
处的切线方程是
【答案】
y=x+1
【解析】 命题目的:考查隐函数求导及导数的几何意义。
详细解答
方法一:设
F(x,y)=sin(xy)+ln(y−x)−x,
计算
k=−FyFx=−xcos(xy)+y−x1ycos(xy)+y−x−1−1.
代入
x=0
,
y=1
,得
k=1
,切线方程为
y=x+1
。
方法二:方程两边对
x
求导,
cos(xy)⋅(y+xy′)+y−xy′−1=1,
令
x=0
,
y=1
,得
k=y′(0)=1
,切线方程为
y=x+1
。
易错辨析:
sin(xy)
对
x
求导时,
y
是中间变量。计算时不必求出
y′
的表达式,直接代入
x=0
,
y=1
即可得出
k=1
。
延伸拓展:只要不对自变量
x
求导,都要按照复合函数求导。
12
(填空题)曲线
y=(x−5)x32
的拐点坐标为 ______
【答案】
(−1,−6)
【解析】 命题目的考查拐点的概念。
详细解答计算
f′(x)=x32+(x−5)⋅32x−31=35(x−2)x−31
,再求二阶导数
f′′(x)=910x−34(x+1)
,令其为零得
x=−1
。
当
x=−1
时,
f′′(x)
左右两边符号改变,故拐点坐标为
(−1,−6)
。
当
x=0
时,二阶导数不存在,且
f′′(x)
左右两边符号不变,故
(0,0)
不是拐点。
易错辨析
- 如果在
(0,0)
两侧
f′′(x)
符号改变,则
(0,0)
也是拐点;
- 拐点应表示为
(x0,f(x0))
。
延伸拓展
如果在
(x0,f(x0))
两侧
f′′(x)
符号改变,则
(x0,f(x0))
是拐点。
13
(填空题)设
z=(xy)yx
,则
∂x∂z(1,2)=
【答案】
22(ln2−1)
【解析】
命题目的考查多元函数的复合函数求导。
详细解答
方法一:令
u=xy
,
v=yx
,则
z=uv
。取对数后对
x
求导,可得:
z1∂x∂z=y1lnxy−y1
代入点
(1,2)
得:
方法二:直接取对数后对
x
求导,代入
(1,2,2)
得:
易错辨析:方法二比方法一运算量小,不易出错。
延伸拓展:本题也可求全微分:
dz=∂x∂zdx+∂y∂zdy
14
(填空题)设 3 阶矩阵
A
的特征值为
2
、
3
、
λ
。若行列式
∣2A∣=−48
,则
λ=
【答案】
λ=−1
【解析】 命题目的考查
∣A∣=λ1λ2⋯λn
与
∣kA∣=kn∣A∣
。
详细解答如下:由
∣2A∣=23∣A∣=−48
,得
∣A∣=−6
。又因为
∣A∣=2×3×λ=−6
,故
λ=−1
。
易错辨析:常见错误是误以为
∣2A∣=2∣A∣=−48
,正确应为
∣2A∣=23∣A∣
。
延伸拓展:假设
A
的特征值为
λ
,则
A
的多项式
Pn(A)
的特征值为
Pn(λ)
。
解答题
15
(本题满分 10 分)求极限
x→0limx4[sinx−sin(sinx)]sinx
【答案】
61
【解析】
x→0limx4[sinx−sin(sinx)]sinx=x→0limx3sinx−sin(sinx)=x→0lim3x2cosx−cos(sinx)⋅cosx=x→0lim3x2cosx[1−cos(sinx)]=x→0lim3x221sin2x⋅cosx=61.
[命题目的] 考查
00
型极限的计算。
[思路点拨] 先使用等价无穷小代换,然后使用洛必达法则。
[易错辨析] 对于加、减项不能使用等价无穷小代换。
[延伸拓展] “
00
”、“
1∞
”等其他不定型的极限的求法。
16
(本题满分 10 分)设函数
y=y(x)
由参数方程
{x=x(t),y=∫0t2ln(1+u)du
确定,其中
x(t)
满足微分方程
dtdx−2te−x=0
且
x∣t=0=0
,求
dx2d2y
。
【答案】 \[\frac{d^{2}y}{dx^{2}} = (1 + t^{2})\left[\ln(1 + t^{2}) + 1\right] \]
【解析】
[详细解答]
已知
exdx=2tdt
,积分得
ex=t2+C
。由
x∣t=0=0
得
C=1
,故
x=ln(1+t2)
。
dxdy=xt′yt′=1+t22t2tln(1+t2)=(1+t2)ln(1+t2)
dx2d2y=xt′[(1+t2)ln(1+t2)]′=1+t22t2tln(1+t2)+2t=(1+t2)[ln(1+t2)+1]
[命题目的]
考查求微分方程特解和参数方程求导。
[思路点拨]
- 对
x
和
t
,为可分离变量方程;
- 求导过程中,
t
是中间变量。
[延伸拓展]
可用相同方法求三阶导数。
17
(本题满分 10 分)计算
【答案】
41+16π2
【解析】
命题目的
考查定积分的变量替换。
思路点拨
对含
a2−x2
类型的积分,令
x=asint
。
详细解答
令
x=sint
,则
∫011−x2x2arcsinxdx=∫02πcostsin2t⋅tcostdt=∫02πtsin2tdt=21∫02πtdt−21∫02πtcos2tdt=41+16π2 易错辨析
定积分变量替换一定要改变上下限。
延伸拓展
对含
a2+x2
类型的积分,令
x=atant
。
18
(本题满分 10 分)
计算
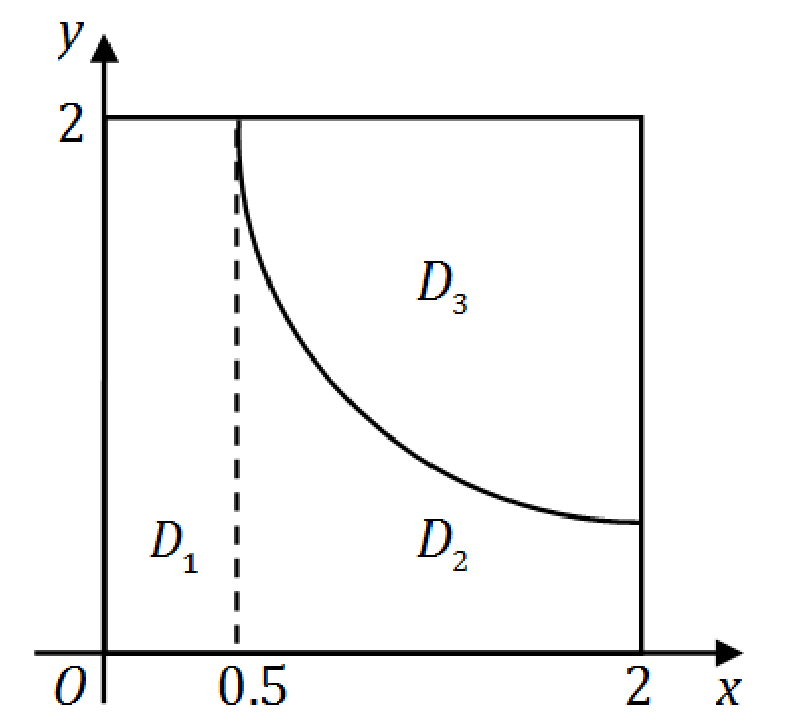
∬Dmax{xy,1}dxdy,
其中
D={(x,y)∣0≤x≤2,0≤y≤2}.
【答案】
419+ln2
【解析】
曲线
xy=1
将区域分成三个区域
D1,D2,D3
:
从而所求的积分
∬Dmax(xy,1)dxdy=∬D1xydxdy+∬D21dxdy+∬D31dxdy=∫021dx∫021dy+∫212dx∫0x11dy∫212dx∫x12xydy=1+2ln2+415−ln2=419+ln2.
19
(本题满分 10 分)设
f(x)
是区间
[0,+∞)
上具有连续导数的单调增加函数,且
f(0)=1
。对任意的
t∈[0,+∞)
,直线
x=0
,
x=t
,曲线
y=f(x)
以及
x
轴所围成的曲边梯形绕
x
轴旋转一周生成一旋转体。若该旋转体的侧面面积在数值上等于其体积的 2 倍,求函数
f(x)
的表达式。
【答案】
f(x)=coshx
【解析】 ## 解析
旋转体的体积公式为:
V(t)=π∫0t[f(x)]2dx
旋转体的侧面积公式为:
S(t)=2π∫0tf(x)1+[f′(x)]2dx 由题意可知
S(t)=2V(t)
,即:
2π∫0tf(x)1+[f′(x)]2dx=2π∫0t[f(x)]2dx 两边对
t
求导,得到:
化简得:
两边平方得:
1+[f′(t)]2=[f(t)]2
整理得:
[f′(t)]2=[f(t)]2−1
由于
f(x)
单调增加,因此:
分离变量得:
积分得:
由初始条件
f(0)=1
,代入得
C=0
,因此:
解得:
f(x)=2ex+e−x=coshx
[命题目的] 考查旋转体侧面积、体积计算及微分方程的综合应用。
[思路点拨] 由
V(t)S(t)=2
对上限变量求导得到微分方程。
20
(本题满分 11 分)
(I) 证明积分中值定理:若函数
f(x)
在闭区间
[a,b]
上连续,则至少存在一点
η∈[a,b]
,使得
∫abf(x)dx=f(η)(b−a)
(II) 若函数
φ(x)
具有二阶导数,且满足
φ(2)>φ(1)
及
φ(2)>∫23φ(x)dx
,则至少存在一点
ξ∈(1,3)
,使得
φ′′(ξ)<0
【答案】 见解析
【解析】 设
M
及
m
分别是函数
f(x)
在区间
[a,b]
上的最大值及最小值,则
m(b−a)≤∫abf(x)dx≤M(b−a)
将不等式两边除以
b−a
,得
m≤b−a1∫abf(x)dx≤M
根据闭区间上连续函数的介值定理,在
[a,b]
上至少存在一点
η
,使得
f(η)=b−a1∫abf(x)dx
即
∫abf(x)dx=f(η)(b−a)
由积分中值定理,存在
c∈(2,3)
,使得
∫23φ(x)dx=φ(c)
由题设
φ(2)>φ(1)
且
φ(2)>φ(c)
。
对
φ(x)
在区间
[1,2]
和
[2,c]
上分别应用拉格朗日中值定理,得
φ′(ξ1)=2−1φ(2)−φ(1)>0,ξ1∈(1,2)
φ′(ξ2)=c−2φ(c)−φ(2)<0,ξ2∈(2,c)
再对
φ′(x)
在区间
[ξ1,ξ2]
上应用拉格朗日中值定理,存在
ξ∈(ξ1,ξ2)⊂(1,3)
使得
φ′′(ξ)=ξ2−ξ1φ′(ξ2)−φ′(ξ1)<0
[命题目的] 考查积分中值定理证明及导数应用。
[思路点拨] 第一问的结果是解答第二问的关键。
[易错辨析] 连续函数的介值定理中
η
在闭区间
[a,b]
上。
[延伸拓展] 改进后的积分中值定理中
ξ
可在开区间
(a,b)
上。
21
(本题满分 11 分)求函数
u=x2+y2+z2
在约束条件
z=x2+y2
和
x+y+z=4
下的最大值与最小值。
【答案】 最大值 72,最小值 6
【解析】
命题目的
考查条件极值的拉格朗日乘数法。
思路点拨
求解具有两个约束条件的条件极值,方法与单一约束条件的情形相同。
详细解答
设
F(x,y,z)=x2+y2+z2+λ1(x2+y2−z)+λ2(x+y+z−4)
得到方程组
⎩⎨⎧Fx=0Fy=0Fz=0x2+y2−z=0x+y+z−4=0 即
⎩⎨⎧2x+2xλ1+λ2=02y+2yλ1+λ2=02z−λ1+λ2=0x2+y2−z=0x+y+z−4=0 解得
⎩⎨⎧x=−2y=−2z=8或⎩⎨⎧x=1y=1z=2 于是
Umax=(−2)2+(−2)2+82=72
Umin=12+12+22=6
易错辨析
求解方程组是最容易出错的地方,计算时应仔细。
延伸拓展
可进一步探讨具有更多约束条件的最值问题。
22
(本题满分 11 分)设
n
元线性方程组
Ax=b
,其中
A=2aa212aa212a⋱1⋱a2⋱2aa212an×n,x=x1x2⋮xn,b=10⋮0 (I)证明行列式
∣A∣=(n+1)an
(II)当
a
为何值时,该方程组有唯一解,并求
x1
(III)当
a
为何值时,该方程组有无穷多解,并求通解。
【答案】
(I) 见解析
(II) 当
a=0
时,方程组有唯一解,且
x1=(n+1)an
(III) 当
a=0
时,方程组有无穷多解,且通解为
x=k100⋮0+010⋮0
,其中
k
为任意常数。
【解析】
命题目的
计算 n 阶三对角线行列式、求解非齐次方程组。
思路点拨
非齐次方程组的通解 = 齐次方程组的通解 + 非齐次方程组的特解。
详细解答
(I)
∣A∣=2aa212a⋱⋱⋱⋱⋱⋱a212a=(n+1)an. 另一种方法(递推法):
Dn=∣A∣=2aa212aa212a⋱⋱⋱⋱⋱⋱a212a=2aDn−1−a2Dn−2. 直接计算得:
D1=2a=(1+1)a1
,
D2=3a2=(2+1)a2
,
假设
Dn−1=nan−1
,则
Dn=2aDn−1−a2Dn−2=2a⋅nan−1−a2⋅(n−1)an−2=(2n−n+1)an=(n+1)an.
(II)
方程组有唯一解时,由
Ax=B
知
∣A∣=0
,又
∣A∣=(n+1)an
,故
a=0
。
记
A=An×n
,由克莱姆法则知,
x1=∣A∣∣A1∣,
其中
A1
是将
A
的第一列替换为
b
后的行列式。经计算可得
x1=(n+1)annan−1=(n+1)an.
(III)
方程组有无穷多解时,
∣A∣=0
,即
a=0
。此时
(A∣B)=00⋮010⋮001⋮0⋯⋯⋱⋯10⋮0. 对应的齐次方程组
Ax=0
的基础解系为
ξ=(1,0,0,…,0)T,
非齐次方程组的一个特解为
η=(0,1,0,…,0)T,
故通解为
x=k(1,0,0,…,0)T+(0,1,0,…,0)T,
其中
k
为任意常数。
易错辨析
用递推法计算
∣A∣
的值比使用行列式性质计算,运算量要小得多。
23
(本题满分 11 分)设
A
为 3 阶矩阵,
α1
、
α2
为
A
的分别属于特征值
−1
、
1
的特征向量,向量
α3
满足
Aα3=α2+α3
。
(I) 证明
α1
、
α2
、
α3
线性无关;
(II) 令
P=(α1,α2,α3)
,求
P−1AP
。
【答案】
(I) 见解析
(II)
−100010011
【解析】
命题目的
考查向量的线性相关性。
思路点拨
使用线性相关和线性无关的定义进行证明。
详细解答
(I) 方法一
假设
α1,α2,α3
线性相关。因为
α1,α2
是不同特征值的特征向量,所以线性无关,则
α3
可由
α1,α2
线性表出。不妨设
α3=l1α1+l2α2
,其中
l1,l2
不全为零(若
l1,l2
同时为 0,则
α3=0
,由
Aα3=α2+α3
可知
α2=0
)。
由于
Aα1=−α1
,
Aα2=α2
,可得
Aα3=α2+α3=α2+l1α1+l2α2,
又
Aα3=A(l1α1+l2α2)=−l1α1+l2α2,−l1α1+l2α2=α2+l1α1+l2α2,2l1α1+α2=0.
则
α1,α2
线性相关,矛盾(因为
α1,α2
分别属于不同特征值的特征向量,故线性无关)。所以
α1,α2,α3
线性无关。
方法二
因为
α1,α2
是不同特征值的特征向量,所以线性无关。假设
k1α1+k2α2+k3α3=0(1),k1Aα1+k2Aα2+k3Aα3=0,−k1α1+k2α2+k3(α2+α3)=0(2).
(1) − (2) 得
2k1α1−k3α2=0,
所以
k1=k3=0
,代入 (1) 得
k2α2=0
,故
k2=0
。因此
α1,α2,α3
线性无关。
(II)
记
P=(α1,α2,α3)
,则
P
可逆。
A(α1,α2,α3)=(Aα1,Aα2,Aα3)=(−α1,α2,α2+α3)=(α1,α2,α3)
即
所以
易辨析
以下说法是错误的:线性相关,则任一向量可用其他向量线性表示。
正确说法是:
α1,α2,…,αn
线性相关,则其中某一向量可用其他向量线性表示。