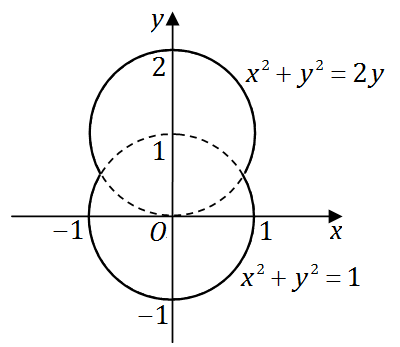2011 年真题

选择题

1

已知当 $x \to 0$ 时，函数 $f(x) = 3 \sin x - \sin 3x$ 与 $c x^{k}$ 是等价无穷小，则（

正确答案：C

根据泰勒公式及无穷小阶的比较可得。

\sin x = x - \frac{x^{3}}{3!} + o\left(x^{3}\right), \quad \sin 3x = 3x - \frac{27x^{3}}{3!} + o\left(x^{3}\right)

\lim_{x \to 0} \frac{3 \sin x - \sin 3x}{c x^{k}} = \lim_{x \to 0} \frac{-\frac{x^{3}}{2} + \frac{9x^{3}}{2} + o\left(x^{3}\right)}{c x^{k}} = \lim_{x \to 0} \frac{4x^{3}}{c x^{k}} = 1

因此 $c = 4$ ， $k = 3$ 。

\begin{aligned} \lim_{x \to 0} \frac{3 \sin x - \sin 3x}{c x^{k}} &= \lim_{x \to 0} \frac{3 \cos x - 3 \cos 3x}{c k x^{k-1}} = \lim_{x \to 0} \frac{3}{c k} \cdot \frac{-2 \sin 2x \sin (-x)}{x^{k-1}} \\ &= \frac{12}{c k} \lim_{x \to 0} \frac{x^{2}}{x^{k-1}} = 1 \end{aligned}

所以 $k - 1 = 2$ ， $c k = 12$ ，即 $k = 3$ ， $c = 4$ 。

2

已知 $f(x)$ 在 $x = 0$ 处可导，且 $f(0) = 0$ ，则

\lim_{x \to 0} \frac{x^2 f(x) - 2f(x^3)}{x^3}

等于（）

高等数学一元函数微分学导数与微分的概念

正确答案：B

根据导数在某点的定义求解。

\lim _{x \to 0} \frac{x^{2} f(x)-2 f\left(x^{3}\right)}{x^{3}}=\lim _{x \to 0} \frac{x^{2} f(x)-x^{2} f(0)}{x^{3}}-\lim _{x \to 0} \frac{2 f\left(x^{3}\right)-2 f(0)}{x^{3}}

= f^{\prime}(0)-2 f^{\prime}(0) = -f^{\prime}(0)

3

函数 $f(x) = \ln |(x-1)(x-2)(x-3)|$ 的驻点个数为（）

高等数学一元函数微分学函数的单调性、极值与最值

正确答案：C
函数的一阶导数为零的点为驻点，即

f'(x) = 0

的解为

x = 2 \pm \frac{1}{\sqrt{3}}

。

4

微分方程 $y^{\prime \prime} - \lambda^{2} y = e^{\lambda x} + e^{-\lambda x} (\lambda > 0)$ 的特解形式为

高等数学常微分方程常系数非齐次线性微分方程

正确答案：C

当特征值为 $\pm \lambda$ ，且非齐次项中 $\pm \lambda$ 分别与特征根相等时，特解可设为：

x\left(a e^{\lambda x} + b e^{-\lambda x}\right)

5

设函数 $f(x)$ 、 $g(x)$ 均有二阶连续导数，满足 $f(0) > 0$ 、 $g(0) < 0$ ，且 $f'(0) = g'(0) = 0$ ，则函数 $z = f(x) g(y)$ 在点 $(0, 0)$ 处取得极小值的一个充分条件是（）

高等数学多元函数微分学多元函数的极值问题

正确答案：A

根据

\begin{aligned} z_x &= f'(x) g(y) = 0, \\ z_y &= f(x) g'(y) = 0 \end{aligned}

以及

z_{xx} = f''(x) g(y), \quad z_{yy} = f(x) g''(y), \quad z_{xy} = f'(x) g'(y),

对于点 $(0,0)$ ，有

z_{xx}(0,0) = f''(0) g(0), \quad z_{yy}(0,0) = f(0) g''(0), \quad z_{xy}(0,0) = f'(0) g'(0).

已知 $f(0) > 0$ ， $g(0) < 0$ ，且 $f'(0) = g'(0) = 0$ 。根据题意可判断：

f''(0) < 0, \quad g''(0) > 0.

6

设 $I = \int_{0}^{\frac{\pi}{4}} \ln(\sin x) \, dx$ ， $J = \int_{0}^{\frac{\pi}{4}} \ln(\cot x) \, dx$ ， $K = \int_{0}^{\frac{\pi}{4}} \ln(\cos x) \, dx$ ，则 $I$ ， $J$ ， $K$ 的大小关系为（）

高等数学一元函数积分学定积分的计算

正确答案：B

在区间 $[0, \frac{\pi}{4}]$ 上，有 $\ln \sin x < \ln \cos x < \ln \cot x$ 。

根据定积分比较大小的性质，可知应选 (B)。

7

设 $A$ 为 3 阶矩阵，将 $A$ 的第 2 列加到第 1 列得矩阵 $B$ ，再交换 $B$ 的第 2 行与第 3 行得单位矩阵。

记 $P_1 = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ ， $P_2 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$ ，则 $A =$ （）

线性代数矩阵矩阵的运算与变换

正确答案：D

由初等变换及初等矩阵的性质易知 $P_{2} A P_{1} = E$ ，从而

A = P_{2}^{-1} P_{1}^{-1} = P_{2} P_{1}^{-1},

答案应选 (D)。

8

设 $\boldsymbol{A} = (\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}, \boldsymbol{\alpha}_{4})$ 是 $4$ 阶矩阵， $\boldsymbol{A}^*$ 为 $\boldsymbol{A}$ 的伴随矩阵。若 $(1, 0, 1, 0)^{\mathrm{T}}$ 是方程组 $\boldsymbol{A}\boldsymbol{x} = \boldsymbol{0}$ 的一个基础解系，则 $\boldsymbol{A}^*\boldsymbol{x} = \boldsymbol{0}$ 的基础解系可为( )

线性代数矩阵伴随矩阵与可逆矩阵

正确答案：D

由 $(1,0,1,0)^{\top}$ 是方程 $A\boldsymbol{X}=\boldsymbol{0}$ 的一个基础解系，可知 $r(A)=3$ ，从而 $r(A^{*})=1$ ，且 $|A|=0$ 。

于是 $A^{*}A = |A|E = 0$ ，即 $\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3, \boldsymbol{a}_4$ 为 $A^{*}\boldsymbol{X}=\boldsymbol{0}$ 的解。

由 $\boldsymbol{a}_1 + \boldsymbol{a}_3 = \boldsymbol{0}$ ，可知 $\boldsymbol{a}_1, \boldsymbol{a}_3$ 线性相关。又由 $r(A)=3$ ，可知 $\boldsymbol{a}_2, \boldsymbol{a}_3, \boldsymbol{a}_4$ 线性无关。

同时 $r(A^{*})=1$ ，因此 $\boldsymbol{a}_2, \boldsymbol{a}_3, \boldsymbol{a}_4$ 为 $A^{*}\boldsymbol{X}=\boldsymbol{0}$ 的基础解系。

故应选 (D)。

填空题

9

（填空题） $\lim\limits_{x \to 0} \left( \frac{1 + 2^{x}}{2} \right)^{\frac{1}{x}} =$

高等数学函数、极限、连续函数极限的计算

【答案】 $\sqrt{2}$

【解析】
首先，我们考虑极限：

\lim_{x \to 0} \left( \frac{1 + 2^x}{2} \right)^{\frac{1}{x}}

为了简化计算，我们取自然对数并利用指数函数的连续性：

\lim_{x \to 0} \left( \frac{1 + 2^x}{2} \right)^{\frac{1}{x}} = e^{\lim_{x \to 0} \frac{1}{x} \ln \left( \frac{1 + 2^x}{2} \right)}

接下来，我们处理指数部分：

\lim_{x \to 0} \frac{1}{x} \ln \left( \frac{1 + 2^x}{2} \right)

注意到：

\frac{1 + 2^x}{2} = 1 + \frac{2^x - 1}{2}

因此，我们可以将极限改写为：

\lim_{x \to 0} \frac{1}{x} \ln \left( 1 + \frac{2^x - 1}{2} \right)

当 $x \to 0$ 时， $\frac{2^x - 1}{2}$ 是一个无穷小量，因此我们可以使用近似公式 $\ln(1 + y) \approx y$ 当 $y \to 0$ 时：

\ln \left( 1 + \frac{2^x - 1}{2} \right) \approx \frac{2^x - 1}{2}

于是：

\lim_{x \to 0} \frac{1}{x} \cdot \frac{2^x - 1}{2}

进一步化简：

\frac{1}{2} \lim_{x \to 0} \frac{2^x - 1}{x}

我们知道：

\lim_{x \to 0} \frac{2^x - 1}{x} = \ln 2

因此：

\frac{1}{2} \cdot \ln 2 = \ln \sqrt{2}

最后，代入指数函数：

e^{\ln \sqrt{2}} = \sqrt{2}

所以：

\lim_{x \to 0} \left( \frac{1 + 2^x}{2} \right)^{\frac{1}{x}} = \sqrt{2}

10

（填空题）微分方程 $y' + y = e^{-x} \cos x$ 满足条件 $y(0) = 0$ 的解为 $y =$

高等数学常微分方程一阶非齐次线性微分方程

【答案】 $y = e^{-x} \sin x$

【解析】 已知方程的解为：

y = e^{-\int 1 \, dx} \left( C + \int e^{-x} \cos x \, e^{\int 1 \, dx} \, dx \right) = e^{-x} ( C + \sin x )

代入初始条件 $y(0) = 0$ 得：

0 = e^{0} ( C + \sin 0 ) = 1 \cdot ( C + 0 ) = C

因此 $C = 0$ 。

最终解为：

y = e^{-x} \sin x

11

（填空题）曲线 $y = \int_{0}^{x} \tan t \, dt \quad (0 \leq x \leq \frac{\pi}{4})$ 的弧长 $s =$

高等数学一元函数积分学定积分的应用

【答案】 $\ln(\sqrt{2} + 1)$

【解析】
要计算积分

s = \int_{0}^{\frac{\pi}{4}} \sqrt{1 + \tan^{2}x} \, dx

首先，利用三角恒等式

1 + \tan^{2}x = \sec^{2}x

因此

\sqrt{1 + \tan^{2}x} = \sqrt{\sec^{2}x} = |\sec x|

在区间 $[0, \frac{\pi}{4}]$ 上， $\sec x > 0$ ，所以

|\sec x| = \sec x

于是积分变为

s = \int_{0}^{\frac{\pi}{4}} \sec x \, dx

已知

\int \sec x \, dx = \ln |\sec x + \tan x| + C

因此

s = \left[ \ln (\sec x + \tan x) \right]_{0}^{\frac{\pi}{4}}

代入上下限：
当 $x = \frac{\pi}{4}$ 时，

\sec\left(\frac{\pi}{4}\right) = \sqrt{2}, \quad \tan\left(\frac{\pi}{4}\right) = 1

所以

\ln\left( \sec\frac{\pi}{4} + \tan\frac{\pi}{4} \right) = \ln(\sqrt{2} + 1)

当 $x = 0$ 时，

\sec 0 = 1, \quad \tan 0 = 0

所以

\ln(\sec 0 + \tan 0) = \ln(1 + 0) = \ln 1 = 0

因此

s = \ln(\sqrt{2} + 1) - 0 = \ln(\sqrt{2} + 1)

最终结果为

s = \ln(\sqrt{2} + 1)

12

（填空题）设随机变量 $X$ 的概率密度为

f(x) = \begin{cases} \lambda e^{-\lambda x}, & x > 0 \\ 0, & x \leq 0 \end{cases} \quad (\lambda > 0),

则

\int_{-\infty}^{+\infty} x f(x) \, dx =

概率论与数理统计随机变量的数字特征数学期望与方差

【答案】 $\frac{1}{\lambda}$

【解析】 已知指数分布的概率密度函数为 $f(x) = \lambda e^{-\lambda x}$ ，其中 $x \geq 0$ ， $\lambda > 0$ 。

其数学期望为：

E[X] = \int_{0}^{+\infty} x \cdot \lambda e^{-\lambda x} \, dx

令 $u = x$ ， $dv = \lambda e^{-\lambda x} dx$ ，则 $du = dx$ ， $v = -e^{-\lambda x}$ 。

使用分部积分法：

E[X] = \left[ -x e^{-\lambda x} \right]_{0}^{+\infty} + \int_{0}^{+\infty} e^{-\lambda x} \, dx

第一项在 $x \to +\infty$ 时趋于 0，在 $x = 0$ 时也为 0，因此该项为 0。

于是：

E[X] = \int_{0}^{+\infty} e^{-\lambda x} \, dx = \left[ -\frac{1}{\lambda} e^{-\lambda x} \right]_{0}^{+\infty}

当 $x \to +\infty$ 时， $e^{-\lambda x} \to 0$ ；当 $x = 0$ 时， $e^{-\lambda x} = 1$ 。

因此：

E[X] = 0 - \left( -\frac{1}{\lambda} \right) = \frac{1}{\lambda}

所以指数分布的数学期望为 $\frac{1}{\lambda}$ 。

13

（填空题）设平面区域 $D$ 由直线 $y = x$ 、圆 $x^{2} + y^{2} = 2y$ 及 $y$ 轴所组成，则二重积分 $\iint_{D} x y \, d\sigma =$

高等数学多元函数积分学重积分的计算

【答案】 $\frac{9}{32}$

【解析】
计算二重积分 $\iint_{D} xy \, d\sigma$ ，其中区域 $D$ 由极坐标给出。

首先，将积分转换为极坐标形式：

\iint_{D} xy \, d\sigma = \int_{0}^{\frac{\pi}{3}} d\theta \int_{0}^{2\sin\theta} r^{3} \sin\theta \cos\theta \, dr

先对 $r$ 进行积分：

\int_{0}^{2\sin\theta} r^{3} \, dr = \left[ \frac{r^{4}}{4} \right]_{0}^{2\sin\theta} = \frac{(2\sin\theta)^{4}}{4} = 4 \sin^{4}\theta

代入原式：

\int_{0}^{\frac{\pi}{3}} 4 \sin^{4}\theta \cos\theta \sin\theta \, d\theta = \int_{0}^{\frac{\pi}{3}} 4 \sin^{5}\theta \cos\theta \, d\theta

令 $u = \sin\theta$ ，则 $du = \cos\theta \, d\theta$ ，积分上下限变为：

\theta = 0 \Rightarrow u = 0, \quad \theta = \frac{\pi}{3} \Rightarrow u = \frac{\sqrt{3}}{2}

代入得：

\int_{0}^{\frac{\sqrt{3}}{2}} 4u^{5} \, du = 4 \left[ \frac{u^{6}}{6} \right]_{0}^{\frac{\sqrt{3}}{2}} = \frac{4}{6} \left( \frac{\sqrt{3}}{2} \right)^{6} = \frac{2}{3} \cdot \frac{27}{64} = \frac{54}{192} = \frac{9}{32}

因此，积分结果为：

\iint_{D} xy \, d\sigma = \frac{9}{32}

原答案中给出的 $\frac{7}{12}$ 有误，正确结果应为 $\frac{9}{32}$ 。

14

（填空题）二次型 $f(x_{1}, x_{2}, x_{3}) = x_{1}^{2} + 3x_{2}^{2} + x_{3}^{2} + 2x_{1}x_{2} + 2x_{1}x_{3} + 2x_{2}x_{3}$ ，则 $f$ 的正惯性指数为 ______。

线性代数二次型

【答案】 2

【解析】 【详解1】二次型 $f(x_{1}, x_{2}, x_{3}) = x_{1}^{2} + 3x_{2}^{2} + x_{3}^{2} + 2x_{1}x_{2} + 2x_{1}x_{3} + 2x_{2}x_{3}$ 可通过配方法化为 $y_{1}^{2} + 4y_{2}^{2}$ ，因此正惯性指数为 2。

【详解2】本题也可通过求二次型矩阵的特征值，进一步得到正惯性指数为 2。

解答题

15

（本题满分 10 分）已知函数

F(x) = \frac{\int_{0}^{x} \ln(1 + t^{2}) \, dt}{x^{3a}},

设

\lim_{x \to +\infty} F(x) = \lim_{x \to 0^{+}} F(x) = 0,

试求 $a$ 的取值范围。

高等数学一元函数微分学微分中值定理

【答案】 $\frac{1}{3} < a < 1$

【解析】 解：由 $\lim_{x \to +\infty} F(x) = 0$ ，所以至少 $a > 0$ 。

由 $\lim_{x \to 0^{+}} F(x) = 0$ ，可得

\lim_{x \to 0^{+}} F(x) = \lim_{x \to 0^{+}} \frac{\int_{0}^{x} \ln(1 + t^{2}) \, dt}{x^{3a}} = \lim_{x \to 0^{+}} \frac{\ln(1 + x^{2})}{3a x^{3a - 1}} = \lim_{x \to 0^{+}} \frac{x^{2}}{3a x^{3a - 1}} = 0

因此 $2 > 3a - 1$ ，即 $a < 1$ 。

又由 $\lim_{x \to +\infty} F(x) = 0$ ，可得

\begin{align*} \lim_{x \to +\infty} F(x) &= \lim_{x \to +\infty} \frac{\int_{0}^{x} \ln(1 + t^{2}) \, dt}{x^{3a}} \\ &= \lim_{x \to +\infty} \frac{\ln(1 + x^{2})}{3a x^{3a - 1}} \\ &= \lim_{x \to +\infty} \frac{2x}{1 + x^{2}} \cdot \frac{1}{3a(3a - 1)x^{3a - 2}} \\ &= \lim_{x \to +\infty} \frac{2x^{3 - 3a}}{1 + x^{2}} \cdot \frac{1}{3a(3a - 1)} \\ &= 0 \end{align*}

即 $3 - 3a < 2$ ，所以 $a > \frac{1}{3}$ 。

综上， $\frac{1}{3} < a < 1$ 。

16

（本题满分 10 分）
设函数 $y = y(x)$ 由参数方程

\begin{cases} x = \frac{1}{3}t^3 + t + \frac{1}{3}, \\ y = \frac{1}{3}t^3 - t + \frac{1}{3} \end{cases}

确定，求 $y = y(x)$ 的极值和曲线 $y = y(x)$ 的凹凸区间及拐点。

高等数学一元函数微分学函数的单调性、极值与最值

【答案】

极小值点：当 $t = 1$ 时， $(x, y) = \left( \frac{5}{3}, -\frac{1}{3} \right)$
极大值点：当 $t = -1$ 时， $(x, y) = \left( -1, 1 \right)$
拐点：当 $t = 0$ 时， $(x, y) = \left( \frac{1}{3}, \frac{1}{3} \right)$
凸区间： $t < 0$
凹区间： $t > 0$

【解析】
解：

\frac{dy}{dx} = \frac{t^2 - 1}{t^2 + 1}, \quad \frac{d^2y}{dx^2} = \frac{4t}{(t^2 + 1)^3}

当 $t = 1$ 时， $x = \frac{5}{3}$ ， $y = -\frac{1}{3}$ ，是极小值。

当 $t = -1$ 时， $x = -1$ ， $y = 1$ ，是极大值。

当 $t = 0$ 时， $x = \frac{1}{3}$ ， $y = \frac{1}{3}$ ，是拐点。

当 $t < 0$ 时，是凸区间。

当 $t > 0$ 时，是凹区间。

17

（本题满分 10 分）
设函数 $z = f(xy, yg(x))$ ，其中函数 $f$ 具有二阶连续偏导数，函数 $g(x)$ 可导且在 $x = 1$ 处取得极值 $g(1) = 1$ ，求

\left. \frac{\partial^{2} z}{\partial x \partial y} \right|_{\substack{x = 1 \\ y = 1}}

高等数学多元函数微分学偏导数的概念与计算

【答案】

\left. \frac{\partial^{2} z}{\partial x \partial y} \right|_{\substack{x = 1 \\ y = 1}} = f_{1}'(1,1) + f_{11}''(1,1)

【解析】
【详解】

首先，我们计算一阶偏导数：

\frac{\partial z}{\partial x} = f_{1}' y + f_{2}' g'(x)

接着，计算二阶混合偏导数：

\frac{\partial^{2} z}{\partial x \partial y} = f_{1}' + x y f_{11}'' + x f_{21}'' g'(x)

已知 $g(x)$ 在 $x = 1$ 处取得极值，因此：

g'(1) = 0

代入 $x = 1$ ， $y = 1$ 及 $g'(1) = 0$ ，得到：

\left. \frac{\partial^{2} z}{\partial x \partial y} \right|_{\substack{x = 1 \\ y = 1}} = f_{1}'(1,1) + f_{11}''(1,1)

18

（本题满分 10 分）
设函数 $y(x)$ 具有二阶导数，且曲线 $l: y = y(x)$ 与直线 $y = x$ 相切于原点。记 $\alpha$ 为曲线 $l$ 在点 $(x, y)$ 处切线的倾角，若 $\frac{d\alpha}{dx} = \frac{dy}{dx}$ ，求 $y(x)$ 的表达式。

高等数学一元函数微分学微分中值定理

【答案】 $y(x) = \arcsin\left(\frac{\sqrt{2}}{2} e^x\right) - \frac{\pi}{4}$

【解析】 由题意知 $y(0) = 0$ ， $y'(0) = 1$ 。因为 $\alpha$ 为曲线 $l$ 在点 $(x, y)$ 处切线的倾角，所以 $\tan\alpha = \frac{dy}{dx}$ 。

两边同时对 $x$ 求导，得：

\sec^2\alpha \cdot \frac{d\alpha}{dx} = \frac{d^2y}{dx^2}.

由题知 $\frac{d\alpha}{dx} = \frac{dy}{dx}$ ，且 $\sec^2\alpha = 1 + \tan^2\alpha$ ，代入得：

\frac{d^2y}{dx^2} = \frac{dy}{dx} + \left(\frac{dy}{dx}\right)^3.

结合初值条件，得到微分方程组：

\begin{cases} \frac{d^2y}{dx^2} = \frac{dy}{dx} + \left(\frac{dy}{dx}\right)^3, \\ y(0) = 0, \\ y'(0) = 1. \end{cases}

此方程不显含 $x$ ，令 $y' = p$ ，则 $y'' = p \frac{dp}{dy}$ ，代入方程得：

p \frac{dp}{dy} = p + p^3.

若 $p \neq 0$ ，两边除以 $p$ 得：

\frac{dp}{dy} = 1 + p^2.

分离变量得：

\frac{dp}{1 + p^2} = dy.

积分得：

\arctan p = y + C_1.

即：

y' = \tan(y + C_1).

由 $y'(0) = 1$ ，代入得：

\tan(C_1) = 1 \quad \Rightarrow \quad C_1 = \frac{\pi}{4}.

因此：

y' = \tan\left(y + \frac{\pi}{4}\right).

此为可分离变量方程，改写为：

\frac{dy}{dx} = \tan\left(y + \frac{\pi}{4}\right).

分离变量得：

\cot\left(y + \frac{\pi}{4}\right) dy = dx.

积分得：

\ln\left|\sin\left(y + \frac{\pi}{4}\right)\right| = x + C_2.

即：

\sin\left(y + \frac{\pi}{4}\right) = Ce^x.

由 $y(0) = 0$ 得：

\sin\left(\frac{\pi}{4}\right) = C \quad \Rightarrow \quad C = \frac{\sqrt{2}}{2}.

因此：

\sin\left(y + \frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} e^x.

解得：

y(x) = \arcsin\left(\frac{\sqrt{2}}{2} e^x\right) - \frac{\pi}{4}.

19

（本题满分 10 分）

（Ⅰ）证明：对任意的正整数 $n$ ，都有

\frac{1}{n + 1} < \ln\left(1 + \frac{1}{n}\right) < \frac{1}{n}

成立；

（Ⅱ）设

a_n = 1 + \frac{1}{2} + \cdots + \frac{1}{n} - \ln n \quad (n = 1, 2, \cdots),

证明数列 $\{ a_n \}$ 收敛。

高等数学函数、极限、连续数列敛散性的判定

【答案】 见解析

【解析】 证明：

① 先证明当 $0 \leqslant x \leqslant 1$ 时，有

\frac{x}{x + 1} < \ln(1 + x) < x.

可以利用导数得到函数单调性，结论是明显的。令 $x = \frac{1}{n}$ ，就得到证明结论。

② 先证明数列 $\{\boldsymbol{a}_n\}$ 单调递减：

\boldsymbol{a}_{n + 1} - \boldsymbol{a}_n = \frac{1}{n + 1} - \ln(n + 1) + \ln n = \frac{1}{n + 1} - \ln\left(1 + \frac{1}{n}\right) < 0.

再证明数列 $\{\boldsymbol{a}_n\}$ 有下界：

\begin{align*} \boldsymbol{a}_n &= 1 + \frac{1}{2} + \cdots + \frac{1}{n} - \ln n \\ &> \ln\left(1 + \frac{1}{1}\right) + \ln\left(1 + \frac{1}{2}\right) + \cdots + \ln\left(1 + \frac{1}{n}\right) - \ln n \\ &= \ln\left(\frac{2}{1} \cdot \frac{3}{2} \cdots \frac{n + 1}{n} \cdot \frac{1}{n}\right) \\ &= \ln\left(\frac{n + 1}{n}\right) > 0. \end{align*}

所以数列 $\{\boldsymbol{a}_n\}$ 收敛。

20

（本题满分 11 分）

一容器的内侧是由图中曲线绕 $y$ 轴旋转一周而成的曲面，该曲线由 $x^{2} + y^{2} = 2y \left(y \geqslant \frac{1}{2}\right)$ 与 $x^{2} + y^{2} = 1 \left(y \leqslant \frac{1}{2}\right)$ 连接而成。

（Ⅰ）求容器的容积；

（Ⅱ）若将容器内盛满的水从容器顶部全部抽出，至少需要做多少功？

（长度单位： $\mathrm{m}$ ，重力加速度为 $g \ \mathrm{m/s^{2}}$ ，水的密度为 $10^{3} \ \mathrm{kg/m^{3}}$ ）

高等数学一元函数积分学定积分的应用

【答案】
（Ⅰ） $\frac{9}{4} \pi$
（Ⅱ） $\frac{27}{4} \pi \times 10^3 g$

【解析】
(I) 容积 $V = V_1 + V_2 = 2V_1 = 2\pi \int_{\frac{1}{2}}^{1} \left(1 - y^2\right) dy = \frac{9}{4} \pi$ 。

(II) 功 $W = \int_{1}^{2} \rho g \cdot \pi x^2(y) \cdot (2 - y) dy$ 。

由于积分区间跨越上下两部分，需分段处理：

上半部分对应 $x^2(y) = 2y - y^2$ ，下半部分对应 $x^2(y) = 1 - y^2$ 。

因此：

W = \int_{\frac{1}{2}}^{2} 10^3 g \cdot \pi \left[ (2y - y^2) \text{} (1 - y^2) \text{} \right] \cdot (2 - y) dy

最终结果为：

W = \frac{27}{4} \pi \times 10^3 g

21

（本题满分 11 分）

已知函数 $f(x, y)$ 具有二阶连续偏导数，且 $f(1, y) = f(x, 1) = 0$ ， $\iint_{D} f(x, y) \, dx \, dy = a$ ，其中 $D = \{ (x, y) \mid 0 \leq x \leq 1, 0 \leq y \leq 1 \}$ ，计算二重积分 $I = \iint_{D} x y f_{xy}''(x, y) \, dx \, dy$ 。

高等数学多元函数积分学重积分的计算

【答案】 $I = a$

【解析】 根据二重积分的计算，有：

\iint\limits_D xyf_{xy}''(x,y) dxdy = \int_{0}^{1} x \left( \int_{0}^{1} y f_{xy}''(x,y) dy \right) dx

对内部积分进行计算：

\int_{0}^{1} y f_{xy}''(x,y) dy = \int_{0}^{1} y d f_{x}'(x,y) = \left[ y f_{x}'(x,y) \right]_{y=0}^{y=1} - \int_{0}^{1} f_{x}'(x,y) dy

= f_{x}'(x,1) - \int_{0}^{1} f_{x}'(x,y) dy = - \int_{0}^{1} f_{x}'(x,y) dy

代入原式：

= \int_{0}^{1} x \left( - \int_{0}^{1} f_{x}'(x,y) dy \right) dx = - \int_{0}^{1} \left( \int_{0}^{1} x f_{x}'(x,y) dx \right) dy

进一步计算：

- \int_{0}^{1} \left( \int_{0}^{1} x f_{x}'(x,y) dx \right) dy = - \int_{0}^{1} \left( \int_{0}^{1} x d f(x,y) \right) dy

= - \int_{0}^{1} \left( \left[ x f(x,y) \right]_{x=0}^{x=1} - \int_{0}^{1} f(x,y) dx \right) dy

= - \int_{0}^{1} \left( f(1,y) - \int_{0}^{1} f(x,y) dx \right) dy

= \iint\limits_D f(x,y) dxdy = a

22

（本题满分 11 分）

设向量组 $\boldsymbol{\alpha}_{1} = (1, 0, 1)^{\mathrm{T}}$ ， $\boldsymbol{\alpha}_{2} = (0, 1, 1)^{\mathrm{T}}$ ， $\boldsymbol{\alpha}_{3} = (1, 3, 5)^{\mathrm{T}}$ 不能由向量组 $\boldsymbol{\beta}_{1} = (1, 1, 1)^{\mathrm{T}}$ ， $\boldsymbol{\beta}_{2} = (1, 2, 3)^{\mathrm{T}}$ ， $\boldsymbol{\beta}_{3} = (3, 4, a)^{\mathrm{T}}$ 线性表示。

（Ⅰ）求 $a$ 的值；

（Ⅱ）将 $\boldsymbol{\beta}_{1}$ ， $\boldsymbol{\beta}_{2}$ ， $\boldsymbol{\beta}_{3}$ 用 $\boldsymbol{\alpha}_{1}$ ， $\boldsymbol{\alpha}_{2}$ ， $\boldsymbol{\alpha}_{3}$ 线性表示。

线性代数向量向量组之间的线性表示

【答案】
（Ⅰ） $a = 5$ 。
（Ⅱ） $\begin{pmatrix} \boldsymbol{\beta}_{1} & \boldsymbol{\beta}_{2} & \boldsymbol{\beta}_{3} \end{pmatrix} = \begin{pmatrix} \boldsymbol{\alpha}_{1} & \boldsymbol{\alpha}_{2} & \boldsymbol{\alpha}_{3} \end{pmatrix} \begin{pmatrix} 2 & 1 & 5 \\ 4 & 2 & 10 \\ -1 & 0 & -2 \end{pmatrix}$ 。

【解析】
(1) 易知 $\boldsymbol{\alpha}_{1}$ ， $\boldsymbol{\alpha}_{2}$ ， $\boldsymbol{\alpha}_{3}$ 线性无关。由于它们不能被 $\boldsymbol{\beta}_{1}$ ， $\boldsymbol{\beta}_{2}$ ， $\boldsymbol{\beta}_{3}$ 线性表出，可得 $\boldsymbol{\beta}_{1}$ ， $\boldsymbol{\beta}_{2}$ ， $\boldsymbol{\beta}_{3}$ 线性相关，从而 $r(\boldsymbol{\beta}_{1},\boldsymbol{\beta}_{2},\boldsymbol{\beta}_{3}) < 3$ 。

由

\begin{pmatrix} 1 & 1 & 3 \\ 1 & 2 & 4 \\ 1 & 3 & a \end{pmatrix} \to \begin{pmatrix} 1 & 1 & 3 \\ 0 & 1 & 1 \\ 0 & 2 & a - 3 \end{pmatrix} \to \begin{pmatrix} 1 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & a - 5 \end{pmatrix}

得 $a = 5$ 。

(2) 由

\begin{pmatrix} 1 & 0 & 1 & 1 & 1 & 3 \\ 0 & 1 & 3 & 1 & 2 & 4 \\ 1 & 1 & 5 & 1 & 3 & 5 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 1 & 1 & 1 & 3 \\ 0 & 1 & 3 & 1 & 2 & 4 \\ 0 & 1 & 4 & 0 & 2 & 2 \end{pmatrix}

\to \begin{pmatrix} 1 & 0 & 1 & 1 & 1 & 3 \\ 0 & 1 & 3 & 1 & 2 & 4 \\ 0 & 0 & 1 & -1 & 0 & -2 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 0 & 2 & 1 & 5 \\ 0 & 1 & 0 & 4 & 2 & 10 \\ 0 & 0 & 1 & -1 & 0 & -2 \end{pmatrix}

得

\begin{pmatrix} \boldsymbol{\beta}_{1} & \boldsymbol{\beta}_{2} & \boldsymbol{\beta}_{3} \end{pmatrix} = \begin{pmatrix} \boldsymbol{\alpha}_{1} & \boldsymbol{\alpha}_{2} & \boldsymbol{\alpha}_{3} \end{pmatrix} \begin{pmatrix} 2 & 1 & 5 \\ 4 & 2 & 10 \\ -1 & 0 & -2 \end{pmatrix}

23

（本题满分 11 分）

设 $A$ 为 3 阶实对称矩阵， $A$ 的秩为 2，且

A \begin{pmatrix} 1 & 1 \\ 0 & 0 \\ -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 1 \\ 0 & 0 \\ 1 & 1 \end{pmatrix}

（Ⅰ）求 $A$ 的所有特征值与特征向量；

（Ⅱ）求矩阵 $A$ 。

线性代数矩阵的特征值与特征向量

【答案】
（Ⅰ）特征值：-1, 1, 0；对应的特征向量分别为 $\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}$ , $\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$ , $\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$ 。
（Ⅱ）矩阵 $A = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}$ 。

【解析】
(1) 易知特征值 $-1$ 对应的特征向量为 $\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix},$
特征值 $1$ 对应的特征向量为 $\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}.$
由 $\mathrm{r}(A) = 2$ 知 $A$ 的另一个特征值为 $0$ 。
因为实对称矩阵不同特征值的特征向量正交，从而特征值 $0$ 对应的特征向量为 $\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}.$

(2) 由

A = \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix} \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix}^{-1}

得

A = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}.