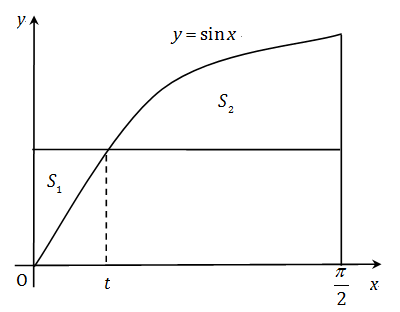卷 4 判断题 本题满分10分,每小题2分
1 lim x → 0 e x 1 = ∞
【答案】 不正确,该极限不存在。
【解析】 当
x → 0 + x 1 → + ∞ e x 1 → + ∞ x → 0 − x 1 → − ∞ e x 1 → 0 lim x → 0 e x 1
2 ∫ − π π x 4 sin x d x = 0
【答案】 正确
【解析】 考虑被积函数
f ( x ) = x 4 sin x f ( − x ) = ( − x ) 4 sin ( − x ) = x 4 ( − sin x ) = − x 4 sin x = − f ( x ) f ( x ) [ − π , π ] ∫ − π π x 4 sin x d x = 0
3 若级数
∑ n = 1 ∞ a n ∑ n = 1 ∞ b n ∑ n = 1 ∞ ( a n + b n )
【答案】 不正确
【解析】 a n = 1 b n = − 1 ∑ n = 1 ∞ a n = 1 + 1 + 1 + ⋯ ∑ n = 1 ∞ b n = − 1 − 1 − 1 − ⋯ ∑ n = 1 ∞ ( a n + b n ) = ∑ n = 1 ∞ ( 1 − 1 ) = ∑ n = 1 ∞ 0 = 0
4 假设
D A r D = 0 D r + 1 0 A r + 1 0
【答案】 正确。
【解析】 A r D = 0 D r + 1 0 D R C ∣ R ∣ = r ∣ C ∣ = r D = 0 R C
对于任意不在
R i C j A [ R ∪ { i } , C ∪ { j }] 0
[ D A i C A R j a ij ]
其中
A R j R j A i C i C a ij ( i , j ) D
det = det ( D ) ⋅ ( a ij − A i C D − 1 A R j ) = 0
因为
det ( D ) = 0 a ij = A i C D − 1 A R j w i = A i C D − 1 w i j j ∈ C i j a ij A i C A i C = w i D a ij = w i A R j j ∈ / C a ij = w i A R j j a ij = w i A R j i R
因此,所有行都可以由行集
R r D = 0 r r r + 1 0
5 连续型随机变量取任何给定实数值的概率都等于
0
【答案】 正确
【解析】 连续型随机变量的概率分布由概率密度函数描述,其概率计算基于积分。x P ( X = x ) x
选择题 本题满分10分,每小题2分
6 函数( )在其定义域内连续.
查看答案与解析
正确答案:A 【解析】 对于选项A,函数
f ( x ) = ln x + sin x x > 0 ( 0 , + ∞ ) ln x sin x f ( x )
对于选项B,函数在
x = 0 sin 0 = 0 cos 0 = 1 f ( 0 ) = sin 0 = 0
对于选项C,函数在
x = 0 0 + 1 = 1 0 − 1 = − 1 f ( 0 ) = 0
对于选项D,函数在
x = 0 f ( 0 ) = 0 x → 0 f ( x ) = ∣ x ∣ 1 → + ∞
因此,只有选项A在其定义域内连续。
7 若函数
f ( x ) ( a , b ) x 1 x 2 ( a , b ) x 1 < x 2 ξ
查看答案与解析
正确答案:C 【解析】 f ( x ) [ x 1 , x 2 ] ( x 1 , x 2 ) ξ ∈ ( x 1 , x 2 )
f ( x 2 ) − f ( x 1 ) = f ′ ( ξ ) ( x 2 − x 1 )
本题中,函数
f ( x ) ( a , b ) x 1 x 2 ( a , b ) x 1 < x 2 [ x 1 , x 2 ] ⊂ ( a , b ) C 正确。
选项 A、B、D 均涉及区间端点
a b
8 广义积分( )收敛.
查看答案与解析
正确答案:C 【解析】 u = ln x ∫ 1 + ∞ u d u
对于选项B,令
u = ln x ∫ 1 + ∞ u 1 d u
对于选项C,令
u = ln x ∫ 1 + ∞ u 2 1 d u 1
对于选项D,令
u = ln x ∫ 1 + ∞ u 1 d u
因此,只有选项C收敛。
9 假设
A n r < n A n
查看答案与解析
正确答案:A 【解析】 r r
选项 B 错误,因为虽然存在
r r r
选项 C 错误,因为任意
r
选项 D 错误,因为当
r > n /2 r r r
10 若二事件
A B P ( A B ) = 0
查看答案与解析
正确答案:C 【解析】 A B P ( A B ) = 0 A B 0 A B 0 0 A B C
选项
A P ( A B ) = 0 A B A B 选项
B P ( A B ) = 0 A B 选项
D P ( A B ) = 0 P ( A ) = 0 P ( B ) = 0 P ( A ) P ( B ) 0 P ( A B ) 0 计算题 本题满分16分,每小题4分
11 求极限
lim x → 0 ( 1 + x e x ) x 1
【答案】 e
【解析】 L = lim x → 0 ( 1 + x e x ) x 1
对表达式取自然对数:
ln L = x → 0 lim x ln ( 1 + x e x )
此为
0 0
ln L = x → 0 lim d x d x d x d ln ( 1 + x e x ) = x → 0 lim 1 1 + x e x 1 ⋅ ( e x + x e x ) = x → 0 lim 1 + x e x e x ( 1 + x )
代入
x = 0
1 + 0 e 0 ( 1 + 0 ) = 1
故
ln L = 1 L = e
因此,所求极限为:
e
12 y = ln 1 + x 2 + 1 1 + x 2 − 1 y ′
【答案】
【解析】
设
u = 1 + x 2 + 1 1 + x 2 − 1 y = ln u y ′ = u u ′ u ′ v = 1 + x 2 u = v + 1 v − 1 v ′ = 1 + x 2 x
u ′ = ( v + 1 ) 2 ( v ′ ) ( v + 1 ) − ( v − 1 ) ( v ′ ) = ( v + 1 ) 2 v ′ [( v + 1 ) − ( v − 1 )] = ( v + 1 ) 2 v ′ ⋅ 2 = ( v + 1 ) 2 2 v ′
代入
v ′ v
u ′ = ( 1 + x 2 + 1 ) 2 2 ⋅ 1 + x 2 x = 1 + x 2 ( 1 + x 2 + 1 ) 2 2 x 现在,
y ′ = u u ′ = 1 + x 2 + 1 1 + x 2 − 1 1 + x 2 ( 1 + x 2 + 1 ) 2 2 x = 1 + x 2 ( 1 + x 2 + 1 ) 2 2 x ⋅ 1 + x 2 − 1 1 + x 2 + 1 = 1 + x 2 ( 1 + x 2 + 1 ) ( 1 + x 2 − 1 ) 2 x ( 1 + x 2 + 1 ) ( 1 + x 2 − 1 ) = ( 1 + x 2 ) − 1 = x 2
因此,导数为
x 1 + x 2 2
13 z = arctan x − y x + y d z
【答案】
d z = x 2 + y 2 x d y − y d x
【解析】
给定
z = arctan x − y x + y d z u = x − y x + y z = arctan u d z = ∂ x ∂ z d x + ∂ y ∂ z d y ∂ x ∂ z ∂ y ∂ z
∂ x ∂ z = 1 + u 2 1 ⋅ ∂ x ∂ u , ∂ y ∂ z = 1 + u 2 1 ⋅ ∂ y ∂ u .
计算
∂ x ∂ u ∂ y ∂ u
∂ x ∂ u = ( x − y ) 2 ( x − y ) ⋅ 1 − ( x + y ) ⋅ 1 = ( x − y ) 2 − 2 y ,
∂ y ∂ u = ( x − y ) 2 ( x − y ) ⋅ 1 − ( x + y ) ⋅ ( − 1 ) = ( x − y ) 2 2 x .
计算
1 + u 2
u 2 1 + u 2 = ( x − y x + y ) 2 , = 1 + ( x − y ) 2 ( x + y ) 2 = ( x − y ) 2 ( x − y ) 2 + ( x + y ) 2 = ( x − y ) 2 2 x 2 + 2 y 2 = ( x − y ) 2 2 ( x 2 + y 2 ) .
所以,
1 + u 2 1 = 2 ( x 2 + y 2 ) ( x − y ) 2 .
代入偏导数:
∂ x ∂ z = 2 ( x 2 + y 2 ) ( x − y ) 2 ⋅ ( x − y ) 2 − 2 y = x 2 + y 2 − y ,
∂ y ∂ z = 2 ( x 2 + y 2 ) ( x − y ) 2 ⋅ ( x − y ) 2 2 x = x 2 + y 2 x .
因此,全微分为:
d z = ∂ x ∂ z d x + ∂ y ∂ z d y = x 2 + y 2 − y d x + x 2 + y 2 x d y = x 2 + y 2 x d y − y d x .
14 求不定积分
∫ e 2 x − 1 d x
【答案】
【解析】
令
u = 2 x − 1 u 2 = 2 x − 1 x = 2 u 2 + 1 d x = u d u
对
∫ u e u d u v = u d w = e u d u d v = d u w = e u
∫ v d w = v w − ∫ w d v
代入得:
∫ u e u d u = u e u − ∫ e u d u = u e u − e u + C = e u ( u − 1 ) + C
代回
u = 2 x − 1
∫ e 2 x − 1 d x = e 2 x − 1 ( 2 x − 1 − 1 ) + C 验证:对结果求导,可得原被积函数,故积分正确。
解答题 15 考虑函数
y = sin x 0 ≤ x ≤ 2 π
(1)
t S 1 S 2 S = S 1 + S 2
(2)
t S = S 1 + S 2
【答案】 t = 4 π t = 0
【解析】 y = sin x [ 0 , 2 π ] S = S 1 + S 2 S 1 x = 0 x = t y = sin t y = sin x S 1 = ∫ 0 t ( sin t − sin x ) d x S 2 x = t x = 2 π y = sin x y = sin t S 2 = ∫ t 2 π ( sin x − sin t ) d x S
S = ∫ 0 t ( sin t − sin x ) d x + ∫ t 2 π ( sin x − sin t ) d x
首先,计算
∫ 0 t ( sin t − sin x ) d x = t sin t + cos t − 1 ∫ t 2 π ( sin x − sin t ) d x = cos t − sin t ( 2 π − t )
S = t sin t + cos t − 1 + cos t − sin t ( 2 π − t ) = sin t ( 2 t − 2 π ) + 2 cos t − 1
求导
S ′ ( t )
S ′ ( t ) = d t d [ sin t ( 2 t − 2 π ) + 2 cos t − 1 ] = cos t ( 2 t − 2 π ) + sin t ⋅ 2 − 2 sin t = cos t ( 2 t − 2 π )
令
S ′ ( t ) = 0 cos t ( 2 t − 2 π ) = 0 [ 0 , 2 π ] cos t = 0 t = 2 π 2 t − 2 π = 0 t = 4 π
S ( 0 ) = sin 0 ( 2 ⋅ 0 − 2 π ) + 2 cos 0 − 1 = 0 + 2 − 1 = 1 S ( 4 π ) = sin 4 π ( 2 ⋅ 4 π − 2 π ) + 2 cos 4 π − 1 = 2 2 ⋅ 0 + 2 − 1 = 2 − 1 ≈ 0.414 S ( 2 π ) = sin 2 π ( 2 ⋅ 2 π − 2 π ) + 2 cos 2 π − 1 = 1 ⋅ 2 π + 0 − 1 = 2 π − 1 ≈ 0.570 S t = 4 π t = 0 t = 4 π t = 0 16 将函数
f ( x ) = x 2 − 3 x + 2 1 x
【答案】
函数
f ( x ) = x 2 − 3 x + 2 1 x
f ( x ) = n = 0 ∑ ∞ ( 1 − 2 n + 1 1 ) x n
收敛区间为
( − 1 , 1 )
【解析】
函数
f ( x ) = x 2 − 3 x + 2 1 ( x − 1 ) ( x − 2 )
f ( x ) = 1 − x 1 − 2 − x 1 .
已知几何级数展开
1 − x 1 = n = 0 ∑ ∞ x n , ∣ x ∣ < 1 ,
以及
2 − x 1 = 2 1 ⋅ 1 − 2 x 1 = n = 0 ∑ ∞ 2 n + 1 x n , ∣ x ∣ < 2.
两式相减得
f ( x ) = n = 0 ∑ ∞ x n − n = 0 ∑ ∞ 2 n + 1 x n = n = 0 ∑ ∞ ( 1 − 2 n + 1 1 ) x n .
该幂级数的收敛半径
R = 1 x = 0 x = 1 ∣ x ∣ = 1
( − 1 , 1 ) .
17 计算二重积分
I = ∬ D e x 2 d x d y D y = x y = x 3
【答案】
2 e − 1
【解析】
积分区域
D y = x y = x 3 x = 0 x = 1 x [ 0 , 1 ] x y y = x 3 y = x
I = ∫ 0 1 ∫ x 3 x e x 2 d y d x
先对
y e x 2 y
∫ x 3 x e x 2 d y = e x 2 [ y ] x 3 x = e x 2 ( x − x 3 )
因此,
I = ∫ 0 1 e x 2 ( x − x 3 ) d x = ∫ 0 1 e x 2 x ( 1 − x 2 ) d x
令
t = x 2 d t = 2 x d x x d x = 2 d t x = 0 t = 0 x = 1 t = 1
I = ∫ 0 1 e t ( 1 − t ) ⋅ 2 d t = 2 1 ∫ 0 1 e t ( 1 − t ) d t
计算积分
∫ 0 1 e t ( 1 − t ) d t
∫ 0 1 e t ( 1 − t ) d t = ∫ 0 1 e t d t − ∫ 0 1 t e t d t
其中,
∫ 0 1 e t d t = [ e t ] 0 1 = e − 1
对于
∫ 0 1 t e t d t u = t d v = e t d t d u = d t v = e t
∫ t e t d t = t e t − ∫ e t d t = t e t − e t + C
所以,
∫ 0 1 t e t d t = [ t e t − e t ] 0 1 = ( 1 ⋅ e − e ) − ( 0 ⋅ e 0 − e 0 ) = ( e − e ) − ( 0 − 1 ) = 1
因此,
∫ 0 1 e t ( 1 − t ) d t = ( e − 1 ) − 1 = e − 2
代入原式:
I = 2 1 ( e − 2 ) = 2 e − 1
故二重积分的值为
2 e − 1
18 已知某商品的需求量
x p η = − 3 p 3 1
【答案】 x = e − p 3
【解析】 η = x p d p d x = − 3 p 3
x 1 d p d x = − 3 p 2
两边积分得
∫ x 1 d x = ∫ − 3 p 2 d p
即
ln ∣ x ∣ = − p 3 + C
其中
C
取指数得
x = e C e − p 3
由市场最大需求量为 1(万件),即当
p = 0 x = 1
1 = e C ⋅ e 0
所以
e C = 1
因此需求函数为
x = e − p 3
验证弹性:
d p d x = − 3 p 2 e − p 3
则
η = x p d p d x = e − p 3 p ⋅ ( − 3 p 2 e − p 3 ) = − 3 p 3
符合给定条件。
19 解线性方程组
⎩ ⎨ ⎧ 2 x 1 − x 2 + 4 x 3 − 3 x 4 = − 4 , x 1 + x 3 − x 4 = − 3 , 3 x 1 + x 2 + x 3 = 1 , 7 x 1 + 7 x 3 − 3 x 4 = 3.
【答案】
x 1 = 3 − t , x 2 = − 8 + 2 t , x 3 = t , x 4 = 6 t
【解析】
写出方程组的增广矩阵:
2 1 3 7 − 1 0 1 0 4 1 1 7 − 3 − 1 0 − 3 − 4 − 3 1 3 首先,将第二行与第一行交换,以便第一行第一个元素为1:
1 2 3 7 0 − 1 1 0 1 4 1 7 − 1 − 3 0 − 3 − 3 − 4 1 3 用第二行减去2倍第一行:
R 2 − 2 R 1 ( 0 , − 1 , 2 , − 1 , 2 ) R 3 − 3 R 1 ( 0 , 1 , − 2 , 3 , 10 ) R 4 − 7 R 1 ( 0 , 0 , 0 , 4 , 24 )
1 0 0 0 0 − 1 1 0 1 2 − 2 0 − 1 − 1 3 4 − 3 2 10 24 将第二行乘以-1:
R 2 × ( − 1 ) ( 0 , 1 , − 2 , 1 , − 2 )
1 0 0 0 0 1 1 0 1 − 2 − 2 0 − 1 1 3 4 − 3 − 2 10 24 用第三行减去第二行:
R 3 − R 2 ( 0 , 0 , 0 , 2 , 12 )
1 0 0 0 0 1 0 0 1 − 2 0 0 − 1 1 2 4 − 3 − 2 12 24 将第三行除以2:
R 3 ÷ 2 ( 0 , 0 , 0 , 1 , 6 ) R 4 ÷ 4 ( 0 , 0 , 0 , 1 , 6 )
1 0 0 0 0 1 0 0 1 − 2 0 0 − 1 1 1 1 − 3 − 2 6 6 第四行与第三行相同,因此第四行是冗余的,可忽略。从第三行得
x 4 = 6 x 2 − 2 x 3 + x 4 = − 2 x 4 = 6 x 2 − 2 x 3 = − 8 x 1 + x 3 − x 4 = − 3 x 4 = 6 x 1 + x 3 = 3 x 3 = t t x 1 = 3 − t x 2 = − 8 + 2 t x 4 = 6
20 假设矩阵
A B A B = A + 2 B A = 4 1 − 1 2 1 2 3 0 3 B
【答案】
【解析】
给定关系式
A B = A + 2 B
将方程整理为
A B − 2 B = A
( A − 2 I ) B = A ,
其中
I A − 2 I
A − 2 I = 4 1 − 1 2 1 2 3 0 3 − 2 0 0 0 2 0 0 0 2 = 2 1 − 1 2 − 1 2 3 0 1 然后求逆矩阵
( A − 2 I ) − 1
2 1 − 1 2 − 1 2 3 0 1 1 0 0 0 1 0 0 0 1 行约简后得到:
( A − 2 I ) − 1 = 1 1 − 1 − 4 − 5 6 − 3 − 3 4 然后计算
B = ( A − 2 I ) − 1 A
B = 1 1 − 1 − 4 − 5 6 − 3 − 3 4 4 1 − 1 2 1 2 3 0 3 = 3 2 − 2 − 8 − 9 12 − 6 − 6 9 验证:计算
A B A + 2 B
21 求矩阵
A = − 3 0 − 1 − 1 − 1 0 2 4 1
【答案】 λ = 1 0 2 1
【解析】 A − λ I = − 3 − λ 0 − 1 − 1 − 1 − λ 0 2 4 1 − λ
det ( A − λ I ) = ( − 3 − λ ) det ( − 1 − λ 0 4 1 − λ ) − ( − 1 ) det ( 0 − 1 4 1 − λ ) + 2 det ( 0 − 1 − 1 − λ 0 ) = ( − 3 − λ ) [( − 1 − λ ) ( 1 − λ )] + 1 ⋅ [ 0 ⋅ ( 1 − λ ) − 4 ⋅ ( − 1 )] + 2 ⋅ [ 0 ⋅ 0 − ( − 1 − λ ) ⋅ ( − 1 )] = ( − 3 − λ ) ( λ 2 − 1 ) + 4 + 2 ( − 1 − λ ) = ( − 3 − λ ) ( λ 2 − 1 ) + 4 − 2 − 2 λ = ( − 3 − λ ) ( λ 2 − 1 ) + 2 − 2 λ
展开得:
= − 3 λ 2 + 3 − λ 3 + λ + 2 − 2 λ
= − λ 3 − 3 λ 2 − λ + 5
特征方程为
− λ 3 − 3 λ 2 − λ + 5 = 0 λ 3 + 3 λ 2 + λ − 5 = 0 λ = 1 ( λ − 1 ) ( λ 2 + 4 λ + 5 ) = 0 λ 2 + 4 λ + 5 = 0 4 2 − 4 ⋅ 1 ⋅ 5 = − 4 < 0 λ = 1 ( A − I ) v = 0
− 4 0 − 1 − 1 − 2 0 2 4 0 x y z = 0 0 0 由第三行
− x = 0 x = 0 − 2 y + 4 z = 0 y = 2 z − 4 ⋅ 0 − y + 2 z = − y + 2 z = 0 z = t y = 2 t 0 2 t t = t 0 2 1 t = 0
计算题 22 已知随机变量
X
P { X = 1 } = 0.2 , P { X = 2 } = 0.3 , P { X = 3 } = 0.5 ,
试写出其分布函数
F ( x )
【答案】
F ( x ) = ⎩ ⎨ ⎧ 0 0.2 0.5 1 x < 1 1 ≤ x < 2 2 ≤ x < 3 x ≥ 3 【解析】 X F ( x ) F ( x ) = P { X ≤ x } X F ( x )
当
x < 1 X ≤ x F ( x ) = 0 当
1 ≤ x < 2 X ≤ x X = 1 F ( x ) = P { X = 1 } = 0.2 当
2 ≤ x < 3 X ≤ x X = 1 X = 2 F ( x ) = P { X = 1 } + P { X = 2 } = 0.2 + 0.3 = 0.5 当
x ≥ 3 X ≤ x F ( x ) = 1 综上,得到分布函数如上所示。
23 已知随机变量
Y f ( y ) = { a 2 y e − a 2 u 2 , 0 , y > 0 , y ≤ 0 , Z = Y 1 EZ
【答案】
【解析】
已知随机变量
Y f ( y ) = a 2 y e − a 2 y 2 y > 0 Z = Y 1 EZ
EZ = E [ Y 1 ] = ∫ 0 ∞ y 1 f ( y ) d y = ∫ 0 ∞ y 1 ⋅ a 2 y e − a 2 y 2 d y = a 2 1 ∫ 0 ∞ e − a 2 y 2 d y .
计算积分
∫ 0 ∞ e − a 2 y 2 d y u = a y d y = a d u u = 0 u = ∞
∫ 0 ∞ e − a 2 y 2 d y = ∫ 0 ∞ e − u 2 ⋅ a d u = a ∫ 0 ∞ e − u 2 d u .
已知
∫ 0 ∞ e − u 2 d u = 2 π
因此,
故随机变量
Z 2 a π
24 假设有两箱同种零件:第一箱内装
50 10 30 18
(1) 先取出的零件是一等品的概率
p
(2) 在先取出的是一等品的条件下,第二次取出的零件仍然是一等品的条件概率
q
【答案】 p = 5 2 q = 1421 690
【解析】 A H 1 H 2 P ( H 1 ) = P ( H 2 ) = 2 1 H 1 P ( A ∣ H 1 ) = 50 10 = 5 1 H 2 P ( A ∣ H 2 ) = 30 18 = 5 3
P ( A ) = P ( A ∣ H 1 ) P ( H 1 ) + P ( A ∣ H 2 ) P ( H 2 ) = 5 1 × 2 1 + 5 3 × 2 1 = 5 4 × 2 1 = 5 2 .
故
p = 5 2
(2) 设事件
B q = P ( B ∣ A )
P ( B ∣ A ) = P ( A ) P ( A ∩ B ) .
首先求
P ( A ∩ B )
P ( A ∩ B ) = P ( A ∩ B ∣ H 1 ) P ( H 1 ) + P ( A ∩ B ∣ H 2 ) P ( H 2 ) .
给定
H 1
P ( A ∩ B ∣ H 1 ) = 50 10 × 49 9 = 245 9 .
给定
H 2
P ( A ∩ B ∣ H 2 ) = 30 18 × 29 17 = 145 51 .
所以:
P ( A ∩ B ) = 245 9 × 2 1 + 145 51 × 2 1 = 2 1 ( 245 9 + 145 51 ) .
计算括号内:
245 9 + 145 51 = 245 × 29 9 × 29 + 145 × 49 51 × 49 = 7105 261 + 7105 2499 = 7105 2760 = 1421 552 .
于是:
P ( A ∩ B ) = 2 1 × 1421 552 = 1421 276 .
代入条件概率公式:
q = P ( B ∣ A ) = 5 2 1421 276 = 1421 276 × 2 5 = 2842 1380 = 1421 690 .
故
q = 1421 690