卷 5
判断题
本题满分10分,每小题2分
1
同试卷 4 第 1 题
2
同试卷 4 第 2 题
3
若函数
f(x)
在区间
(a,b)
内严格单调增加,
则对于区间
(a,b)
内的任何一点
x
有
f′(x)>0
.
【答案】
错误
【解析】
函数在区间内严格单调增加,仅表明对于任意两点
x1<x2
,有
f(x1)<f(x2)
,但这并不保证函数在每一点处都可导,或者导数均大于零。例如,函数
f(x)=x3
在区间
(−1,1)
内严格单调增加,但在点
x=0
处,其导数
f′(0)=0
,而不满足
f′(x)>0
。因此,原说法错误。
4
若
A
为
n
阶方阵,
k
为常数,
则
∣kA∣=k∣A∣
.
【答案】 错误
对于
n
阶方阵
A
,行列式
∣kA∣
的计算公式为
∣kA∣=kn∣A∣,
而不是
k∣A∣
。
这是因为当矩阵
A
的每个元素都乘以常数
k
时,行列式作为多重线性函数,会因每一行都乘以
k
而整体乘以
k
的
n
次方。
例如,当
n=2
时,取
A
为单位矩阵
I
,则
∣kI∣=k2,
而
k∣I∣=k
,两者不相等,除非
n=1
。
因此,原命题不正确。
5
同试卷 4 第 5 题
选择题
本题满分10分,每小题2分
6
函数( )在其定义域内连续.
正确答案:A【解析】
函数在其定义域内连续,需满足定义域内每一点都连续。
选项A:
f(x)=x1
,定义域为
x=0
,在定义域内
x1
是初等函数,因此连续。
选项B:在
x=0
处,左极限为
sin0=0
,右极限为
cos0=1
,左右极限不相等,故不连续。
选项C:在
x=0
处,左极限为
0+1=1
,右极限为
0−1=−1
,函数值为0,三者不相等,故不连续。
选项D:在
x=0
处,当
x→0
时,
∣x∣1→∞
,极限不存在,故不连续。
因此,只有选项A在其定义域内连续。
7
同试卷 4 第 7 题
8
同试卷 4 第 8 题
9
同试卷 4 第 9 题
10
对于任意二事件
A
和
B
,有
P(A−B)=
正确答案:C对于任意二事件
A
和
B
,事件
A−B
表示
A
发生但
B
不发生,即
A
与
B
的补集的交集,记为
A∩Bc
。
根据概率的加法公式,事件
A
的概率可以分解为
A
与
B
相交的部分和
A
与
B
不相交的部分,即
P(A)=P(A∩B)+P(A∩Bc)
因此,
P(A∩Bc)=P(A)−P(A∩B)
通常,
P(A∩B)
写作
P(AB)
,所以
P(A−B)=P(A)−P(AB)
选项 C 正确。
- 选项 A 仅在
A
和
B
互斥时成立,但题目要求对任意事件均成立;
- 选项 B 和 D 通过代数验证均不等于
P(A−B)
。
计算题
本题满分20分,每小题4分
11
求极限
x→+∞limarctanxln(1+x1)
【答案】
0
【解析】
当
x→+∞
时,分子
ln(1+x1)→ln1=0
,分母
arctanx→2π=0
,因此极限为
0
。
12
同试卷 4 第 12 题
13
同试卷 4 第 13 题
14
计算定积分
【答案】
1
【解析】
考虑定积分
∫211e2x−1dx
。令
t=2x−1
,则
t2=2x−1
,即
x=2t2+1
,微分得
dx=tdt
。积分限变化:当
x=21
时,
t=0
;当
x=1
时,
t=1
。代入后积分变为
∫01tetdt
。
使用分部积分法计算
∫tetdt
,令
u=t
,
dv=etdt
,则
du=dt
,
v=et
。有:
∫tetdt=tet−∫etdt=tet−et+C=et(t−1)+C
代入定积分上下限:
[et(t−1)]01=(e1(1−1))−(e0(0−1))=(e⋅0)−(1⋅(−1))=0−(−1)=1
因此,积分结果为 1。
15
求不定积分
∫x4+2x2+5xdx
【答案】
41arctan(2x2+1)+C
【解析】
首先,分母
x4+2x2+5
可化为完全平方形式:
x4+2x2+5=(x2+1)2+4
。于是积分变为:
∫(x2+1)2+4xdx.
令
t=x2
,则
dt=2xdx
,即
xdx=2dt
。代入得:
∫(x2+1)2+4xdx=21∫(t+1)2+4dt.
再令
u=t+1
,则
du=dt
,积分变为:
21∫u2+4du=21⋅21arctan(2u)+C=41arctan(2u)+C.
回代
u=t+1
和
t=x2
,得:
41arctan(2x2+1)+C.
解答题
16
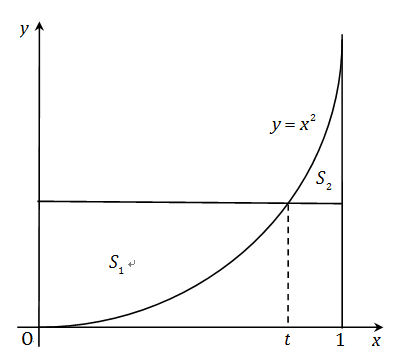
考虑函数
y=x2
,
0≤x≤1
(如图),问:
(1)
t
取何值时,图中阴影部分的面积
S1
与
S2
之和
S=S1+S2
最小?
(2)
t
取何值时,面积之和
S=S1+S2
最大?
【答案】
(1)
t=21
(2)
t=0
【解析】
- 建立面积函数
S(t)
从图中可以看出,水平线在
x=t
处与曲线
y=x2
相交,因此该水平线的方程为
y=t2
。
面积
S1
:它是从
x=0
到
x=t
之间,由直线
y=t2
和曲线
y=x2
围成的面积。
S1=∫0t(t2−x2)dx=[t2x−31x3]0t=t3−31t3=32t3
面积
S2
:它是从
x=t
到
x=1
之间,由曲线
y=x2
和直线
y=t2
围成的面积。
S2=∫t1(x2−t2)dx=[31x3−t2x]t1=(31−t2)−(31t3−t3)=31−t2+32t3
总面积
S(t)
:
S(t)=S1+S2=32t3+31−t2+32t3=34t3−t2+31
其中定义域为
t∈[0,1]
。
- 求解最值
为了找到最大值和最小值,我们对
S(t)
求导:
S′(t)=4t2−2t=2t(2t−1)
令
S′(t)=0
,得到驻点:l
t=0
或
t=21
。
(1) 何时面积
S
最小?
我们需要比较驻点和端点的函数值:
- 当
t=0
时:
S(0)=31≈0.333
- 当
t=21
时:
S(21)=34(81)−41+31=61−41+31=122−3+4=123=41=0.25
- 当
t=1
时:
S(1)=34−1+31=32≈0.667
结论: 当
t=21
时,面积之和
S
最小,最小值为
41
。
(2) 何时面积
S
最大?
比较上述计算结果:
结论: 当
t=1
时,面积之和
S
最大,最大值为
32
。
总结:
17
同试卷 4 第 17 题
18
假设某产品的总成本函数为
C(x)=400+3x+21x2
,
而需求函数为
p=x100
,其中
x
为产量(假定等于需求量),
p
为价格.试求:
(1) 边际成本;
(2) 边际效益;
(3) 边际利润:
(4) 收益的价格弹性.
【答案】
(1) 边际成本:
3+x
(2) 边际效益:
x50
(3) 边际利润:
x50−3−x
(4) 收益的价格弹性:
−1
【解析】
(1) 边际成本是成本函数对产量
x
的导数。
成本函数为
C(x)=400+3x+21x2,
求导得
C′(x)=3+x,
因此边际成本为
3+x
。
(2) 边际效益即边际收益,是收益函数对产量
x
的导数。
收益函数
R(x)=p⋅x
,代入需求函数
得
求导得
因此边际收益为
x50
。
(3) 边际利润是利润函数对产量
x
的导数。
利润函数
π(x)=R(x)−C(x)=100x−(400+3x+21x2), 求导得
π′(x)=R′(x)−C′(x)=x50−(3+x), 因此边际利润为
x50−3−x
。
(4) 收益的价格弹性定义为
Ep=dpdR⋅Rp.
首先,从需求函数
解出
x=p210000.
收益函数
R=p⋅x=p⋅p210000=p10000.
求导得
dpdR=−p210000.
代入弹性公式:
Ep=(−p210000)⋅p10000p=(−p210000)⋅10000p2=−1,
因此收益的价格弹性为
−1
。
19
同试卷 4 第 19 题
20
同试卷 4 第 20 题
21
同试卷 4 第 21 题
22
已知离散型随机变量
X
的概率分布为:
P{X=1}=0.2,P{X=2}=0.3,P{X=3}=0.5.
(1) 写出
X
的分布函数
F(x)
;
(2) 求
X
的数学期望和方差.
【答案】
(1)
X
的分布函数为:
F(x)=⎩⎨⎧00.20.51.0 x<1 1≤x<2 2≤x<3 x≥3 (2)
X
的数学期望为
2.3
,方差为
0.61
。
【解析】
(1) 分布函数
F(x)=P{X≤x}
。由于
X
是离散型随机变量,取值于
{1,2,3}
,因此:
- 当
x<1
时,
P{X≤x}=0
;
- 当
1≤x<2
时,
P{X≤x}=P{X=1}=0.2
;
- 当
2≤x<3
时,
P{X≤x}=P{X=1}+P{X=2}=0.2+0.3=0.5
;
- 当
x≥3
时,
P{X≤x}=P{X=1}+P{X=2}+P{X=3}=0.2+0.3+0.5=1.0
。
故得分布函数如上。
(2) 数学期望
E[X]=∑x⋅P{X=x}=1×0.2+2×0.3+3×0.5=0.2+0.6+1.5=2.3
方差
Var(X)=E[X2]−(E[X])2
其中
E[X2]=∑x2⋅P{X=x}=12×0.2+22×0.3+32×0.5=1×0.2+4×0.3+9×0.5=0.2+1.2+4.5=5.9
故
Var(X)=5.9−(2.3)2=5.9−5.29=0.61
23
同试卷 4 第 24 题