卷 4 填空题 本题满分15分,每小题3分
1 曲线
y = x + sin 2 x ( 2 π , 1 + 2 π )
【答案】 y = x + 1
【解析】 y = x + sin 2 x
y ′ = 1 + 2 sin x cos x = 1 + sin 2 x .
在点
x = 2 π
m = y ′ ( 2 π ) = 1 + sin π = 1 + 0 = 1.
已知切点坐标为
( 2 π , 1 + 2 π )
y − ( 1 + 2 π ) = 1 ⋅ ( x − 2 π ) .
化简得
y − 1 − 2 π = x − 2 π ,
即
y = x + 1.
因此,切线方程为
y = x + 1
2 幂级数
∑ n = 0 ∞ n + 1 x n
【答案】 [ − 1 , 1 )
【解析】 ∑ n = 0 ∞ n + 1 x n
L = n → ∞ lim a n a n + 1 = n → ∞ lim n + 1 x n n + 2 x n + 1 = n → ∞ lim x ⋅ n + 2 n + 1 = ∣ x ∣ n → ∞ lim n + 2 n + 1 = ∣ x ∣ ⋅ 1 = ∣ x ∣. 当
L < 1 ∣ x ∣ < 1 L > 1 ∣ x ∣ > 1 ∣ x ∣ = 1 当
x = 1 ∑ n = 0 ∞ n + 1 1 = ∑ k = 1 ∞ k 1 p = 2 1 < 1 p 当
x = − 1 ∑ n = 0 ∞ n + 1 ( − 1 ) n b n = n + 1 1 b n > 0 b n lim n → ∞ b n = 0 因此,收敛域为
[ − 1 , 1 )
3 齐次线性方程组
⎩ ⎨ ⎧ λ x 1 + x 2 + x 3 = 0 , x 1 + λ x 2 + x 3 = 0 , x 1 + x 2 + x 3 = 0 λ
【答案】
【解析】
计算行列式:
det ( A ) = λ ⋅ ( λ ⋅ 1 − 1 ⋅ 1 ) − 1 ⋅ ( 1 ⋅ 1 − 1 ⋅ 1 ) + 1 ⋅ ( 1 ⋅ 1 − λ ⋅ 1 ) = λ ( λ − 1 ) − 1 ⋅ 0 + 1 ⋅ ( 1 − λ ) = λ 2 − λ + 1 − λ = λ 2 − 2 λ + 1 = ( λ − 1 ) 2
因此,
det ( A ) = ( λ − 1 ) 2 det ( A ) = 0 ( λ − 1 ) 2 = 0 λ = 1 λ = 1 x 1 + x 2 + x 3 = 0 λ λ = 1
4 设随机变量
X
F ( x ) = ⎩ ⎨ ⎧ 0 , A sin x , 1 , x < 0 , 0 ≤ x ≤ 2 π , x > 2 π , 则
A = ,
P { ∣ X ∣ < 6 π } =
【答案】 2 1
【解析】 x = 2 π F ( 2 π ) = A sin 2 π = A F ( 2 π ) = 1 A = 1 P { ∣ X ∣ < 6 π } X x < 0 F ( x ) = 0
P { ∣ X ∣ < 6 π } = P { 0 ≤ X < 6 π }
由于
X
P { 0 ≤ X < 6 π } = F ( 6 π ) − F ( 0 )
计算得
F ( 6 π ) = 1 ⋅ sin 6 π = 2 1 , F ( 0 ) = 1 ⋅ sin 0 = 0
因此
P { ∣ X ∣ < 6 π } = 2 1 − 0 = 2 1
5 设随机变量
X E ( X ) = μ D ( X ) = σ 2 P { ∣ X − μ ∣ ≥ 3 σ } ≤
【答案】
9 1
【解析】
根据切比雪夫不等式,对于任意实数
k > 0
P { ∣ X − μ ∣ ≥ kσ } ≤ k 2 1
本题中
k = 3
P { ∣ X − μ ∣ ≥ 3 σ } ≤ 3 2 1 = 9 1
选择题 本题满分15分,每小题3分
6 设
f ( x ) = 2 x + 3 x − 2 x → 0
查看答案与解析
正确答案:B 【解析】
L = x → 0 lim x f ( x ) = x → 0 lim x 2 x + 3 x − 2 .
当
x → 0 2 x ln 2 + 3 x ln 3
L = x → 0 lim ( 2 x ln 2 + 3 x ln 3 ) = ln 2 + ln 3 = ln 6.
由于
ln 6 = 0 ln 6 = 1 f ( x ) x
7 在下列等式中,正确的结果是
查看答案与解析
正确答案:C 【解析】 ∫ f ( x ) d x f ( x )
∫ f ( x ) d x = F ( x ) + C ,
其中
F ′ ( x ) = f ( x )
d x d ∫ f ( x ) d x = d x d [ F ( x ) + C ] = F ′ ( x ) = f ( x ) ,
故选项 C 正确。
选项 A 错误,因为
∫ f ′ ( x ) d x = f ( x ) + C ,
结果中应包含积分常数。
选项 B 错误,因为
∫ df ( x ) = ∫ f ′ ( x ) d x = f ( x ) + C ,
同样缺少常数项。
选项 D 错误,因为
d ∫ f ( x ) d x = f ( x ) d x ,
而不是
f ( x )
8 同试卷 1 第 10 题
9 设
A B n × n
查看答案与解析
正确答案:C 【解析】A B n
∣ A + B ∣ = ∣2 I ∣ = 2 n ,
而
∣ A ∣ + ∣ B ∣ = 2 ,
当
n > 1
对于选项 B,矩阵乘法不满足交换律。例如取
A = [ 1 0 0 0 ] , B = [ 0 0 1 0 ] ,
则
A B = [ 0 0 1 0 ] , B A = [ 0 0 0 0 ] ,
两者不相等。
对于选项 D,矩阵的逆不满足分配律。例如当
A B
( A + B ) − 1 = ( 2 I ) − 1 = 2 1 I ,
而
A − 1 + B − 1 = I + I = 2 I ,
两者不相等。
对于选项 C,由行列式的性质可知
∣ A B ∣ = ∣ A ∣ ⋅ ∣ B ∣ , ∣ B A ∣ = ∣ B ∣ ⋅ ∣ A ∣ ,
由于标量乘法可交换,因此
∣ A B ∣ = ∣ B A ∣
恒成立。
10 以
A A
查看答案与解析
正确答案:D 【解析】 A A A ¬ ( P ∧ Q ) = ¬ P ∨ ¬ Q P Q ¬ P ¬ Q A
选项 D 表述为“甲种产品滞销或乙种产品畅销”,与上述推导完全一致。A
A 仅表示“甲滞销且乙畅销”; B 仅表示“甲、乙均畅销”; C 仅表示“甲滞销”。A 计算题 本题满分15分,每小题5分
11 求极限
lim x → ∞ ( sin x 1 + cos x 1 ) x
【答案】 e
【解析】 y = x 1 x → ∞ y → 0 +
y → 0 + lim ( sin y + cos y ) 1/ y
设该极限为
L
ln L = y → 0 + lim y ln ( sin y + cos y )
当
y → 0 + sin y + cos y → 1 ln ( sin y + cos y ) → 0 0 0 f ( y ) = ln ( sin y + cos y )
f ′ ( y ) = sin y + cos y cos y − sin y
在
y = 0
f ′ ( 0 ) = sin 0 + cos 0 cos 0 − sin 0 = 0 + 1 1 − 0 = 1
因此,
ln L = y → 0 + lim y ln ( sin y + cos y ) = f ′ ( 0 ) = 1
所以
L = e 1 = e e
12 已知
z = f ( u , v ) , u = x + y , v = x y f ( u , v ) ∂ x ∂ y ∂ 2 z
【答案】
∂ x ∂ y ∂ 2 z = f uu + u f uv + f v + v f vv
【解析】
已知
z = f ( u , v ) u = x + y v = x y f ( u , v ) ∂ x ∂ z ∂ y ∂ z
∂ x ∂ z = ∂ u ∂ f ∂ x ∂ u + ∂ v ∂ f ∂ x ∂ v = f u ⋅ 1 + f v ⋅ y = f u + y f v
∂ y ∂ z = ∂ u ∂ f ∂ y ∂ u + ∂ v ∂ f ∂ y ∂ v = f u ⋅ 1 + f v ⋅ x = f u + x f v
接下来求混合偏导数
∂ x ∂ y ∂ 2 z = ∂ y ∂ ( ∂ x ∂ z )
∂ x ∂ y ∂ 2 z = ∂ y ∂ ( f u + y f v ) = ∂ y ∂ f u + ∂ y ∂ ( y f v )
计算
∂ y ∂ f u
∂ y ∂ f u = ∂ u ∂ f u ∂ y ∂ u + ∂ v ∂ f u ∂ y ∂ v = f uu ⋅ 1 + f uv ⋅ x = f uu + x f uv
计算
∂ y ∂ ( y f v )
∂ y ∂ ( y f v ) = ∂ y ∂ y f v + y ∂ y ∂ f v = f v + y ( ∂ u ∂ f v ∂ y ∂ u + ∂ v ∂ f v ∂ y ∂ v ) = f v + y ( f vu ⋅ 1 + f vv ⋅ x ) = f v + y f vu + x y f vv
由于
f f uv = f vu
∂ x ∂ y ∂ 2 z = ( f uu + x f uv ) + ( f v + y f uv + x y f vv ) = f uu + ( x + y ) f uv + f v + x y f vv
代入
u = x + y v = x y
∂ x ∂ y ∂ 2 z = f uu + u f uv + f v + v f vv
这就是所求的结果。
13 求微分方程
y ′′ + 5 y ′ + 6 y = 2 e − x
【答案】
y = C 1 e − 2 x + C 2 e − 3 x + e − x C 1 C 2
【解析】
该微分方程为二阶线性非齐次方程,其通解由齐次解和非齐次特解两部分组成。y ′′ + 5 y ′ + 6 y = 0 r 2 + 5 r + 6 = 0 r 1 = − 2 r 2 = − 3 y h = C 1 e − 2 x + C 2 e − 3 x 2 e − x e − x y p = A e − x
y p ′ = − A e − x , y p ′′ = A e − x ,
代入得
A e − x − 5 A e − x + 6 A e − x = 2 A e − x = 2 e − x ,
解得
A = 1 y p = e − x
y = C 1 e − 2 x + C 2 e − 3 x + e − x .
解答题 14 设某厂家打算生产一批商品投放市场.已知该商品的需求函数为
P = P ( x ) = 10 e − 2 x ,
且最大需求量为
6 x P
(1) 求该商品的收益函数和边际收益函数.
(2) 求使收益最大时的产量、最大收益和相应的价格.
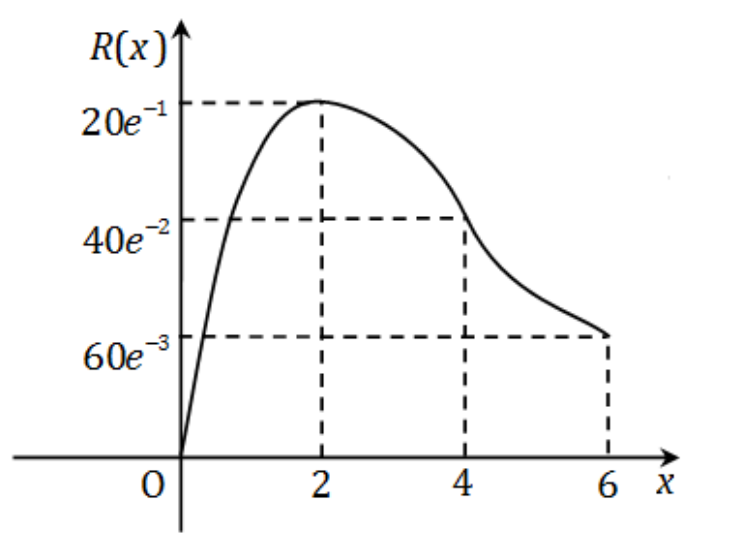
(3) 画出收益函数的图形.
【答案】 R ( x ) = 10 x e − 2 x MR ( x ) = e − 2 x ( 10 − 5 x ) x = 2 e 20 e 10 x ∈ [ 0 , 6 ] ( 0 , 0 ) x = 2 e 20 ( 6 , e 3 60 )
【解析】 R ( x ) MR
R ( x ) = x P = 10 x e − 2 x , MR = d x d R = 5 ( 2 − x ) e − 2 x , 0 ≤ x ≤ 6.
(II) 由
d x d R = 5 ( 2 − x ) e − 2 x = 0 x = 2
d x 2 d 2 R x = 2 = 2 5 ( x − 4 ) e − 2 x x = 2 = − e 5 < 0. 因此
R ( x ) x = 2 R ( 2 ) = e 20 e 20 e 10
(III) 由以上分析可列下表,并画出收益函数的图形。
x [0, 2) 2 (2, 4) 4 (4, 6) R ′ + 0 - - - R ′′ - - - 0 + R ↑, 凸 极大值
e 20 ↓, 凸 拐点
( 4 , e 2 40 ) ↓, 凹
15 已知函数
f ( x ) = { x , 2 − x , 0 ≤ x ≤ 1 , 1 ≤ x ≤ 2.
(1)
S 0 = ∫ 0 2 f ( x ) e − x d x
(2)
S 1 = ∫ 2 4 f ( x − 2 ) e − x d x
(3)
S n = ∫ 2 n 2 n + 2 f ( x − 2 n ) e − x d x ( n = 2 , 3 , ⋯ )
(4)
S = ∑ n = 0 ∞ S n
【答案】 S 0 = 1 − e 2 + e 2 1 S 1 = e 2 1 − e 3 2 + e 4 1 S n = S 0 e − 2 n = ( 1 − e 2 + e 2 1 ) e − 2 n S = e + 1 e − 1
【解析】
(Ⅰ)
f ( x )
S 0 = ∫ 0 2 f ( x ) e − x d x = ∫ 0 1 f ( x ) e − x d x + ∫ 1 2 f ( x ) e − x d x
= ∫ 0 1 x e − x d x + ∫ 1 2 ( 2 − x ) e − x d x = ( 1 − 2 e − 1 ) + e − 2 = ( 1 − e − 1 ) 2 .
(Ⅱ) 用定积分换元法,令
x − 2 = t
S 1 = ∫ 2 4 f ( x − 2 ) e − x d x = ∫ 0 2 f ( t ) e − ( t + 2 ) d t = e − 2 ∫ 0 2 f ( t ) e − t d t = S 0 e − 2 .
(Ⅲ) 用定积分换元法,令
x − 2 n = t
S n = ∫ 2 n 2 n + 2 f ( x − 2 n ) e − x d x = ∫ 0 2 f ( t ) e − ( t + 2 n ) d t = ∫ 0 2 f ( t ) e − t d t = S 0 e − 2 n .
(Ⅳ) 利用以上结果,有
S = n = 0 ∑ ∞ S n = n = 0 ∑ ∞ S 0 e − 2 n = S 0 n = 0 ∑ ∞ ( e − 2 ) n = 1 − e − 2 S 0 = e 2 − 1 e 2 S 0 = e + 1 e − 1 .
16 假设函数
f ( x ) [ a , b ] ( a , b ) f ′ ( x ) ≤ 0
F ( x ) = x − a 1 ∫ a x f ( t ) d t ,
证明在
( a , b ) F ′ ( x ) ≤ 0
【答案】 见解析
【解析】 F ( x ) = x − a 1 ∫ a x f ( t ) d t
F ′ ( x ) = − ∫ a x ( x − a ) 2 f ( t ) d t + x − a f ( x ) = ( x − a ) 2 ( x − a ) f ( x ) − ∫ a x f ( t ) d t .
方法一 :由积分中值定理,
∃ ξ ∈ ( a , x ) ∫ a x f ( t ) d t = f ( ξ ) ( x − a )
F ′ ( x ) = ( x − a ) 2 ( x − a ) f ( x ) − f ( ξ ) ( x − a ) = x − a f ( x ) − f ( ξ ) .
又因为
f ′ ( x ) ≤ 0 , a < ξ < x f ( x ) − f ( ξ ) ≤ 0 F ′ ( x ) ≤ 0
方法二 :令
g ( x ) = ( x − a ) f ( x ) − ∫ a x f ( t ) d t
g ′ ( x ) = f ( x ) + ( x − a ) f ′ ( x ) − f ( x ) = ( x − a ) f ′ ( x ) .
因为
x > a , f ′ ( x ) ≤ 0 g ′ ( x ) ≤ 0 g ( x ) ( a , b ) g ( x ) ≤ g ( a ) = 0 F ′ ( x ) = ( x − a ) 2 g ( x ) ≤ 0
17 已知
X = A X + B A = 0 − 1 − 1 1 1 0 0 1 − 1 B = 1 2 5 − 1 0 − 3 X
【答案】
【解析】 X = A X + B ( E − A ) X = B
( E − A ) − 1 = 1 1 1 − 1 0 0 0 − 1 2 − 1 = 3 1 0 − 3 0 2 2 − 1 1 1 1 , 所以
X = ( E − A ) − 1 B = 3 1 0 − 3 0 2 2 − 1 1 1 1 1 2 5 − 1 0 − 3 = 3 2 1 − 1 0 − 1 . 方法二:由
( E − A ) X = B ( E − A : B ) → ( E : X )
( E − A : B ) = 1 1 1 − 1 0 0 0 − 1 2 : : : 1 2 5 − 1 0 − 3 → 1 0 0 − 1 1 0 0 − 1 3 : : : 1 1 3 − 1 1 − 3 → 1 0 0 0 1 0 0 0 1 : : : 3 2 1 − 1 0 − 1 所以
X = 3 2 1 − 1 0 − 1
18 设
α 1 = ( 1 , 1 , 1 ) α 2 = ( 1 , 2 , 3 ) α 3 = ( 1 , 3 , t )
(1) 问当
t α 1 , α 2 , α 3
(2) 问当
t α 1 , α 2 , α 3
(3) 当向量组
α 1 , α 2 , α 3 α 3 α 1 α 2
【答案】 t = 5 α 1 , α 2 , α 3 t = 5 α 1 , α 2 , α 3 t = 5 α 3 = − α 1 + 2 α 2
【解析】 A = [ α 1 , α 2 , α 3 ] = 1 1 1 1 2 3 1 3 t
det ( A ) = 1 ⋅ ( 2 t − 9 ) − 1 ⋅ ( t − 3 ) + 1 ⋅ ( 3 − 2 ) = 2 t − 9 − t + 3 + 1 = t − 5.
当
det ( A ) = 0 t = 5 det ( A ) = 0 t = 5 t = 5 α 3 = a α 1 + b α 2
( 1 , 3 , 5 ) = a ( 1 , 1 , 1 ) + b ( 1 , 2 , 3 ) ,
解得方程组:
由前两个方程得
b = 2 a = − 1 α 3 = − α 1 + 2 α 2
19 设
A = − 1 2 2 2 − 1 − 2 2 − 2 − 1 .
(1) 试求矩阵
A
(2) 利用(I)小题的结果,求矩阵
E + A − 1 E 3
【答案】 A 1 − 5 E + A − 1 2 5 4
【解析】 A
∣ λ E − A ∣ = λ + 1 − 2 − 2 − 2 λ + 1 2 − 2 2 λ + 1 = λ − 1 − λ − 1 0 − 2 λ + 1 2 − 2 2 λ + 1
= λ − 1 0 0 − 2 λ + 3 2 − 2 4 λ + 1 = ( λ − 1 ) λ + 3 2 4 λ + 1 = ( λ − 1 ) 2 ( λ + 5 ) , 故矩阵
A 1 , 1 , − 5
(Ⅱ) 设
λ A α A α = λ α
( E + A − 1 ) α = ( 1 + λ 1 ) α
即
1 + λ 1 E + A − 1 A 1 , 1 , − 5 E + A − 1 2 , 2 , 5 4
20 已知随机变量
X Y
f ( x , y ) = { e − ( x + y ) , 0 , 0 < x < + ∞ , 0 < y < + ∞ , 其他 .
试求:
(1)
P { X < Y }
(2)
E ( X Y )
【答案】 P { X < Y } = 2 1 E ( X Y ) = 1
【解析】
P { X < Y } = ∬ x < y f ( x , y ) d x d y = ∫ 0 + ∞ e − y d y ∫ 0 y e − x d x = ∫ 0 + ∞ e − y ( 1 − e − y ) d y = [ − e − y + 2 1 e − 2 y ] 0 + ∞ = 2 1 .
(Ⅱ) 由二维连续型随机变量的数学期望定义得
E ( X Y ) = ∫ − ∞ + ∞ ∫ − ∞ + ∞ x y f ( x , y ) d x d y = ∫ 0 + ∞ ∫ 0 + ∞ x y e − ( x + y ) d x d y = ∫ 0 + ∞ x e − x d x ⋅ ∫ 0 + ∞ y e − y d y .
由分部积分法有
∫ 0 + ∞ y e − y d y = − ∫ 0 + ∞ y d ( e − y ) = [ − y e − y ] 0 + ∞ + ∫ 0 + ∞ e − y d y = [ − y e − y ] 0 + ∞ + [ − e − y ] 0 + ∞ .
由洛必达法则,对
∞ ∞
y → + ∞ lim y e − y = y → + ∞ lim e y 1 = 0.
所以有
E ( X Y ) = 1
21 设随机变量
X [ 2 , 5 ] X 3
【答案】
27 20
【解析】
随机变量
X [ 2 , 5 ] f ( x ) = 3 1 3
P ( X > 3 ) = 5 − 2 5 − 3 = 3 2 .
进行三次独立观测,将每次观测视为一次伯努利试验,其中“成功”定义为观测值大于
3 p = 3 2 Y Y Y ∼ Binomial ( n = 3 , p = 3 2 )
P ( Y ≥ 2 ) = P ( Y = 2 ) + P ( Y = 3 ) .
计算如下:
P ( Y = 2 ) = ( 2 3 ) ( 3 2 ) 2 ( 3 1 ) 1 = 3 × 9 4 × 3 1 = 27 12 = 9 4 ,
P ( Y = 3 ) = ( 3 3 ) ( 3 2 ) 3 ( 3 1 ) 0 = 1 × 27 8 × 1 = 27 8 .
因此,
P ( Y ≥ 2 ) = 9 4 + 27 8 = 27 12 + 27 8 = 27 20 .