卷 5 填空题 本题满分15分,每小题3分
1 同试卷 4 第 1 题
2 某商品的需求量
Q p Q = a p b a b a = 0 p
【答案】
b
【解析】 需求的价格弹性定义为
E p = d p d Q ⋅ Q p Q = a p b a b a = 0 d p d Q = ab p b − 1 E p = ( ab p b − 1 ) ⋅ a p b p = b ⋅ p b p b = b p b
3 行列式
1 1 1 x + 1 − 1 − 1 x − 1 − 1 1 x + 1 1 1 x − 1 − 1 − 1 − 1
【答案】
x 4
【解析】
1 0 0 x − 1 0 x 0 1 x 0 0 x − 1 − x − x − x 然后,从第四行减去
x
1 0 0 0 − 1 0 x x 1 x 0 − x x − 1 − x − x − x 2 沿第一列展开,行列式等于其余子式的行列式:
计算该三阶行列式,按第一行展开:
0 ⋅ 0 − x − x − x 2 − x ⋅ x x − x − x 2 + ( − x ) ⋅ x x 0 − x 其中,
x x − x − x 2 = x ⋅ ( − x 2 ) − ( − x ) ⋅ x = − x 3 + x 2
代入得:
− x ⋅ ( − x 3 + x 2 ) + ( − x ) ⋅ ( − x 2 ) = x ⋅ ( x 3 − x 2 ) + x ⋅ x 2 = x 4 − x 3 + x 3 = x 4
因此,原行列式为
x 4
4 设随机变量
X 1 , X 2 , X 3 X 1 [ 0 , 6 ] X 2 N ( 0 , 2 2 ) X 3 λ = 3 Y = X 1 − 2 X 2 + 3 X 3 D Y =
【答案】
46
【解析】
由于随机变量
X 1 , X 2 , X 3 Y = X 1 − 2 X 2 + 3 X 3 D Y = Var ( Y ) = 1 2 ⋅ Var ( X 1 ) + ( − 2 ) 2 ⋅ Var ( X 2 ) + 3 2 ⋅ Var ( X 3 )
计算各变量的方差:
X 1 [ 0 , 6 ] Var ( X 1 ) = 12 ( 6 − 0 ) 2 = 12 36 = 3 X 2 N ( 0 , 2 2 ) Var ( X 2 ) = 2 2 = 4 X 3 λ = 3 Var ( X 3 ) = 3 代入公式:
D Y = 1 2 ⋅ 3 + ( − 2 ) 2 ⋅ 4 + 3 2 ⋅ 3 = 1 ⋅ 3 + 4 ⋅ 4 + 9 ⋅ 3 = 3 + 16 + 27 = 46.
因此,
D Y = 46
5 同试卷 4 第 4 题
选择题 本题满分15分,每小题3分
6 同试卷 4 第 6 题
7 同试卷 4 第 7 题
8 同试卷 1 第 10 题
9 设
n A X = 0 A r A X = 0
查看答案与解析
正确答案:B n A X = 0 A r r n r = n A r < n A r = n r ≥ n r ≤ n r = n r > n r n
10 同试卷 4 第 10 题
计算题 本题满分20分,每小题5分
11 求极限
lim x → + ∞ ( x + e x ) x 1
【答案】 e
【解析】 lim x → + ∞ ( x + e x ) x 1 L = lim x → + ∞ ( x + e x ) x 1 ln L = lim x → + ∞ x l n ( x + e x ) e x x + e x e x ( 1 + e x x ) ln ( x + e x ) = ln e x + ln ( 1 + e x x ) = x + ln ( 1 + e x x )
ln L = x → + ∞ lim x x + ln ( 1 + e x x ) = x → + ∞ lim ( 1 + x ln ( 1 + e x x ) ) .
当
x → + ∞ e x x → 0 ln ( 1 + e x x ) ∼ e x x
x ln ( 1 + e x x ) ∼ x e x x = e x 1 → 0.
因此,
ln L = 1 L = e e
12 已知
z = a x 2 − y 2 a > 0 a = 1 d z
【答案】
d z = x 2 − y 2 a x 2 − y 2 ln a ( x d x − y d y ) 【解析】
给定函数
z = a x 2 − y 2 a > 0 a = 1 d z d z = ∂ x ∂ z d x + ∂ y ∂ z d y
首先,令
u = x 2 − y 2 z = a u u
∂ x ∂ u = x 2 − y 2 x , ∂ y ∂ u = − x 2 − y 2 y . 对
z u
利用链式法则,求
z x y
∂ x ∂ z = ∂ u ∂ z ⋅ ∂ x ∂ u = a x 2 − y 2 ln a ⋅ x 2 − y 2 x ,
∂ y ∂ z = ∂ u ∂ z ⋅ ∂ y ∂ u = a x 2 − y 2 ln a ⋅ ( − x 2 − y 2 y ) = − x 2 − y 2 a x 2 − y 2 ln a ⋅ y . 代入全微分公式:
d z = ∂ x ∂ z d x + ∂ y ∂ z d y = x 2 − y 2 a x 2 − y 2 ln a ⋅ x d x − x 2 − y 2 a x 2 − y 2 ln a ⋅ y d y , 整理得:
d z = x 2 − y 2 a x 2 − y 2 ln a ( x d x − y d y ) . 注意:此结果在
x 2 − y 2 > 0
13 求不定积分
∫ x 2 x + l n ( 1 − x ) d x
【答案】
− x ( 1 − x ) ln ( 1 − x ) + C
【解析】
首先,将原积分拆分为两个部分:
∫ x 2 x + ln ( 1 − x ) d x = ∫ x 2 x d x + ∫ x 2 ln ( 1 − x ) d x = ∫ x 1 d x + ∫ x 2 ln ( 1 − x ) d x
其中,
∫ x 1 d x = ln ∣ x ∣ + C 1
对于
∫ x 2 l n ( 1 − x ) d x u = ln ( 1 − x ) d v = x 2 1 d x d u = − 1 − x 1 d x v = − x 1
∫ u d v = uv − ∫ v d u
得到:
∫ x 2 ln ( 1 − x ) d x = ln ( 1 − x ) ⋅ ( − x 1 ) − ∫ ( − x 1 ) ⋅ ( − 1 − x 1 ) d x = − x ln ( 1 − x ) − ∫ x ( 1 − x ) 1 d x
对
∫ x ( 1 − x ) 1 d x
x ( 1 − x ) 1 = x 1 + 1 − x 1
所以:
∫ x ( 1 − x ) 1 d x = ∫ x 1 d x + ∫ 1 − x 1 d x = ln ∣ x ∣ − ln ∣1 − x ∣ + C 2
代回分部积分结果:
∫ x 2 ln ( 1 − x ) d x = − x ln ( 1 − x ) − ( ln ∣ x ∣ − ln ∣1 − x ∣ ) + C 2 = − x ln ( 1 − x ) − ln ∣ x ∣ + ln ∣1 − x ∣ + C 2
将两部分积分合并:
∫ x 2 x + ln ( 1 − x ) d x = ln ∣ x ∣ + ( − x ln ( 1 − x ) − ln ∣ x ∣ + ln ∣1 − x ∣ ) + C = ln ∣1 − x ∣ − x ln ( 1 − x ) + C
由于
ln ( 1 − x ) 1 − x > 0 x < 1
ln ( 1 − x ) − x ln ( 1 − x ) + C = − x ( 1 − x ) ln ( 1 − x ) + C
此结果验证无误,求导后可得原被积函数。
14 求二重积分
∬ D 1 + x 2 + y 2 1 − x 2 − y 2 d x d y D x 2 + y 2 = 1 x = 0 y = 0
【答案】
2 π ln 2 − 4 π
【解析】
积分区域
D 0 ≤ θ ≤ 2 π 0 ≤ r ≤ 1 x = r cos θ y = r sin θ x 2 + y 2 = r 2 d x d y = r d r d θ 1 + r 2 1 − r 2
∬ D 1 + x 2 + y 2 1 − x 2 − y 2 d x d y = ∫ 0 π /2 ∫ 0 1 1 + r 2 1 − r 2 r d r d θ
由于被积函数与
θ
= ∫ 0 π /2 d θ ⋅ ∫ 0 1 1 + r 2 1 − r 2 r d r
计算
θ
∫ 0 π /2 d θ = 2 π
计算
r I r = ∫ 0 1 1 + r 2 1 − r 2 r d r u = r 2 d u = 2 r d r r d r = 2 d u u = 0 u = 1
I r = ∫ 0 1 1 + u 1 − u ⋅ 2 d u = 2 1 ∫ 0 1 1 + u 1 − u d u
简化被积函数:
1 + u 1 − u = − 1 + 1 + u 2
因此:
∫ 0 1 1 + u 1 − u d u = ∫ 0 1 ( − 1 + 1 + u 2 ) d u = [ − u ] 0 1 + 2 [ ln ∣1 + u ∣ ] 0 1 = − 1 + 2 ln 2
于是:
I r = 2 1 ( − 1 + 2 ln 2 ) = − 2 1 + ln 2
二重积分为:
2 π × I r = 2 π ( − 2 1 + ln 2 ) = 2 π ln 2 − 4 π
故所求积分为
2 π ln 2 − 4 π
解答题 15 已知某企业的总收入函数为
R = 26 x − 2 x 2 − 4 x 3 C = 8 x + x 2 x
【答案】 L = 18 x − 3 x 2 − 4 x 3 MR = 26 − 4 x − 12 x 2 MC = 8 + 2 x x = 1 L = 11
【解析】
L = R − C = ( 26 x − 2 x 2 − 4 x 3 ) − ( 8 x + x 2 ) = 18 x − 3 x 2 − 4 x 3
边际收入函数是总收入函数对产量
x
MR = d x d R = 26 − 4 x − 12 x 2
边际成本函数是总成本函数对产量
x
MC = d x d C = 8 + 2 x
为了求最大利润时的产量,对利润函数求一阶导数并设为零:
d x d L = 18 − 6 x − 12 x 2 = 0
简化得
2 x 2 + x − 3 = 0
解二次方程得
x = 1 x = − 1.5 x = 1
d x 2 d 2 L = − 6 − 24 x
在
x = 1 − 30 < 0 x = 1
L = 18 ( 1 ) − 3 ( 1 ) 2 − 4 ( 1 ) 3 = 11
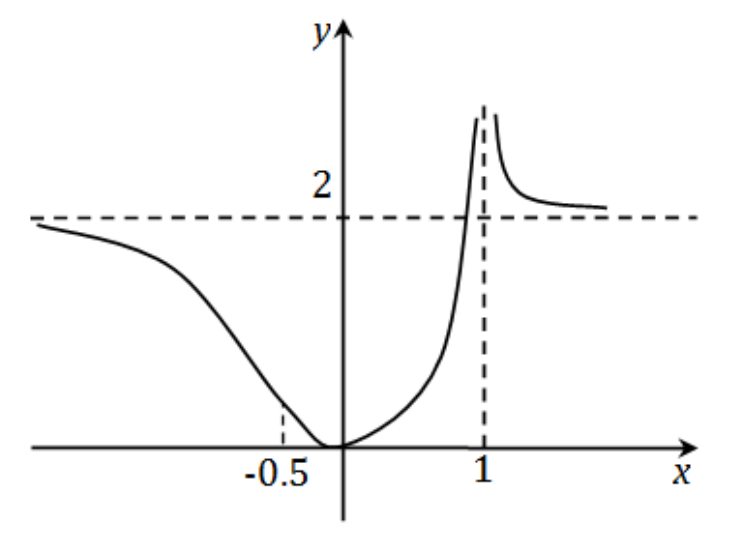
16 已知函数
y = ( 1 − x ) 2 2 x 2
【答案】
单调区间:在
( − ∞ , 0 ) ( 1 , + ∞ ) ( 0 , 1 ) 极值点:局部极小值点为
( 0 , 0 ) 凹凸性:在
( − ∞ , − 2 1 ) ( − 2 1 , 1 ) ( 1 , + ∞ ) 拐点:
( − 2 1 , 9 2 ) 渐近线:垂直渐近线为
x = 1 y = 2 函数图形:见解析 【解析】
函数
y = ( 1 − x ) 2 2 x 2 ( − ∞ , 1 ) ∪ ( 1 , + ∞ )
一阶导数为
y ′ = ( 1 − x ) 3 4 x .
令
y ′ = 0 x = 0
当
x < 0 y ′ < 0 当
0 < x < 1 y ′ > 0 当
x > 1 y ′ < 0 因此,单调区间为
( − ∞ , 0 ) ( 0 , 1 ) ( 1 , + ∞ ) ( 0 , 0 )
二阶导数为
y ′′ = ( 1 − x ) 4 4 ( 1 + 2 x ) .
令
y ′′ = 0 x = − 2 1
当
x < − 2 1 y ′′ < 0 当
x > − 2 1 x = 1 y ′′ > 0 因此,凹凸性为
( − ∞ , − 2 1 ) ( − 2 1 , 1 ) ( 1 , + ∞ ) ( − 2 1 , 9 2 )
渐近线:
垂直渐近线为
x = 1 lim x → 1 y = + ∞ 水平渐近线为
y = 2 lim x → ± ∞ y = 2 图形基于以上性质绘制:经过点
( 0 , 0 ) ( − 2 1 , 9 2 ) x = 1 y = 2
当
x → − ∞ y = 2 当
x → 1 − + ∞ 当
x → 1 + + ∞ 当
x → + ∞ y = 2 17 同试卷 4 第 17 题
18 同试卷 4 第 18 题
19 同试卷 4 第 19 题
20 已知随机变量
X Y
( x , y ) P { X = x , Y = y } ( 0 , 0 ) 0.10 ( 0 , 1 ) 0.15 ( 1 , 0 ) 0.25 ( 1 , 1 ) 0.20 ( 2 , 0 ) 0.15 ( 2 , 1 ) 0.15
试求:
(1)
X
(2)
X + Y
(3)
Z = sin 2 π ( X + Y )
【答案】 X
X P { X = x } 0 0.25 1 0.45 2 0.30
(2)
X + Y
X + Y P { X + Y = s } 0 0.10 1 0.40 2 0.35 3 0.15
(3)
Z = sin 2 π ( X + Y ) EZ = 0.25
【解析】 X X X = 0 P ( X = 0 ) = P ( 0 , 0 ) + P ( 0 , 1 ) = 0.10 + 0.15 = 0.25 X = 1 P ( X = 1 ) = P ( 1 , 0 ) + P ( 1 , 1 ) = 0.25 + 0.20 = 0.45 X = 2 P ( X = 2 ) = P ( 2 , 0 ) + P ( 2 , 1 ) = 0.15 + 0.15 = 0.30 X
(2) 求
X + Y X + Y X + Y = 0 ( 0 , 0 ) 0.10 X + Y = 1 ( 0 , 1 ) ( 1 , 0 ) 0.15 + 0.25 = 0.40 X + Y = 2 ( 1 , 1 ) ( 2 , 0 ) 0.20 + 0.15 = 0.35 X + Y = 3 ( 2 , 1 ) 0.15 X + Y
(3) 求
Z = sin 2 π ( X + Y ) S = X + Y Z = sin 2 π S S Z S = 0 Z = sin ( 0 ) = 0 S = 1 Z = sin ( π /2 ) = 1 S = 2 Z = sin ( π ) = 0 S = 3 Z = sin ( 3 π /2 ) = − 1 S E [ Z ] = 0 × P ( S = 0 ) + 1 × P ( S = 1 ) + 0 × P ( S = 2 ) + ( − 1 ) × P ( S = 3 ) = 0 × 0.10 + 1 × 0.40 + 0 × 0.35 + ( − 1 ) × 0.15 = 0.40 − 0.15 = 0.25 0.25
21 某仪器装有三只独立工作的同型号电子元件,其寿命(单位:小时)都服从同一指数分布,分布密度为
f ( x ) = { 600 1 e − x /600 , 0 , x > 0 , x ≤ 0.
试求:在仪器使用的最初
200 α
【答案】 α = 1 − e − 1
【解析】 λ = 600 1
p = F ( 200 ) = 1 − e − λ ⋅ 200 = 1 − e − 600 200 = 1 − e − 3 1
单个元件在 200 小时内存活的概率为
1 − p = e − 3 1
( e − 3 1 ) 3 = e − 1
因此,在 200 小时内至少有一只电子元件损坏的概率为:
α = 1 − e − 1