卷 1
填空题
本题满分15分,每小题3分
1
过点
M(1,2,−1)
且与直线
⎩⎨⎧x=−t+2,y=3t−4,z=t−1
垂直的平面方程是 ______.
【答案】
−x+3y+z−4=0
(或等价形式
x−3y−z+4=0
)
【解析】
首先,从直线的参数方程
⎩⎨⎧x=−t+2,y=3t−4,z=t−1
中,提取方向向量
d=(−1,3,1)
。由于所求平面与直线垂直,平面的法向量
n
与方向向量
d
平行,故取
n=(−1,3,1)
。
平面过点
M(1,2,−1)
,使用点法式方程:
n⋅(r−r0)=0
,其中
r=(x,y,z)
,
r0=(1,2,−1)
。代入得:
−1(x−1)+3(y−2)+1(z−(−1))=0
简化:
−x+1+3y−6+z+1=0
−x+3y+z−4=0
因此,所求平面方程为
−x+3y+z−4=0
。
2
设
a
为非零常数,则
limx→∞(x−ax+a)x=
______.
【答案】
e2a
【解析】
考虑极限
limx→∞(x−ax+a)x
。将分式改写为:
x−ax+a=1+x−a2a
于是极限化为:
x→∞lim(1+x−a2a)x
令
t=x−a
,则当
x→∞
时
t→∞
,且
x=t+a
。代入得:
(1+t2a)t+a=(1+t2a)t⋅(1+t2a)a
取极限:
t→∞lim(1+t2a)t⋅t→∞lim(1+t2a)a
其中
limt→∞(1+t2a)t=e2a
,且
limt→∞(1+t2a)a=1a=1
。
因此,极限为
e2a
。
3
设函数
f(x)={1,0,∣x∣≤1,∣x∣>1,
则
f[f(x)]=
______.
【答案】
1
【解析】
函数
f(x)
定义为:当
∣x∣≤1
时,
f(x)=1
;当
∣x∣>1
时,
f(x)=0
。
考虑复合函数
f[f(x)]
,即以内层函数
f(x)
的值作为外层函数
f
的输入。
由于
f(x)
的值只能是 0 或 1,且无论输入是 0 还是 1,均有
∣0∣=0≤1
和
∣1∣=1≤1
,因此外层函数
f
的输出始终为 1。
即,对于任意
x
,有
f[f(x)]=1
。
4
积分
∫02dx∫x2e−y2dy
的值等于 ______.
【答案】
21(1−e−4)
【解析】
给定二重积分
∫02dx∫x2e−y2dy
,直接计算内层积分较困难,因此考虑改变积分顺序。积分区域由
0≤x≤2
和
x≤y≤2
定义,这等价于
0≤y≤2
和
0≤x≤y
。改变积分顺序后,积分变为:
∫02dy∫0ye−y2dx
计算内层积分:
∫0ye−y2dx=e−y2∫0ydx=ye−y2
因此,积分化为:
∫02ye−y2dy
令
u=y2
,则
du=2ydy
,即
ydy=2du
。当
y=0
时,
u=0
;当
y=2
时,
u=4
。代入得:
∫02ye−y2dy=∫04e−u⋅2du=21∫04e−udu=21[−e−u]04=21(−e−4+1)=21(1−e−4)
故积分值为
21(1−e−4)
。
5
已知向量组
α1=(1,2,3,4)
,
α2=(2,3,4,5)
,
α3=(3,4,5,6)
,
α4=(4,5,6,7)
,
则该向量组的秩是______.
【答案】
2
【解析】
给定向量组
α1=(1,2,3,4)
,
α2=(2,3,4,5)
,
α3=(3,4,5,6)
,
α4=(4,5,6,7)
。
构造矩阵
A=1234234534564567
,通过行变换化为行阶梯形:
首先,
R2−2R1
、
R3−3R1
、
R4−4R1
,得到
10002−1−2−33−2−4−64−3−6−9
。
然后,
R2×(−1)
,得到
100021−2−332−4−643−6−9
。
接着,
R3+2R2
、
R4+3R2
,得到
1000210032004300
。
行阶梯形中有两个非零行,因此矩阵的秩为2,即向量组的秩为2。
此外,直观上,每个向量均可由
α1
和
(1,1,1,1)
线性表示,故向量组张成的空间是二维的,秩为2。
选择题
本题满分15分,每小题3分
6
设
f(x)
是连续函数,且
F(x)=∫xe−xf(t)dt
,则
F′(x)
等于
正确答案:A
【解析】 给定
F(x)=∫xe−xf(t)dt
,其中
f(x)
是连续函数。根据微积分的基本定理和链式法则,对于积分上限和下限均为
x
的函数的情况,有
F′(x)=f(g(x))⋅g′(x)−f(h(x))⋅h′(x)
,其中
g(x)=e−x
,
h(x)=x
。计算得
g′(x)=−e−x
,
h′(x)=1
。代入公式得
F′(x)=f(e−x)⋅(−e−x)−f(x)⋅1=−e−xf(e−x)−f(x)
,与选项 A 一致。
7
已知函数
f(x)
具有任意阶导数,且
f′(x)=[f(x)]2
,
则当
n
为大于
2
的正整数时,
f(x)
的
n
阶导数
f(n)(x)
是
正确答案:A【解析】 已知函数
f(x)
满足
f′(x)=[f(x)]2
。通过求高阶导数,观察模式:
- 一阶导数:
f′(x)=[f(x)]2=1!⋅[f(x)]1+1
- 二阶导数:
f′′(x)=dxd[f′(x)]=dxd[f(x)]2=2f(x)f′(x)=2f(x)⋅[f(x)]2=2[f(x)]3=2!⋅[f(x)]2+1
- 三阶导数:
f′′′(x)=dxd[f′′(x)]=dxd[2[f(x)]3]=2⋅3[f(x)]2f′(x)=6[f(x)]2⋅[f(x)]2=6[f(x)]4=3!⋅[f(x)]3+1
由此归纳,对于任意正整数
n
,有
f(n)(x)=n!⋅[f(x)]n+1
。当
n>2
时,该公式同样成立。选项 A 与此一致,其他选项均不匹配。
8
设
α
为常数,则级数
∑n=1∞[n2sinnα−n1]
正确答案:C【解析】 级数
∑n=1∞[n2sinnα−n1]
由两部分组成。第一部分
∑n=1∞n2sinnα
由于
∣sinnα∣≤1
,有
n2sinnα≤n21
,而
∑n21
收敛(p-级数,p=2>1),因此该部分绝对收敛,且收敛性与
α
无关。第二部分
∑n=1∞−n1=−∑n=1∞n1/21
是 p-级数,p=1/2<1,因此发散。由于一个收敛级数与一个发散级数的和发散,故原级数发散,且与
α
的取值无关。因此选项 C 正确。
9
已知
f(x)
在
x=0
的某个邻域内连续,且
f(0)=0
,
limx→01−cosxf(x)=2
,
则在点
x=0
处
f(x)
正确答案:D
【解析】 已知
limx→01−cosxf(x)=2
且
f(0)=0
。由于
1−cosx∼2x2
当
x→0
,代入极限得
limx→02x2f(x)=2
,即
limx→0x2f(x)=1
。因此,
f(x)∼x2
在
x=0
附近。
考虑导数:
f′(0)=limh→0hf(h)−f(0)=limh→0hf(h)
。由
f(h)∼h2
,得
hf(h)∼h→0
,故
f′(0)=0
,即可导且导数为零,排除 A 和 B。
由
limx→0x2f(x)=1>0
,知在
x=0
某邻域内
f(x)>0
对于
x=0
,而
f(0)=0
,故
f(x)
在
x=0
处取得极小值,排除 C。因此正确答案为 D。
10
已知
β1
,
β2
是非齐次线性方程组
AX=b
的两个不同的解,
α1
,
α2
是对应齐次线性方程组
AX=0
的基础解系,
k1
,
k2
为任意常数,则方程组
AX=b
的通解(一般解)必是
正确答案:B【解析】
非齐次线性方程组
AX=b
的通解由对应齐次方程组
AX=0
的通解和一个特解组成。
已知
α1
和
α2
是
AX=0
的基础解系,因此齐次通解为
k1α1+k2α2,
其中
k1
、
k2
为任意常数。
选项 B:
齐次部分为
k1α1+k2(α1−α2)=(k1+k2)α1+(−k2)α2,
由于
k1
和
k2
任意,该形式能覆盖整个齐次解空间。
特解部分为
(β1+β2)/2
,验证得
A[2β1+β2]=2Aβ1+Aβ2=2b+b=b,
因此是特解。
选项 A:
特解
(β1−β2)/2
是齐次解而非特解。
选项 C:
齐次部分包含
β1+β2
,它不是齐次解。
选项 D:
齐次部分可能不能覆盖整个齐次解空间,因为
β1−β2
可能与
α1
线性相关。
故 B 正确。
计算题
本题满分15分,每小题5分
11
求
∫01(2−x)2ln(1+x)dx
.
【答案】
3ln2
【解析】
考虑积分
I=∫01(2−x)2ln(1+x)dx
。使用分部积分法,设
u=ln(1+x)
,则
du=1+x1dx
;设
dv=(2−x)21dx
,则
v=2−x1
。于是:
I=[ln(1+x)⋅2−x1]01−∫012−x1⋅1+x1dx
计算边界项:
当
x=1
时,
ln(2)⋅2−11=ln2
;当
x=0
时,
ln(1)⋅2−01=0
,故边界项为
ln2
。因此:
I=ln2−∫01(2−x)(1+x)1dx
现在计算积分
J=∫01(2−x)(1+x)1dx
。使用部分分式分解:
(2−x)(1+x)1=2−xA+1+xB
两边乘以
(2−x)(1+x)
得:
1=A(1+x)+B(2−x)
代入
x=2
得
1=3A
,故
A=31
;代入
x=0
得
1=A+2B
,即
1=31+2B
,解得
B=31
。因此:
J=∫01(2−x1/3+1+x1/3)dx=31∫012−x1dx+31∫011+x1dx
计算第一积分:令
u=2−x
,则
du=−dx
,积分限变为
u=2
到
u=1
,故:
∫012−x1dx=∫21u1(−du)=∫12u1du=lnu12=ln2 第二积分:
∫011+x1dx=ln(1+x)01=ln2 所以
J=31ln2+31ln2=32ln2
。代入原式:
I=ln2−32ln2=31ln2
故积分为
3ln2
。
12
设
z=f(2x−y,ysinx)
,其中
f(u,v)
具有连续的二阶偏导数,求
∂x∂y∂2z
.
【答案】
∂x∂y∂2z=−2fuu+(2sinx−ycosx)fuv+cosxfv+ysinxcosxfvv
其中
fuu,fuv,fvv
分别表示
f
对
u
和
v
的二阶偏导数。
【解析】
设
u=2x−y
,
v=ysinx
,则
z=f(u,v)
。首先求一阶偏导数
∂y∂z
:
∂y∂z=∂u∂f⋅∂y∂u+∂v∂f⋅∂y∂v=fu⋅(−1)+fv⋅sinx=−fu+sinxfv.
然后求混合偏导数
∂x∂y∂2z=∂x∂(∂y∂z)
:
∂x∂y∂2z=∂x∂(−fu)+∂x∂(sinxfv)=−∂x∂(fu)+cosxfv+sinx⋅∂x∂(fv).
计算
∂x∂(fu)
和
∂x∂(fv)
使用链式法则:
∂x∂(fu)=∂u∂fu⋅∂x∂u+∂v∂fu⋅∂x∂v=fuu⋅2+fuv⋅(ycosx)=2fuu+ycosxfuv,
∂x∂(fv)=∂u∂fv⋅∂x∂u+∂v∂fv⋅∂x∂v=fvu⋅2+fvv⋅(ycosx)=2fuv+ycosxfvv( fuv=fvu).
代入得:
∂x∂y∂2z=−(2fuu+ycosxfuv)+cosxfv+sinx⋅(2fuv+ycosxfvv)=−2fuu−ycosxfuv+cosxfv+2sinxfuv+ysinxcosxfvv.
合并同类项:
∂x∂y∂2z=−2fuu+(2sinx−ycosx)fuv+cosxfv+ysinxcosxfvv.
13
求微分方程
y′′+4y′+4y=e−2x
的通解(一般解).
【答案】
y=e−2x(C1+C2x+21x2)
其中
C1
和
C2
为任意常数。
【解析】
给定微分方程
y′′+4y′+4y=e−2x
是二阶线性非齐次方程。通解由齐次解和特解组成。
首先求齐次解。齐次方程
y′′+4y′+4y=0
的特征方程为
r2+4r+4=0
,解得重根
r=−2
,因此齐次解为
yh=(C1+C2x)e−2x
,其中
C1
和
C2
为常数。
然后求特解。由于非齐次项
e−2x
与齐次解形式重叠,特解假设为
yp=Ax2e−2x
。代入原方程求待定常数
A
。计算一阶导数
yp′=Ae−2x(2x−2x2)
和二阶导数
yp′′=Ae−2x(4x2−8x+2)
。代入原方程得:
yp′′+4yp′+4yp=Ae−2x(4x2−8x+2)+4Ae−2x(2x−2x2)+4Ax2e−2x=2Ae−2x
令其等于非齐次项
e−2x
,有
2A=1
,解得
A=21
。因此特解为
yp=21x2e−2x
.
最终通解为齐次解与特解之和:
y=yh+yp=(C1+C2x)e−2x+21x2e−2x=e−2x(C1+C2x+21x2)
解答题
14
求幂级数
∑n=0∞(2n+1)xn
的收敛域,并求其和函数.
【答案】
收敛域为
(−1,1)
,和函数为
S(x)=(1−x)21+x
。
【解析】
考虑幂级数
∑n=0∞(2n+1)xn
。使用比值判别法求收敛域:
设
an=(2n+1)xn
,则
n→∞limanan+1=n→∞lim(2n+1)xn(2n+3)xn+1=n→∞lim2n+12n+3∣x∣=∣x∣. 当
∣x∣<1
时级数收敛,当
∣x∣>1
时级数发散。
在端点
x=1
处,级数为
∑n=0∞(2n+1)
,通项不趋于零,发散;
在
x=−1
处,级数为
∑n=0∞(2n+1)(−1)n
,通项不趋于零,发散。
因此收敛域为
(−1,1)
。
求和函数时,将级数写为:
S(x)=n=0∑∞(2n+1)xn=2n=0∑∞nxn+n=0∑∞xn.
其中
∑n=0∞xn=1−x1
(对于
∣x∣<1
),
且
∑n=0∞nxn=(1−x)2x
(因为
∑n=1∞nxn−1=(1−x)21
,故
∑n=1∞nxn=(1−x)2x
,且
n=0
时项为零)。
代入得:
S(x)=2⋅(1−x)2x+1−x1=(1−x)22x+(1−x)21−x=(1−x)22x+1−x=(1−x)21+x.
因此和函数为
S(x)=(1−x)21+x
(对于
∣x∣<1
)。
15
求曲面积分
I=∬Syzdxdx+2dxdy
,其中
S
是球面
x2+y2+z2=4
外侧在
z≥0
的部分.
【答案】
12π
【解析】
考虑曲面积分
I=∬Syzdzdx+2dxdy
,其中
S
是球面
x2+y2+z2=4
外侧在
z≥0
的部分。这里将原积分中的
dxdx
视为
dzdx
的笔误,对应向量场
F=(0,yz,2)
。
使用散度定理,引入圆盘
D:x2+y2≤4,z=0
方向向下,与
S
构成封闭曲面
S′=S∪D
,包围上半球体
V:x2+y2+z2≤4,z≥0
。则
计算散度:
∇⋅F=∂x∂(0)+∂y∂(yz)+∂z∂(2)=z. 在球坐标下,
x=ρsinϕcosθ
,
y=ρsinϕsinθ
,
z=ρcosϕ
,其中
ρ∈[0,2]
,
ϕ∈[0,π/2]
,
θ∈[0,2π]
,体积元
dV=ρ2sinϕdρdϕdθ
。于是
∭VzdV=∫02π∫0π/2∫02ρcosϕ⋅ρ2sinϕdρdϕdθ=2π⋅21⋅4=4π.
在圆盘
D
上,
z=0
,法向量向下,
F⋅dS=(0,0,2)⋅(0,0,−1)dS=−2dS, 所以
因此,
∬SF⋅dS=∭VzdV−∬DF⋅dS=4π−(−8π)=12π. 故曲面积分
I=12π
.
16
设不恒为常数的函数
f(x)
在闭区间
[a,b]
上连续,在开区间
(a,b)
内可导,
且
f(a)=f(b)
.证明在
(a,b)
内至少存在一点
ξ
,使得
f′(ξ)>0
.
【答案】 见解析
【解析】
由于
f(x)
在闭区间
[a,b]
上不恒为常数,且
f(a)=f(b)
,故存在一点
c∈(a,b)
,使得
f(c)=f(a)
。考虑两种情况:
若
f(c)>f(a)
,则在区间
[a,c]
上应用拉格朗日中值定理,存在
ξ∈(a,c)⊂(a,b)
,使得
f′(ξ)=c−af(c)−f(a)>0
若
f(c)<f(a)
,则在区间
[c,b]
上应用拉格朗日中值定理,存在
ξ∈(c,b)⊂(a,b)
,使得
f′(ξ)=b−cf(b)−f(c)=b−cf(a)−f(c)>0
综上,在
(a,b)
内至少存在一点
ξ
,使得
f′(ξ)>0
。
17
设四阶矩阵
B=1000−11000−11000−11
,
C=2000120031204312
,
且矩阵
A
满足关系式
A(E−C−1B)′C′=E
,其中
E
为四阶单位矩阵,
C−1
表示
C
的逆矩阵,
C′
表示
C
的转置矩阵,将上述关系式化简并求矩阵
A
.
【答案】
A=1−21001−21001−20001 【解析】
给定关系式
A(E−C−1B)′C′=E
,其中
E
为单位矩阵。
首先,简化关系式:
(E−C−1B)′=E′−(C−1B)′=E−B′(C−1)′=E−B′(C′)−1,
代入得:
A[E−B′(C′)−1]C′=E.
计算括号内与
C′
的乘积:
[E−B′(C′)−1]C′=EC′−B′(C′)−1C′=C′−B′E=C′−B′.
因此,关系式简化为
A(C′−B′)=E,
所以
A=(C′−B′)−1.
计算
B′
和
C′
:
B=1000−11000−11000−11,B′=1−10001−10001−10001. C=2000120031204312,C′=2134021300210002. 计算
C′−B′
:
C′−B′=2−11−(−1)3−04−00−02−11−(−1)3−00−00−02−11−(−1)0−00−00−02−1=1234012300120001.
求
(C′−B′)−1
:
设
D=C′−B′=1234012300120001
,求
D−1
。
设
D−1=x11x21x31x410x22x32x4200x33x43000x44
,解
DD−1=E
:
第一行:
1⋅x11=1
,得
x11=1
。
第二行:
2⋅x11+1⋅x21=0
,即
2⋅1+x21=0
,得
x21=−2
;
2⋅x12+1⋅x22=1
,但
x12=0
,得
x22=1
。
第三行:
3⋅x11+2⋅x21+1⋅x31=0
,即
3⋅1+2⋅(−2)+x31=0
,得
x31=1
;
3⋅x12+2⋅x22+1⋅x32=0
,即
0+2⋅1+x32=0
,得
x32=−2
;
3⋅x13+2⋅x23+1⋅x33=1
,但
x13=0,x23=0
,得
x33=1
。
第四行:
4⋅x11+3⋅x21+2⋅x31+1⋅x41=0
,即
4⋅1+3⋅(−2)+2⋅1+x41=0
,得
x41=0
;
4⋅x12+3⋅x22+2⋅x32+1⋅x42=0
,即
0+3⋅1+2⋅(−2)+x42=0
,得
x42=1
;
4⋅x13+3⋅x23+2⋅x33+1⋅x43=0
,即
0+0+2⋅1+x43=0
,得
x43=−2
;
4⋅x14+3⋅x24+2⋅x34+1⋅x44=1
,但
x14=0,x24=0,x34=0
,得
x44=1
。
因此,
D−1=1−21001−21001−20001, 即
A=1−21001−21001−20001. 18
求一个正交变换化二次型
f=x12+4x22+4x32−4x1x2+4x1x3−8x2x3
成标准形.
【答案】
二次型的标准形为
9y12
。
【解析】
二次型
f=x12+4x22+4x32−4x1x2+4x1x3−8x2x3
对应的矩阵为
求特征值:解特征方程
det(A−λI)=0
,即
det1−λ−22−24−λ−42−44−λ=0. 计算得
λ2(9−λ)=0
,特征值为
λ1=9
(单根),
λ2=0
(二重根)。
求特征向量:
- 对于
λ1=9
,解
(A−9I)v=0
,得特征向量
v1=1−22
,单位化得
q1=311−22
。
- 对于
λ2=0
,解
Av=0
,得特征向量
v2=210
,
v3=−201
。使用 Gram-Schmidt 正交化:
u2=v2=210
,
u3=v3−u2⋅u2v3⋅u2u2=−201−5−4210=−245
。
单位化:
q2=51210
,
q3=351−245
。
正交变换矩阵为
Q=31−323252510−352354355.
令
x=Qy
,则二次型化为标准形
f=9y12
。
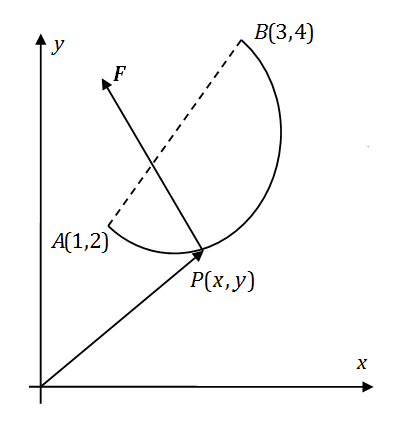
19
质点
P
沿着以
AB
为直径的圆周,从点
A(1,2)
运动到点
B(3,4)
的过程中受变力
F
作用(见图),
F
的大小等于点
P
与原点
O
之间的距离,其方向垂直于线段
OP
且与
y
轴正向的夹角小于
2π
.
求变力
F
对质点
P
所作的功.
【答案】
2(π−1)
【解析】
质点受变力
F
作用,力的大小等于点
P
与原点
O
之间的距离,即
∣F∣=x2+y2
,方向垂直于线段
OP
且与
y
轴正向的夹角小于
2π
。由此可得
F=(−y,x)
。
变力对质点所作的功为线积分
W=∫CF⋅dr=∫C(−ydx+xdy)
,其中路径
C
是以
AB
为直径的圆弧,从点
A(1,2)
到点
B(3,4)
。
圆的圆心为
AB
的中点
C(2,3)
,半径
r=2
。参数化路径:
x=2+2cosθ
,
y=3+2sinθ
,
其中
θ
从
−43π
到
4π
。
计算微分:
dx=−2sinθdθ
,
dy=2cosθdθ
。
代入积分:
W=∫−43π4π[−ydx+xdy]=∫−43π4π[−(3+2sinθ)(−2sinθdθ)+(2+2cosθ)(2cosθdθ)] 简化被积函数:
2[(3+2sinθ)sinθ+(2+2cosθ)cosθ]dθ=2[3sinθ+2sin2θ+2cosθ+2cos2θ]dθ =2[3sinθ+2cosθ+2(sin2θ+cos2θ)]dθ=2[3sinθ+2cosθ+2]dθ 因此,
W=2∫−43π4π[3sinθ+2cosθ+2]dθ 计算积分:
∫3sinθdθ=−3cosθ,∫2cosθdθ=2sinθ,∫2dθ=2θ 代入上下限:
[−3cosθ]−43π4π=−3[cos(4π)−cos(−43π)]=−3[22−(−22)]=−32 [2sinθ]−43π4π=2[sin(4π)−sin(−43π)]=2[22−(−22)]=22 [2θ]−43π4π=2[4π−(−43π)]=2π 积分结果为:
于是,
故变力
F
对质点
P
所作的功为
2(π−1)
。
填空题
20
已知随机变量
X
的概率密度函数
f(x)=21e−∣x∣
,
−∞<x<+∞
,
则
X
的概率分布函数
F(x)=
______.
【答案】
F(x)={21ex1−21e−xif x<0if x≥0
【解析】
概率分布函数
F(x)
定义为
F(x)=P(X≤x)=∫−∞xf(t)dt
。给定概率密度函数
f(x)=21e−∣x∣
,由于绝对值的存在,需分段计算。
当
x<0
时,在积分区间
(−∞,x]
上,有
∣t∣=−t
,所以:
F(x)=∫−∞x21e−∣t∣dt=∫−∞x21etdt=21[et]−∞x=21ex.
当
x≥0
时,积分需分成两段:
(−∞,0)
和
[0,x]
。在
(−∞,0)
上,有
∣t∣=−t
:
∫−∞021e−∣t∣dt=∫−∞021etdt=21[et]−∞0=21(1−0)=21.
在
[0,x]
上,有
∣t∣=t
:
∫0x21e−∣t∣dt=∫0x21e−tdt=21[−e−t]0x=21(1−e−x).
因此:
F(x)=21+21(1−e−x)=1−21e−x.
在
x=0
处,两种情况的取值均为
21
,故函数连续。
21
设随机事件
A
,
B
及其和事件
A∪B
的概率分别是
0.4
,
0.3
和
0.6
.
若
B
表示
B
的对立事件,那么积事件
AB
的概率
P(AB)=
______.
【答案】
0.3
【解析】
已知
P(A)=0.4
,
P(B)=0.3
,
P(A∪B)=0.6
。
根据概率的加法公式:
P(A∪B)=P(A)+P(B)−P(A∩B)
代入已知值:
0.6=0.4+0.3−P(A∩B)
解得:
P(A∩B)=0.4+0.3−0.6=0.1
事件
A
可以分解为互斥事件
A∩B
和
A∩B
的并集,因此:
P(A)=P(A∩B)+P(A∩B)
代入
P(A)=0.4
和
P(A∩B)=0.1
:
0.4=0.1+P(A∩B)
解得:
P(A∩B)=0.4−0.1=0.3
因此,积事件
AB
的概率为 0.3。
22
已知离散型随机变量
X
服从参数为
2
的泊松(Poisson)分布,即
P{X=k}=k!2ke−2
,
k=0,1,2,⋯
,则随机变量
Z=3X−2
的数学期望
E(Z)=
______.
【答案】
4
【解析】
已知随机变量
X
服从参数为
λ=2
的泊松分布,因此
E(X)=λ=2
。
对于随机变量
Z=3X−2
,根据数学期望的线性性质,有
E(Z)=E(3X−2)=3E(X)−2
。
代入
E(X)=2
,得
E(Z)=3×2−2=6−2=4
。
故随机变量
Z
的数学期望为 4。
23
设二维随机变量
(X,Y)
在区域
D:0<x<1,∣y∣<x
内服从均匀分布,
求关于
X
的边缘概率密度函数及随机变量
Z=2X+1
的方差
D(Z)
.
【答案】
关于
X
的边缘概率密度函数为
fX(x)=2x
(其中
0<x<1
),随机变量
Z=2X+1
的方差
D(Z)=92
。
【解析】
二维随机变量
(X,Y)
在区域
D:0<x<1,∣y∣<x
上服从均匀分布。区域
D
的面积为
A=∬Ddxdy=∫01∫−xxdydx=∫012xdx=[x2]01=1,
因此联合概率密度函数为
fX,Y(x,y)=1,(x,y)∈D.
关于
X
的边缘概率密度函数通过对
y
积分得到:
fX(x)=∫−∞∞fX,Y(x,y)dy=∫−xx1dy=2x,0<x<1.
对于随机变量
Z=2X+1
,其方差为
D(Z)=D(2X+1)=4D(X).
需要计算
D(X)=E[X2]−(E[X])2
。首先求
E[X]
:
E[X]=∫01x⋅2xdx=∫012x2dx=2[3x3]01=32.
然后求
E[X2]
:
E[X2]=∫01x2⋅2xdx=∫012x3dx=2[4x4]01=21.
因此
D(X)=21−(32)2=21−94=189−188=181.
最终
D(Z)=4×181=184=92.