卷 3 填空题 本题满分15分,每小题3分
1 设
y = ln ( 1 + 3 − x ) d y =
【答案】 d y = − 1 + 3 x ln 3 d x
【解析】 y = ln ( 1 + 3 − x ) d y
首先,求导数
d x d y u = 1 + 3 − x y = ln u
由链式法则,
d x d y = u 1 ⋅ d x d u .
计算
d x d u u = 1 + 3 − x 3 − x = e − x l n 3
d x d u = d x d ( 3 − x ) = d x d e − x l n 3 = e − x l n 3 ⋅ ( − ln 3 ) = − ln 3 ⋅ 3 − x .
代入得:
d x d y = 1 + 3 − x 1 ⋅ ( − ln 3 ⋅ 3 − x ) = − 1 + 3 − x ln 3 ⋅ 3 − x .
简化表达式:
1 + 3 − x 3 − x = 3 x 1 ⋅ 1 + 3 x 1 1 = 3 x 1 ⋅ 3 x 3 x + 1 1 = 3 x 1 ⋅ 3 x + 1 3 x = 3 x + 1 1 .
所以,
d x d y = − ln 3 ⋅ 1 + 3 x 1 .
因此,微分
d y = d x d y d x = − 1 + 3 x ln 3 d x .
2 曲线
y = e − x 2
【答案】 ( − 2 2 , 2 2 )
【解析】 y = e − x 2 y ′′ = e − x 2 ( 4 x 2 − 2 ) e − x 2 > 0 y ′′ 4 x 2 − 2 4 x 2 − 2 < 0 x 2 < 2 1 − 2 2 < x < 2 2 y ′′ < 0 ( − 2 2 , 2 2 )
3 ∫ 1 + ∞ x 2 l n x d x =
【答案】
【解析】 ∫ 1 + ∞ x 2 l n x d x u = ln x d v = x 2 1 d x d u = x 1 d x v = − x 1
∫ u d v = uv − ∫ v d u
得:
∫ 1 + ∞ x 2 ln x d x = [ − x ln x ] 1 + ∞ + ∫ 1 + ∞ x 2 1 d x
计算边界项:x → + ∞ x l n x → 0 − x l n x → 0 x = 1 ln 1 = 0 − 1 l n 1 = 0
∫ 1 + ∞ x 2 1 d x = [ − x 1 ] 1 + ∞ = b → + ∞ lim ( − b 1 ) − ( − 1 1 ) = 0 + 1 = 1
故原积分为 1。
4 质点以速度
t sin ( t 2 ) t 1 = 2 π t 2 = π
【答案】
2 1
【解析】
质点的速度函数为
v ( t ) = t sin ( t 2 ) t 1 = 2 π t 2 = π s = ∫ t 1 t 2 ∣ v ( t ) ∣ d t
由于
t [ t 1 , t 2 ] ∣ v ( t ) ∣ = ∣ t sin ( t 2 ) ∣ = t ∣ sin ( t 2 ) ∣
s = ∫ t 1 t 2 t ∣ sin ( t 2 ) ∣ d t
令
u = t 2 d u = 2 t d t t d t = 2 d u
当
t = t 1 u = ( 2 π ) 2 = 2 π 当
t = t 2 u = ( π ) 2 = π 代入得:
s = ∫ 2 π π ∣ sin u ∣ ⋅ 2 d u = 2 1 ∫ 2 π π ∣ sin u ∣ d u
在区间
[ 2 π , π ] sin u ≥ 0 ∣ sin u ∣ = sin u
s = 2 1 ∫ 2 π π sin u d u
计算积分:
∫ 2 π π sin u d u = [ − cos u ] 2 π π = − cos π − ( − cos 2 π ) = − ( − 1 ) − ( − 0 ) = 1
所以:
s = 2 1 × 1 = 2 1
因此,质点所经过的路程为
2 1
5 lim x → 0 + x + e x 1 1 − e x 1 =
【答案】
-1
【解析】
考虑极限
lim x → 0 + x + e x 1 1 − e x 1 x → 0 + e x 1 → + ∞ e x 1
x + e x 1 1 − e x 1 = x e − x 1 + 1 e − x 1 − 1 .
当
x → 0 + e − x 1 → 0 e − x 1 − 1 → − 1 x e − x 1 + 1 → 1 x e − x 1 → 0 − 1
或者,令
t = x 1 x → 0 + t → + ∞
t → + ∞ lim t 1 + e t 1 − e t = t → + ∞ lim 1 + t e t 1 e t 1 − 1 .
当
t → + ∞ e t 1 → 0 t e t 1 → 0 − 1 1 − 1
两种方法均得极限为
− 1
选择题 本题满分15分,每小题3分
6 若曲线
y = x 2 + a x + b 2 y = − 1 + x y 3 ( 1 , − 1 ) a b
查看答案与解析
正确答案:D 【解析】 ( 1 , − 1 )
首先,对于曲线
y = x 2 + a x + b ,
求导得
y ′ = 2 x + a .
在点
( 1 , − 1 )
2 ( 1 ) + a = 2 + a .
对于曲线
2 y = − 1 + x y 3 ,
使用隐函数求导,两边对
x 2 y ′ y 3 + 3 x y 2 y ′
2 y ′ = y 3 + 3 x y 2 y ′ .
代入点
( 1 , − 1 )
2 y ′ = ( − 1 ) 3 + 3 ( 1 ) ( − 1 ) 2 y ′ ,
即
2 y ′ = − 1 + 3 y ′ .
解得
y ′ = 1.
因此,第一条曲线在点
( 1 , − 1 ) 1
2 + a = 1 ,
解得
a = − 1.
又点
( 1 , − 1 )
− 1 = 1 2 + ( − 1 ) ( 1 ) + b ,
即
− 1 = 1 − 1 + b ,
解得
b = − 1.
故
a = − 1 , b = − 1
7 设函数
f ( x ) = { x 2 , 2 − x , 0 ≤ x ≤ 1 , 1 < x ≤ 2. F ( x ) = ∫ 0 x f ( t ) d t 0 ≤ x ≤ 2
查看答案与解析
正确答案:B 【解析】 f ( x ) F ( x ) = ∫ 0 x f ( t ) d t
因此,正确答案为 B 。
8 设函数
f ( x ) ( − ∞ , + ∞ ) x 0 = 0 f ( x )
查看答案与解析
正确答案:B 【解析】 设函数
f ( x ) ( − ∞ , + ∞ ) x 0 = 0 f ( x ) g ( x ) = − f ( − x ) g ( − x 0 ) = − f ( − ( − x 0 )) = − f ( x 0 ) x 0 f ( x ) x x 0 f ( x ) ≤ f ( x 0 ) g ( x ) y = − x 0 x y − x x 0 f ( − x ) ≤ f ( x 0 ) g ( x ) = − f ( − x ) ≥ − f ( x 0 ) = g ( y ) g ( x ) y = − x 0 − x 0 − f ( − x )
选项A错误,因为极大值点不一定可导,因此不一定是驻点。选项C错误,反例:设
f ( x ) = − ( x − 1 ) 2 x 0 = 1 − x 0 = − 1 − f ( x ) = ( x − 1 ) 2 x f ( x ) ≤ f ( x 0 )
因此,正确选项为B。
9 同试卷 1 第 6 题
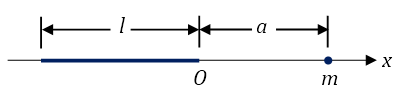
10 如图,
x μ l m a k
查看答案与解析
正确答案:A 【解析】 x = − l x = 0 x = a x μ d x a − x ( a − x ) 2 km μ d x x = − l x = 0
∫ − l 0 ( a − x ) 2 km μ d x .
故正确答案为 A 。
计算题 本题满分25分,每小题5分
11 设
{ x = t cos t y = t sin t d x 2 d 2 y
【答案】
d x 2 d 2 y = ( cos t − t sin t ) 3 t 2 + 2
【解析】
给定参数方程:
x = t cos t , y = t sin t
先求一阶导数
d x d y d t d x d t d y
d t d x = cos t − t sin t , d t d y = t cos t + sin t
则一阶导数为:
d x d y = d t d x d t d y = cos t − t sin t t cos t + sin t
再求二阶导数
d x 2 d 2 y
d x 2 d 2 y = d t d ( d x d y ) ⋅ d t d x 1
令
u = d x d y = g ( t ) f ( t ) f ( t ) = t cos t + sin t g ( t ) = cos t − t sin t d t d u
d t d u = [ g ( t ) ] 2 f ′ ( t ) g ( t ) − f ( t ) g ′ ( t )
计算
f ′ ( t ) g ′ ( t )
f ′ ( t ) = − t sin t + 2 cos t , g ′ ( t ) = − t cos t − 2 sin t
代入计算:
f ′ ( t ) g ( t ) = ( − t sin t + 2 cos t ) ( cos t − t sin t ) = t 2 sin 2 t + 2 cos 2 t − 3 t sin t cos t
f ( t ) g ′ ( t ) = ( t cos t + sin t ) ( − t cos t − 2 sin t ) = − t 2 cos 2 t − 3 t sin t cos t − 2 sin 2 t
则:
f ′ ( t ) g ( t ) − f ( t ) g ′ ( t ) = t 2 sin 2 t + 2 cos 2 t − 3 t sin t cos t + t 2 cos 2 t + 3 t sin t cos t + 2 sin 2 t = t 2 + 2
所以:
d t d u = ( cos t − t sin t ) 2 t 2 + 2
最后:
d x 2 d 2 y = d t d x d t d u = ( cos t − t sin t ) 2 t 2 + 2 ⋅ cos t − t sin t 1 = ( cos t − t sin t ) 3 t 2 + 2
12 计算
∫ 1 4 x ( 1 + x ) d x
【答案】
2 ln 3 4
【解析】
计算积分
∫ 1 4 x ( 1 + x ) d x u = x x = u 2 d x = 2 u d u x = 1 u = 1 x = 4 u = 2
∫ 1 4 x ( 1 + x ) d x = ∫ 1 2 u 2 ( 1 + u ) 2 u d u = ∫ 1 2 u ( 1 + u ) 2 d u . 将
u ( 1 + u ) 2
u ( 1 + u ) 2 = u 2 − 1 + u 2 .
代入积分:
∫ 1 2 ( u 2 − 1 + u 2 ) d u = 2 ∫ 1 2 u 1 d u − 2 ∫ 1 2 1 + u 1 d u = 2 [ ln u ] 1 2 − 2 [ ln ( 1 + u ) ] 1 2 .
计算定积分:
2 ( ln 2 − ln 1 ) − 2 ( ln 3 − ln 2 ) = 2 ln 2 − 0 − 2 ln 3 + 2 ln 2 = 4 ln 2 − 2 ln 3 = 2 ln ( 3 4 ) .
因此,积分结果为
2 ln 3 4
13 求
lim x → 0 x 2 ( e x − 1 ) x − s i n x
【答案】
6 1
【解析】
考虑极限
lim x → 0 x 2 ( e x − 1 ) x − s i n x x → 0 x − sin x → 0 x 2 ( e x − 1 ) → 0 0 0
分子
x − sin x x − ( x − 6 x 3 + 120 x 5 − ⋯ ) = 6 x 3 − 120 x 5 + ⋯
分母
x 2 ( e x − 1 ) x 2 ( x + 2 x 2 + 6 x 3 + ⋯ ) = x 3 + 2 x 4 + 6 x 5 + ⋯
因此,原式化为:
x 3 + 2 x 4 + 6 x 5 + ⋯ 6 x 3 − 120 x 5 + ⋯ = 1 + 2 x + 6 x 2 + ⋯ 6 1 − 120 x 2 + ⋯
当
x → 0 6 1 6 1
Alternatively, 使用洛必达法则验证。第一次应用洛必达法则:
x → 0 lim 2 x ( e x − 1 ) + x 2 e x 1 − cos x
仍为
0 0
x → 0 lim 2 ( e x − 1 ) + 4 x e x + x 2 e x sin x
分子
sin x ∼ x 2 ( e x − 1 ) + 4 x e x + x 2 e x ∼ 2 x + 4 x = 6 x 6 x x = 6 1
14 求
∫ x sin 2 x d x
【答案】
4 x 2 − 4 x sin 2 x − 8 cos 2 x + C
【解析】
首先,利用三角恒等式
sin 2 x = 2 1 − c o s 2 x
∫ x sin 2 x d x = ∫ x ⋅ 2 1 − cos 2 x d x = 2 1 ∫ x d x − 2 1 ∫ x cos 2 x d x
计算第一个积分:
∫ x d x = 2 x 2 ∫ x cos 2 x d x u = x d v = cos 2 x d x d u = d x v = 2 s i n 2 x
∫ x cos 2 x d x = x ⋅ 2 sin 2 x − ∫ 2 sin 2 x d x = 2 x sin 2 x − 2 1 ∫ sin 2 x d x
其中
∫ sin 2 x d x = − 2 c o s 2 x
∫ x cos 2 x d x = 2 x sin 2 x + 4 cos 2 x
代入原积分:
∫ x sin 2 x d x = 2 1 ⋅ 2 x 2 − 2 1 ( 2 x sin 2 x + 4 cos 2 x ) + C = 4 x 2 − 4 x sin 2 x − 8 cos 2 x + C
这就是最终结果。
15 求微分方程
x y ′ + y = x e x y ( 1 ) = 1
【答案】
y = x e x ( x − 1 ) + 1
【解析】
给定微分方程
x y ′ + y = x e x y ( 1 ) = 1
首先将方程化为标准形式
y ′ + x 1 y = e x .
积分因子为
μ ( x ) = e ∫ x 1 d x = x .
乘以积分因子后,方程变为
( x y ) ′ = x e x .
两边积分得
x y = ∫ x e x d x .
计算积分
∫ x e x d x = x e x − e x + C ,
所以
x y = x e x − e x + C ,
即
y = e x − x e x + x C .
代入初始条件
y ( 1 ) = 1
1 = e 1 − 1 e 1 + 1 C = C ,
所以
C = 1
因此特解为
y = e x − x e x + x 1 = x e x ( x − 1 ) + 1 .
解答题 16 利用导数证明:当
x > 1 l n x l n ( 1 + x ) > 1 + x x
【答案】
【解析】 g ( x ) = ( 1 + x ) ln ( 1 + x ) − x ln x x > 1 l n x l n ( 1 + x ) > 1 + x x g ( x ) > 0 g ′ ( x ) = ln ( 1 + x ) − ln x = ln ( 1 + x 1 ) x > 1 1 + x 1 > 1 ln ( 1 + x 1 ) > 0 g ′ ( x ) > 0 g ( x ) x > 1 g ( 1 ) = 2 ln 2 > 0 x > 1 g ( x ) > 0
17 求微分方程
y ′′ + y = x + cos x
【答案】
y = C 1 cos x + C 2 sin x + x + 2 1 x sin x
其中
C 1 C 2
【解析】
微分方程
y ′′ + y = x + cos x
齐次方程
y ′′ + y = 0 r 2 + 1 = 0 r = ± i
y h = C 1 cos x + C 2 sin x
非齐次项
x + cos x x cos x
对于
x y p 1 = A x + B y ′′ + y = 0 + ( A x + B ) = x A = 1 B = 0 y p 1 = x 对于
cos x cos x y p 2 = x ( C cos x + D sin x ) y ′′ + y = 2 D cos x − 2 C sin x = cos x D = 2 1 C = 0 y p 2 = 2 1 x sin x 特解为
y p = y p 1 + y p 2 = x + 2 1 x sin x
y = y h + y p = C 1 cos x + C 2 sin x + x + 2 1 x sin x
18 曲线
y = ( x − 1 ) ( x − 2 ) x y
【答案】
2 π
【解析】
曲线
y = ( x − 1 ) ( x − 2 ) x x = 1 x = 2 x y V = 2 π ∫ a b x ∣ y ∣ d x [ 1 , 2 ] y ≤ 0 ∣ y ∣ = − y
V = 2 π ∫ 1 2 x [ − ( x − 1 ) ( x − 2 ) ] d x = 2 π ∫ 1 2 x ( − x 2 + 3 x − 2 ) d x = 2 π ∫ 1 2 ( − x 3 + 3 x 2 − 2 x ) d x .
计算积分:
∫ ( − x 3 + 3 x 2 − 2 x ) d x = − 4 x 4 + x 3 − x 2 ,
代入上下限:
[ − 4 x 4 + x 3 − x 2 ] 1 2 = ( − 4 16 + 8 − 4 ) − ( − 4 1 + 1 − 1 ) = ( − 4 + 8 − 4 ) − ( − 4 1 ) = 0 + 4 1 = 4 1 .
所以,
V = 2 π × 4 1 = 2 π .
也可用圆盘法验证:解出
x = 2 3 ± 1 + 4 y y ∈ [ − 0.25 , 0 ] π ( x r 2 − x l 2 ) = 3 1 + 4 y
V = π ∫ − 0.25 0 3 1 + 4 y d y = 3 π ∫ 0 1 4 u 1/2 d u = 4 3 π ⋅ 3 2 = 2 π , 结果一致。
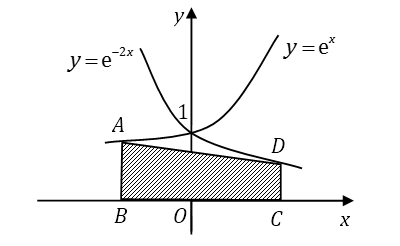
19 如图,
A D y = e x y = e − 2 x A B D C x ∣ A B ∣ : ∣ D C ∣ = 2 : 1 ∣ A B ∣ < 1 B C A BC D
【答案】 B 3 1 ln 2 − 1 C 2 1 + 3 1 ln 2
【解析】 B b C c A B D C x A y = e x D y = e − 2 x ∣ A B ∣ = e b ∣ D C ∣ = e − 2 c ∣ A B ∣ : ∣ D C ∣ = 2 : 1 e b / e − 2 c = 2 e b + 2 c = 2 b + 2 c = ln 2 A BC D S
S = 2 1 ( ∣ A B ∣ + ∣ D C ∣ ) ⋅ ( c − b ) = 2 1 ( e b + e − 2 c ) ( c − b )
利用约束
b = ln 2 − 2 c
S = 2 1 ( e l n 2 − 2 c + e − 2 c ) ( c − ( ln 2 − 2 c ) ) = 2 1 ( 2 e − 2 c + e − 2 c ) ( 3 c − ln 2 ) = 2 1 ⋅ 3 e − 2 c ( 3 c − ln 2 ) = 2 3 e − 2 c ( 3 c − ln 2 )
令
S ( c ) = 2 3 e − 2 c ( 3 c − ln 2 )
S ′ ( c ) = 2 3 [ e − 2 c ⋅ 3 + ( 3 c − ln 2 ) ⋅ ( − 2 ) e − 2 c ] = 2 3 e − 2 c ( 3 − 6 c + 2 ln 2 )
设
S ′ ( c ) = 0 3 − 6 c + 2 ln 2 = 0 c = 2 1 + 3 l n 2 b = ln 2 − 2 c b = ln 2 − 2 ( 2 1 + 3 l n 2 ) = 3 1 ln 2 − 1 ∣ A B ∣ = e b = e 3 1 l n 2 − 1 = 2 1/3 / e < 1 B 3 1 ln 2 − 1 C 2 1 + 3 1 ln 2 A BC D
20 设函数
f ( x ) ( − ∞ , + ∞ ) f ( x ) = f ( x − π ) + sin x f ( x ) = x x ∈ [ 0 , π ) ∫ π 3 π f ( x ) d x
【答案】
π 2 − 2
【解析】
由题设,函数
f ( x ) f ( x ) = f ( x − π ) + sin x x ∈ [ 0 , π ) f ( x ) = x ∫ π 3 π f ( x ) d x
首先,求
f ( x ) [ π , 3 π ]
当
x ∈ [ π , 2 π ) x − π ∈ [ 0 , π ) f ( x − π ) = x − π f ( x ) = f ( x − π ) + sin x = ( x − π ) + sin x 当
x ∈ [ 2 π , 3 π ] x − π ∈ [ π , 2 π ) f ( x − π ) = ( x − π − π ) + sin ( x − π ) = ( x − 2 π ) − sin x sin ( x − π ) = − sin x f ( x ) = f ( x − π ) + sin x = ( x − 2 π ) − sin x + sin x = x − 2 π 因此,积分可拆分为两部分:
∫ π 3 π f ( x ) d x = ∫ π 2 π f ( x ) d x + ∫ 2 π 3 π f ( x ) d x
其中:
∫ π 2 π f ( x ) d x = ∫ π 2 π [( x − π ) + sin x ] d x ∫ π 2 π ( x − π ) d x = [ 2 1 ( x − π ) 2 ] π 2 π = 2 1 π 2 − 0 = 2 π 2 ∫ π 2 π sin x d x = [ − cos x ] π 2 π = ( − cos 2 π ) − ( − cos π ) = ( − 1 ) − ( 1 ) = − 2 所以
∫ π 2 π f ( x ) d x = 2 π 2 − 2 ∫ 2 π 3 π f ( x ) d x = ∫ 2 π 3 π ( x − 2 π ) d x 令
u = x − 2 π x = 2 π u = 0 x = 3 π u = π ∫ 0 π u d u = [ 2 1 u 2 ] 0 π = 2 1 π 2 因此,
∫ π 3 π f ( x ) d x = ( 2 π 2 − 2 ) + 2 π 2 = π 2 − 2