卷 3
填空题
本题共5小题,每小题3分,满分15分
1
若
f(x)={xsin2x+e2ax−1,a,x=0,x=0
在
(−∞,+∞)
上连续,则
a=
______.
【答案】
-2
【解析】
函数
f(x)
在
x=0
处连续,因此需满足:
x→0limf(x)=f(0)=a
即计算极限:
x→0limxsin2x+e2ax−1
当
x→0
时,该极限为
00
型不定式。使用等价无穷小替换:
sin2x∼2x
,
e2ax−1∼2ax
,代入得:
x→0limx2x+2ax=x→0limx2x(1+a)=2(1+a)
令极限等于
a
:
2(1+a)=a
解得:
2+2a=a⟹a=−2
因此,
a=−2
。
2
设函数
y=y(x)
由参数方程
{x=t−ln(1+t),y=t3+t2
所确定,则
dx2d2y=
______.
【答案】
t(6t+5)(1+t)
或等价形式如
t6t2+11t+5
或
6t+11+t5
【解析】
给定参数方程:
x=t−ln(1+t),y=t3+t2
首先求一阶导数
dxdy
。
计算
dtdx
和
dtdy
:
dtdx=dtd[t−ln(1+t)]=1−1+t1=1+tt
dtdy=dtd[t3+t2]=3t2+2t
则一阶导数为:
dxdy=dx/dtdy/dt=1+tt3t2+2t=(3t2+2t)⋅t1+t=(3t+2)(1+t)=3t2+5t+2
接下来求二阶导数
dx2d2y
:
dx2d2y=dxd(dxdy)=dtdxdtd(dxdy)
其中:
dtd(dxdy)=dtd(3t2+5t+2)=6t+5
代入得:
dx2d2y=1+tt6t+5=(6t+5)⋅t1+t=t(6t+5)(1+t)
该结果可简化为
t6t2+11t+5
或
6t+11+t5
。
3
dxd[∫0cos3xf(t)dt]=
______.
【答案】
−3sin3x⋅f(cos3x)
【解析】
设
u=cos3x
,则原函数为
G(x)=∫0uf(t)dt.
根据微积分基本定理,
dudG=f(u)=f(cos3x).
同时,
dxdu=dxd(cos3x)=−3sin3x.
由链式法则,
dxdG=dudG⋅dxdu=f(cos3x)⋅(−3sin3x)=−3sin3x⋅f(cos3x).
因此,导数为
−3sin3x⋅f(cos3x).
4
∫x3ex2dx=
______.
【答案】
21ex2(x2−1)+C
【解析】
考虑积分
∫x3ex2dx
。令
u=x2
,则
du=2xdx
,即
xdx=2du
。将积分改写为:
∫x3ex2dx=∫x2⋅x⋅ex2dx=∫ueu⋅2du=21∫ueudu.
现在计算
∫ueudu
,使用分部积分法。设
v=u
,
dw=eudu
,则
dv=du
,
w=eu
。代入分部积分公式:
∫ueudu=ueu−∫eudu=ueu−eu+C=eu(u−1)+C.
代回
u=x2
,得到:
21∫ueudu=21ex2(x2−1)+C.
因此,积分结果为
21ex2(x2−1)+C
。验证求导:对
21ex2(x2−1)
求导,得到
x3ex2
,符合原被积函数。
5
微分方程
ydx+(x2−4x)dy=0
的通解为 ______.
【答案】
y4=Cx−4x
,其中
C
为任意常数。
【解析】
给定微分方程
ydx+(x2−4x)dy=0
,首先改写为
dxdy=−x2−4xy
因式分解分母
x2−4x=x(x−4)
,得
dxdy=−x(x−4)y
分离变量:
ydy=−x(x−4)dx
对右边分式进行部分分式分解:
x(x−4)1=xA+x−4B
解得
A=−41
,
B=41
,所以
−x(x−4)1=41(x1−x−41)
代入方程:
ydy=41(x1−x−41)dx
积分两边:
∫ydy=41∫(x1−x−41)dx
ln∣y∣=41(ln∣x∣−ln∣x−4∣)+C1
令
C=e4C1
,则
因此通解为
y4=Cx−4x
其中
C
为任意常数。当
C=0
时,对应解
y=0
。
选择题
本题共5小题,每小题3分,满分15分
6
设
limx→0x2ln(1+x)−(ax+bx2)=2
,则
正确答案:A【解析】
给定极限
x→0limx2ln(1+x)−(ax+bx2)=2,
首先将
ln(1+x)
展开为泰勒级数:
ln(1+x)=x−2x2+3x3−⋯.
代入分子得
ln(1+x)−ax−bx2=(1−a)x+(−21−b)x2+3x3−⋯.
除以
x2
后为
x1−a+(−21−b)+3x−⋯.
为使极限存在,必须使
x1−a
的系数为零,即
1−a=0,
解得
a=1
。
代入
a=1
,表达式变为
x2ln(1+x)−x−bx2=−(21+b)+3x−⋯.
取极限得
−(21+b)=2,
解得
b=−25.
因此
a=1, b=−25
,对应选项 A。
7
设
f(x)={32x3,x2,x≤1,x>1,
则
f(x)
在
x=1
处
正确答案:B【解析】
函数
f(x)
在
x=1
处定义为
f(1)=32×13=32.
左导数定义为
f−′(1)=h→0−limhf(1+h)−f(1).
当
h→0−
时,
1+h<1
,故
f(1+h)=32(1+h)3.
计算得:
f−′(1)=h→0−limh32(1+h)3−32=h→0−lim32⋅h(1+h)3−1=h→0−lim32⋅h3h+3h2+h3=h→0−lim32(3+3h+h2)=32×3=2.
左导数存在且为
2
。
右导数定义为
f+′(1)=h→0+limhf(1+h)−f(1).
当
h→0+
时,
1+h>1
,故
f(1+h)=(1+h)2.
计算得:
f+′(1)=h→0+limh(1+h)2−32=h→0+limh1+2h+h2−32=h→0+limh31+2h+h2=h→0+lim(3h1+2+h).
当
h→0+
时,
3h1→+∞
,故极限不存在。因此右导数不存在。
综上,左导数存在,右导数不存在,对应选项 B。
8
设
y=f(x)
是满足微分方程
y′′+y′−esinx=0
的解,且
f′(x0)=0
,则
f(x)
在
正确答案:C【解析】
由微分方程
y′′+y′−esinx=0
可得
y′′=esinx−y′.
在点
x0
处,已知
f′(x0)=0
,代入得
f′′(x0)=esinx0−f′(x0)=esinx0.
由于
esinx0>0
恒成立,因此
f′′(x0)>0
。
结合
f′(x0)=0
,根据极值的二阶导数判别法,函数
f(x)
在
x0
处取得极小值。
选项 A 和 B 涉及邻域内的单调性,但由于在
x0
处取得极小值,邻域内的单调性可能变化,故不选 A 或 B。
选项 D 表示极大值,与结论不符。
因此正确选项为 C。
9
曲线
y=ex21arctan(x+1)(x−2)x2+x+1
的渐近线有
正确答案:B【解析】
首先,考虑水平渐近线。
当
x→∞
或
x→−∞
时,
ex21→1,
且
(x+1)(x−2)x2+x+1→1,
因此
arctan(x+1)(x−2)x2+x+1→arctan1=4π.
故
y→4π
,存在水平渐近线
y=4π.
其次,考虑垂直渐近线。
函数在
x=−1
、
x=0
、
x=2
处未定义。
在
x=−1
和
x=2
处,极限为有限值,无垂直渐近线。
在
x=0
处,
ex21→∞,
且
arctan(x+1)(x−2)x2+x+1→arctan(−21)
为有限值,故
y→∞
(具体为
−∞
),存在垂直渐近线
x=0.
最后,考虑斜渐近线。
由于存在水平渐近线,当
x→±∞
时无斜渐近线。
因此,渐近线共有 2 条。
10
同试卷 1 第 6 题
解答题
本题共5小题,每小题5分,满分25分
11
设
y=f(x+y)
,其中
f
具有二阶导数,且其一阶导数不等于
1
,求
dx2d2y
.
【答案】
dx2d2y=[1−f′(x+y)]3f′′(x+y)
【解析】
给定
y=f(x+y)
,其中
f
具有二阶导数,且
f′=1
。设
u=x+y
,则
y=f(u)
。对两边关于
x
求一阶导数:
dxdy=f′(u)⋅dxdu=f′(u)⋅(1+dxdy)
解得:
dxdy=1−f′(u)f′(u)
再对两边关于
x
求二阶导数:
dx2d2y=dxd(1−f′(u)f′(u))
使用链式法则和商法则,令
v=f′(u)
,则:
dxd(1−vv)=(1−v)2v′
其中
v′=dxdv=f′′(u)⋅dxdu=f′′(u)⋅(1+dxdy)
。代入一阶导数结果:
1+dxdy=1+1−f′(u)f′(u)=1−f′(u)1
所以:
v′=f′′(u)⋅1−f′(u)1
代入二阶导数:
dx2d2y=[1−f′(u)]2f′′(u)⋅1−f′(u)1=[1−f′(u)]3f′′(u)
将
u=x+y
代回,得:
dx2d2y=[1−f′(x+y)]3f′′(x+y)
12
计算
∫01x(1−x4)23dx
.
【答案】
323π
【解析】
计算积分
∫01x(1−x4)23dx
令
x2=sinθ
,则
2xdx=cosθdθ
即
xdx=21cosθdθ
当
x=0
时,
θ=0
;当
x=1
时,
θ=2π
。
代入积分得:
∫01x(1−x4)23dx=∫02π21cosθ⋅(1−sin2θ)23dθ=21∫02πcosθ⋅cos3θdθ=21∫02πcos4θdθ
计算
∫02πcos4θdθ
。利用倍角公式:
cos4θ=(21+cos2θ)2=41(1+2cos2θ+cos22θ)=41(1+2cos2θ+21+cos4θ)=83+21cos2θ+81cos4θ
积分得:
∫02πcos4θdθ=∫02π(83+21cos2θ+81cos4θ)dθ=[83θ+41sin2θ+321sin4θ]02π=83⋅2π=163π
因此,
21∫02πcos4θdθ=21⋅163π=323π
故积分值为
323π
。
13
计算
limn→∞tann(4π+n2)
.
【答案】
e4
【解析】
考虑极限
n→∞limtann(4π+n2)
令
t=tan(n2)
则
tan(4π+n2)=1−t1+t
当
n→∞
时,
n2→0
,故
t≈n2
因此,原极限化为
n→∞lim(1−n21+n2)n
令
y=(1−n21+n2)n
取自然对数:
lny=nln(1−n21+n2)=n[ln(1+n2)−ln(1−n2)]
利用泰勒展开:
ln(1+x)≈x−2x2+3x3−⋯
ln(1−x)≈−x−2x2−3x3−⋯
代入
x=n2
,得:
ln(1−n21+n2)≈n4+O(n31)
故
lny≈n⋅n4=4
因此
y→e4
即使考虑
tan(n2)
的高阶项,极限仍为
e4
。
所以,原极限为
e4
14
同试卷 1 第 13 题
15
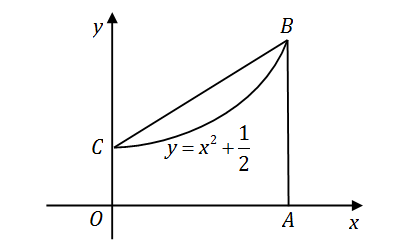
如图,设曲线方程为
y=x2+21
,梯形
OABC
的面积为
D
,
曲边梯形
OABC
的面积为
D1
,点
A
的坐标为
(a,0)
(
a>0
).证明:
D1D<23
.
【解析】
设点
O(0,0)
,
A(a,0)
(
a>0
),
B(a,a2+21)
,
C(0,21)
。梯形
OABC
的平行边为
OC
和
AB
,长度分别为
21
和
a2+21
,高为
a
,其面积为:
D=21(21+a2+21)a=2a(a2+1).
曲边梯形
OABC
为由曲线
y=x2+21
、直线
x=a
、x 轴和 y 轴围成的区域,其面积为:
D1=∫0a(x2+21)dx=[31x3+21x]0a=31a3+21a.
计算比值:
D1D=31a3+21a2a(a2+1)=21a(32a2+1)21a(a2+1)=32a2+1a2+1=2a2+33(a2+1).
需证
2a2+33(a2+1)<23
。由于
a>0
,分母
2a2+3>0
,不等式等价于:
2a2+3a2+1<21.
交叉相乘得:
2(a2+1)<2a2+3,
即
2a2+2<2a2+3
,化简得
2<3
,恒成立。因此,
D1D<23
得证。
解答题
16
设当
x>0
时,方程
kx+x21=1
有且仅有一个解,求
k
的取值范围.
【答案】
【解析】
考虑函数
f(x)=kx+x21−1
,其中
x>0
。
方程
kx+x21=1
有且仅有一个解,等价于
f(x)
在
x>0
时只有一个零点。
1. 当
k≤0
时
导数
f′(x)=k−x32<0(对所有 x>0),
因此
f(x)
严格递减。
当
x→0+
时,
x21→+∞
,故
f(x)→+∞
;
当
x→+∞
时:
- 若
k<0
,则
f(x)→−∞
;
- 若
k=0
,则
f(x)→−1
。
由于
f(x)
严格递减且从正无穷开始,必存在唯一的
x>0
使
f(x)=0
。
因此,对
k≤0
,方程有且仅有一个解。
2. 当
k>0
时
此时
f(x)
不是单调的。计算导数
f′(x)=k−x32.
令
f′(x)=0
,得临界点
x0=(k2)1/3.
当
x<x0
时,
f′(x)<0
;当
x>x0
时,
f′(x)>0
,
所以
x0
是极小值点。
极小值为
f(x0)=kx0+x021−1=22/33k2/3−1.
方程有解的条件是
f(x0)≤0
,即
22/33k2/3≤1.
- 若
22/33k2/3<1
,即
k<332
,则
f(x0)<0
,方程有两个解;
- 若
22/33k2/3>1
,即
k>332
,则
f(x0)>0
,方程无解;
- 若
22/33k2/3=1
,即
k=332=923
,则
f(x0)=0
,方程有且仅有一个解(位于
x=x0
处)。
综上,方程有且仅有一个解时,
k
的取值范围为
17
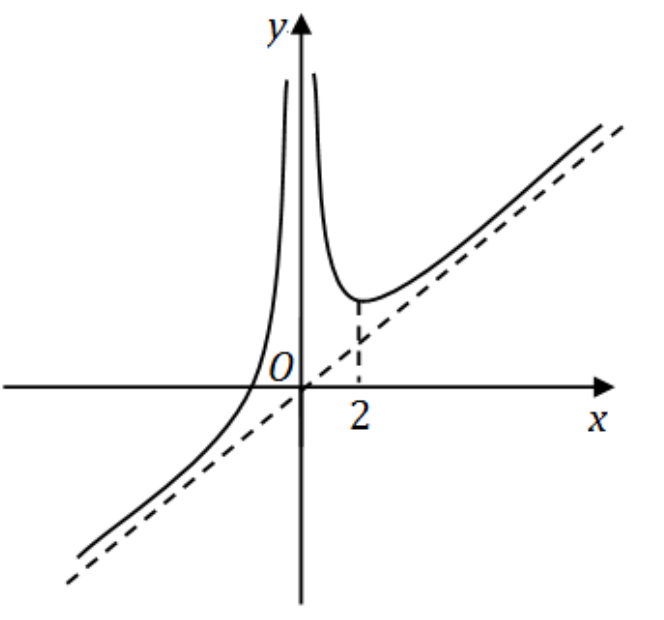
设
y=x2x3+4
,
(1) 求函数的增减区间及极值;
(2) 求函数图像的凹凸区间及拐点;
(3) 求其渐近线;
(4) 作出其图形.
【答案】
(1) 函数在
(−∞,0)
和
(2,+∞)
上单调递增,在
(0,2)
上单调递减;极小值点为
(2,3)
,无极大值点。
(2) 函数在
(−∞,0)
和
(0,+∞)
上均为凹向上;无拐点。
(3) 渐近线:垂直渐近线
x=0
,斜渐近线
y=x
。
(4) 图形基于以上性质绘制:函数图像在
x=0
处有垂直渐近线,以
y=x
为斜渐近线,在
x=2
处取得极小值点
(2,3)
,在
(−∞,0)
上递增且凹向上,在
(0,2)
上递减且凹向上,在
(2,+∞)
上递增且凹向上。
【解析】
函数
y=x2x3+4=x+x24
。
(1) 求一阶导数
y′=1−x38
。令
y′=0
,得
x=2
。分析符号:当
x<0
时,
y′>0
;当
0<x<2
时,
y′<0
;当
x>2
时,
y′>0
。因此,函数在
(−∞,0)
和
(2,+∞)
上递增,在
(0,2)
上递减。极小值点为
(2,3)
。
(2) 求二阶导数
y′′=x424
。由于
y′′>0
对于所有
x=0
,函数在
(−∞,0)
和
(0,+∞)
上凹向上,无拐点。
(3) 渐近线:当
x→0
时,
y→∞
,故
x=0
为垂直渐近线。当
x→±∞
时,计算
m=limx→±∞xy=1
,
b=limx→±∞(y−mx)=0
,故
y=x
为斜渐近线。
(4) 图形基于上述分析绘制:定义域
x=0
,函数在
x=0
处趋于无穷,在
x=2
处取极小值,且始终在渐近线
y=x
上方。
18
求微分方程
y′′+a2y=sinx
的通解,其中常数
a>0.
【答案】
当
a=1
时,通解为
y=C1cos(ax)+C2sin(ax)+a2−1sinx
;
当
a=1
时,通解为
y=C1cosx+C2sinx−21xcosx
,
其中
C1
和
C2
为任意常数。
【解析】
给定微分方程
y′′+a2y=sinx
是一个二阶线性非齐次微分方程。通解由齐次方程的通解和非齐次方程的特解组成。
首先,求齐次方程
y′′+a2y=0
的通解。
特征方程为
r2+a2=0
,解得
r=±ai
,因此齐次通解为
yh=C1cos(ax)+C2sin(ax)
其次,求非齐次方程的特解
yp
。根据非齐次项
sinx
的形式,需分两种情况:
最终,通解为齐次通解与特解之和。
19
设
f(x)
在
[0,1]
上连续且递减,证明:当
0<λ<1
时,
∫0λf(x)dx≥λ∫01f(x)dx
.
【解析】
考虑函数
g(λ)=∫0λf(x)dx−λ∫01f(x)dx
。需要证明当
0<λ<1
时,有
g(λ)≥0
。
首先,计算
g(0)
和
g(1)
:
因此,
g(0)=0
和
g(1)=0
。
接下来,计算
g(λ)
的导数。由微积分基本定理,有
g′(λ)=dλd∫0λf(x)dx−∫01f(x)dx=f(λ)−∫01f(x)dx
令
C=∫01f(x)dx
,则
g′(λ)=f(λ)−C
。
由于
f(x)
在
[0,1]
上连续且递减,因此
f(λ)
随
λ
增加而减小,故
g′(λ)
也是递减函数。
当
λ=0
时,
g′(0)=f(0)−C
。
因为
f(x)
递减,有
f(x)≤f(0)
对于所有
x∈[0,1]
,所以
C=∫01f(x)dx≤f(0)⋅1=f(0)
即
g′(0)≥0
。
当
λ=1
时,
g′(1)=f(1)−C
。
因为
f(x)≥f(1)
对于所有
x∈[0,1]
,所以
C≥f(1)⋅1=f(1)
即
g′(1)≤0
。
因此,
g′(λ)
从
g′(0)≥0
开始,递减至
g′(1)≤0
,故存在点
λ0∈(0,1)
使得
g′(λ0)=0
,且当
λ<λ0
时
g′(λ)>0
,当
λ>λ0
时
g′(λ)<0
。这意味着
g(λ)
在
[0,λ0]
上单调递增,在
[λ0,1]
上单调递减。
由于
g(0)=0
和
g(1)=0
,且
g(λ)
先增后减,因此对于所有
λ∈(0,1)
,有
g(λ)≥0
,即
∫0λf(x)dx≥λ∫01f(x)dx
不等式得证。
20
求曲线
y=3−∣x2−1∣
与
x
轴围成的封闭图形绕直线
y=3
旋转所得的旋转体体积.
【答案】
15448π
【解析】
曲线
y=3−∣x2−1∣
与
x
轴围成的封闭图形位于
x
轴上方,且与
x
轴的交点为
x=±2
。该图形绕直线
y=3
旋转时,旋转体体积可通过固定
x
处的截面面积积分求解。
对于固定
x
,截面为圆环,外半径为
3−0=3
,内半径为
3−f(x)
,其中
f(x)=3−∣x2−1∣
。截面面积
A(x)=π[32−(3−f(x))2]=π[9−(9−6f(x)+f(x)2)]=π(6f(x)−f(x)2)
。
体积
V=∫−22A(x)dx=π∫−22[6f(x)−f(x)2]dx
。由于
f(x)
为偶函数,可计算从
0
到
2
的积分后乘以
2
,即
V=2π∫02[6f(x)−f(x)2]dx
.
函数
f(x)
在
[0,2]
上分段:
- 当
x∈[0,1]
时,
f(x)=2+x2
;
- 当
x∈[1,2]
时,
f(x)=4−x2
.
计算积分:
I1=∫01[6(2+x2)−(2+x2)2]dx=∫01[8+2x2−x4]dx=[8x+32x3−51x5]01=8+32−51=15127.
I2=∫12[6(4−x2)−(4−x2)2]dx=∫12[8+2x2−x4]dx=[8x+32x3−51x5]12=(16+316−532)−(8+32−51)=15224−15127=1597.
于是,
∫02[6f(x)−f(x)2]dx=I1+I2=15127+1597=15224,
所以
V=2π×15224=15448π.