卷 3
填空题
本题共5小题,每小题3分,满分15分
1
设
y=(x+e−2x)32
,则
y′∣x=0=
______.
【答案】
31
【解析】
给定函数
y=(x+e−2x)32
,求
y′∣x=0
。
设
u=x+e−2x
,则
y=u32
。
应用链式法则:
dxdy=dudy⋅dxdu=32u−31⋅dxdu.
计算
dxdu
:
dxdu=dxd(x)+dxd(e−2x)=1+e−2x⋅(−21)=1−21e−2x.
因此,
y′=32(x+e−2x)−31⋅(1−21e−2x).
代入
x=0
:
u∣x=0=0+e0=1,
y′∣x=0=32⋅1−31⋅(1−21⋅1)=32⋅1⋅(1−21)=32⋅21=31.
故
y′∣x=0=31
。
2
∫−11(x+1−x2)2dx=
______.
【答案】
2
【解析】
首先,展开被积函数:
(x+1−x2)2=x2+2x1−x2+(1−x2)=1+2x1−x2 因此,积分变为:
∫−11(1+2x1−x2)dx=∫−111dx+2∫−11x1−x2dx 计算第一个积分:
计算第二个积分:
由于
x1−x2
是奇函数(因为
x
是奇函数,
1−x2
是偶函数,乘积为奇函数),且在对称区间
[−1,1]
上,奇函数的积分为零,因此:
所以,原积分为:
2+2×0=2
因此,答案为 2。
3
微分方程的
y′′+2y′+5y=0
通解为 ______.
【答案】
y=e−x(C1cos2x+C2sin2x)
,其中
C1
和
C2
为任意常数。
【解析】
给定微分方程
y′′+2y′+5y=0
,这是一个二阶常系数线性齐次微分方程。
假设解的形式为
y=erx
,代入方程得到特征方程
r2+2r+5=0
。
解特征方程:
r=2−2±4−20=2−2±−16=2−2±4i=−1±2i 特征根为共轭复数
r1=−1+2i
和
r2=−1−2i
,因此通解为
y=e−x(C1cos2x+C2sin2x)
其中
C1
和
C2
为任意常数。
4
x→∞limx[sinln(1+x3)−sinln(1+x1)]=
【答案】
2
【解析】
考虑极限
limx→∞x[sinln(1+x3)−sinln(1+x1)]
。令
t=x1
,则当
x→∞
时,
t→0+
,极限化为:
t→0+limtsinln(1+3t)−sinln(1+t)
该极限等价于函数
f(t)=sinln(1+3t)−sinln(1+t)
在
t=0
处的导数。计算
f′(t)
:
f′(t)=cosln(1+3t)⋅1+3t3−cosln(1+t)⋅1+t1
代入
t=0
:
f′(0)=cosln1⋅13−cosln1⋅11=cos0⋅3−cos0⋅1=1⋅3−1⋅1=2
因此,原极限为 2。
5
由曲线
y=x+x1
,
x=2
及
y=2
所围图形的面积
S=
______.
【答案】
ln2−21
【解析】
曲线
y=x+x1
与直线
y=2
相交时,解方程
x+x1=2
,得
x2−2x+1=0
,即
(x−1)2=0
,所以交点为
x=1
。
直线
x=2
与曲线相交于
y=2+21=25
,即点
(2,25)
。
直线
x=2
与
y=2
相交于点
(2,2)
。
因此,所围图形位于
x=1
到
x=2
之间,且曲线
y=x+x1
在
y=2
之上。
面积
S
为曲线与直线
y=2
之间的差在区间
[1,2]
上的积分:
S=∫12(x+x1−2)dx
计算积分:
∫(x+x1−2)dx=2x2+ln∣x∣−2x
代入上下限:
[2x2+lnx−2x]12=(24+ln2−4)−(21+ln1−2)=(2+ln2−4)−(0.5−2)=(ln2−2)−(−1.5)=ln2−2+1.5=ln2−21
所以,面积
S=ln2−21
。
选择题
本题共5小题,每小题3分,满分15分
6
设
x→0
时
ex−(ax2+bx+1)
是比
x2
高阶的无穷小,则
正确答案:A【解析】
当
x→0
时,
ex−(ax2+bx+1)
是比
x2
高阶的无穷小,即
x→0limx2ex−(ax2+bx+1)=0
将
ex
泰勒展开为
ex=1+x+2x2+6x3+⋯
代入得
ex−(ax2+bx+1)=(1+x+2x2+6x3+⋯)−(ax2+bx+1)=(1−b)x+(21−a)x2+6x3+⋯
除以
x2
后:
x2ex−(ax2+bx+1)=x1−b+(21−a)+6x+⋯
为使极限为 0,必须满足
1−b=0和21−a=0
即
b=1,a=21
因此,选项 A 正确。
7
设函数
f(x)
在区间
(−δ,δ)
内有定义,
若当
x∈(−δ,δ)
时,恒有
∣f(x)∣≤x2
,
则
x=0
必是
f(x)
的
正确答案:C【解析】
由条件可知,当
x∈(−δ,δ)
时,恒有
∣f(x)∣≤x2
。
取
x=0
,则
∣f(0)∣≤0
,故
f(0)=0
。
为检验连续性,考虑极限
limx→0f(x)
。由于
∣f(x)∣≤x2且x→0limx2=0
由夹逼定理,
limx→0∣f(x)∣=0
,因此
x→0limf(x)=0=f(0),
故
f(x)
在
x=0
处连续。
为检验可导性,考虑导数定义:
f′(0)=h→0limhf(0+h)−f(0)=h→0limhf(h).
由
∣f(h)∣≤h2
,得
由于
limh→0∣h∣=0
,由夹逼定理,
故
h→0limhf(h)=0,
即
f′(0)=0
。
因此,
f(x)
在
x=0
处可导且导数为零。选项 C 正确。
8
设
f(x)
处处可导,则
正确答案:D【解析】 考虑选项A:当
limx→−∞f(x)=−∞
时,必有
limx→−∞f′(x)=−∞
。反例:
f(x)=x
,则
limx→−∞f(x)=−∞
,但
f′(x)=1
,
limx→−∞f′(x)=1=−∞
,故A错误。
考虑选项B:当
limx→−∞f′(x)=−∞
时,必有
limx→−∞f(x)=−∞
。反例:
f(x)=x2
,则
limx→−∞f′(x)=limx→−∞2x=−∞
,但
limx→−∞f(x)=limx→−∞x2=+∞=−∞
,故B错误。
考虑选项C:当
limx→+∞f(x)=+∞
时,必有
limx→+∞f′(x)=+∞
。反例:
f(x)=x
,则
limx→+∞f(x)=+∞
,但
f′(x)=1
,
limx→+∞f′(x)=1=+∞
,故C错误。
考虑选项D:当
limx→+∞f′(x)=+∞
时,必有
limx→+∞f(x)=+∞
。证明:由于
limx→+∞f′(x)=+∞
,存在
N
,当
x>N
时,
f′(x)>1
。则对于
x>N
,有
f(x)−f(N)=∫Nxf′(t)dt>∫Nx1dt=x−N
。因此
f(x)>f(N)+x−N
。当
x→+∞
时,
x−N→+∞
,故
f(x)→+∞
。因此D正确。
9
在区间
(−∞,+∞)
内,
方程
∣x∣41+∣x∣21−cosx=0
正确答案:C【解析】
考虑函数
f(x)=∣x∣41+∣x∣21−cosx,
由于
f(−x)=f(x)
,函数为偶函数,只需分析
x≥0
的情况。
令
g(x)=x41+x21−cosx.
在
x=0
处,
g(0)=−1<0
。
设
h(x)=x41+x21
,解方程
h(x)=1
。
令
t=x41
,则
t2+t−1=0,
解得
对应
x0=t4≈0.146.
此时
g(x0)=1−cosx0>0.
由中间值定理,在
(0,x0)
内至少有一个实根。
对于
x>x0
,有
h(x)>1
,故
g(x)=h(x)−cosx≥h(x)−1>0,
因此无实根。
同时,在
(0,x0)
上,导数
g′(x)=41x−43+21x−21+sinx>0,
函数严格递增,因此仅有一个实根。
由偶函数性质,在
x<0
时有一个对称实根。
综上,方程在
(−∞,+∞)
内有且仅有两个实根。
10
设
f(x)
,
g(x)
在区间
[a,b]
上连续,
g(x)<f(x)<m
(
m
为常数),
由曲线
y=g(x)
,
y=f(x)
,
x=a
及
x=b
所围平面图形绕直线
y=m
旋转而成的旋转体体积为
正确答案:B【解析】 由曲线
y=g(x)
,
y=f(x)
,
x=a
及
x=b
所围平面图形绕直线
y=m
旋转时,对于任意
x∈[a,b]
,由于
g(x)<f(x)<m
,点
(x,g(x))
到直线
y=m
的距离为
m−g(x)
,点
(x,f(x))
到直线
y=m
的距离为
m−f(x)
。旋转后形成圆环,外半径为
m−g(x)
,内半径为
m−f(x)
。圆环的面积为
π[(m−g(x))2−(m−f(x))2]
。因此旋转体体积为:
V=∫abπ[(m−g(x))2−(m−f(x))2]dx
简化被积表达式:
[(m−g(x))2−(m−f(x))2]=[m2−2mg(x)+g(x)2−(m2−2mf(x)+f(x)2)]=2m[f(x)−g(x)]+[g(x)2−f(x)2]
其中
g(x)2−f(x)2=−[f(x)−g(x)][f(x)+g(x)]
,所以:
2m[f(x)−g(x)]−[f(x)−g(x)][f(x)+g(x)]=[f(x)−g(x)][2m−f(x)−g(x)]
因此:
V=∫abπ[f(x)−g(x)][2m−f(x)−g(x)]dx
这与选项 B 一致。
计算题
本题共6小题,每小题5分,满分30分
11
计算
∫0ln21−e−2xdx
.
【答案】
【解析】
考虑积分
I=∫0ln21−e−2xdx
。令
u=e−x
,则
du=−e−xdx=−udx
,所以
dx=−udu
。当
x=0
时,
u=1
;当
x=ln2
时,
u=e−ln2=21
。积分变为:
I=∫11/21−u2⋅(−udu)=∫1/21u1−u2du. 计算
J=∫u1−u2du
。令
u=sinθ
,则
du=cosθdθ
,且
1−u2=cosθ
(因为
θ∈[0,π/2]
)。于是:
J=∫sinθcosθ⋅cosθdθ=∫sinθcos2θdθ=∫(cscθ−sinθ)dθ=ln∣cscθ−cotθ∣+cosθ+C.
回代
u=sinθ
,有
cscθ=u1
,
cotθ=u1−u2
,
cosθ=1−u2
,所以:
因此:
I=[lnu1−1−u2+1−u2]u=1/2u=1. 在
u=1
时:
值为 0。在
u=1/2
时:
1−(1/2)2=3/4=23,ln1/21−3/2=ln∣2−3∣=ln(2−3), 值为
ln(2−3)+23
。所以:
I=0−(ln(2−3)+23)=−ln(2−3)−23. 注意到
2−3=2+31
,所以
−ln(2−3)=ln(2+3)
。因此:
此即所求积分值。
12
∫1+sinxdx=
【答案】
tanx−secx+C
【解析】
为了求解积分
∫1+sinxdx
,首先分子分母同时乘以
1−sinx
,得到:
∫1+sinxdx=∫(1+sinx)(1−sinx)1−sinxdx=∫1−sin2x1−sinxdx.
利用三角恒等式
1−sin2x=cos2x
,积分化为:
∫cos2x1−sinxdx=∫(cos2x1−cos2xsinx)dx.
分别计算两个积分:
∫cos2x1dx=∫sec2xdx=tanx,
和
∫cos2xsinxdx.
令
u=cosx
,则
du=−sinxdx
,即
dx=−sinxdu
,代入得:
∫cos2xsinxdx=∫u2sinx(−sinxdu)=−∫u−2du=−(−u−1)=u1=secx.
因此,原积分为:
tanx−secx+C.
13
设
{x=∫0tf(u2)du,y=[f(t2)]2,
其中
f(u)
具有二阶导数,且
f(u)=0
,求
dx2d2y.
【答案】
dx2d2y=f(t2)4[f′(t2)+2t2f′′(t2)]
【解析】
给定参数方程:
x=∫0tf(u2)du,y=[f(t2)]2
其中
f(u)
具有二阶导数且
f(u)=0
。
首先,求
dtdx
和
dtdy
:
dtdx=f(t2)
dtdy=2[f(t2)]⋅f′(t2)⋅2t=4tf(t2)f′(t2)
然后,求一阶导数
dxdy
:
dxdy=dx/dtdy/dt=f(t2)4tf(t2)f′(t2)=4tf′(t2)
接着,求二阶导数
dx2d2y
:
dx2d2y=dxd(dxdy)=dtdxdtd(dxdy)
计算
dtd(dxdy)
:
dtd(4tf′(t2))=4[f′(t2)+t⋅dtd[f′(t2)]]=4[f′(t2)+t⋅f′′(t2)⋅2t]=4[f′(t2)+2t2f′′(t2)]
代入:
dx2d2y=f(t2)4[f′(t2)+2t2f′′(t2)]
因此,得到最终结果。
14
求函数
f(x)=1+x1−x
在
x=0
点处带拉格朗日型余项的
n
阶泰勒展开式.
【答案】
函数
f(x)=1+x1−x
在
x=0
处带拉格朗日型余项的
n
阶泰勒展开式为:
f(x)=1+2k=1∑n(−1)kxk+(1+ξ)n+2(−1)n+12xn+1
其中
ξ
在
0
与
x
之间。
【解析】
首先,计算函数在
x=0
处的值:
f(0)=1+01−0=1
。
求各阶导数并计算在
x=0
处的值。通过求导发现规律:对于
k≥1
,有
f(k)(0)=(−1)k⋅2⋅k!
。
因此,泰勒展开的主部为:
f(x)=f(0)+k=1∑nk!f(k)(0)xk=1+k=1∑n(−1)k⋅2⋅xk
即:
f(x)=1+2k=1∑n(−1)kxk
拉格朗日型余项为:
Rn(x)=(n+1)!f(n+1)(ξ)xn+1
其中
f(n+1)(x)=(−1)n+1⋅2⋅(n+1)!⋅(1+x)−(n+2)
,代入得:
Rn(x)=(n+1)!(−1)n+1⋅2⋅(n+1)!⋅(1+ξ)−(n+2)xn+1=(−1)n+1⋅2⋅(1+ξ)−(n+2)xn+1
因此,完整展开式如上所述。
此外,函数可写为
f(x)=1+x2−1
,其几何级数展开与上述结果一致。
15
求微分方程
y′′+y′=x2
的通解.
【答案】
y=C1+C2e−x+31x3−x2+2x
,其中
C1
和
C2
为任意常数。
【解析】
给定微分方程
y′′+y′=x2
,首先求解齐次方程
y′′+y′=0
。特征方程为
r2+r=0
,解得
r=0
和
r=−
,因此齐次解为
yh=C1+C2e−x
。
接下来求非齐次方程的特解。由于非齐次项
x2
是二次多项式,且特征根
r=0
是单根,特解形式应设为
yp=x(Ax2+Bx+C)=Ax3+Bx2+Cx
。求导得
yp′=3Ax2+2Bx+C
,
yp′′=6Ax+2B
。代入原方程:
yp′′+yp′=(6Ax+2B)+(3Ax2+2Bx+C)=3Ax2+(6A+2B)x+(2B+C)
令其等于
x2
:
3A=1,6A+2B=0,2B+C=0
解得
A=31
,
B=−1
,
C=2
。因此特解为
yp=31x3−x2+2x
。
通解为齐次解与特解之和:
y=yh+yp=C1+C2e−x+31x3−x2+2x
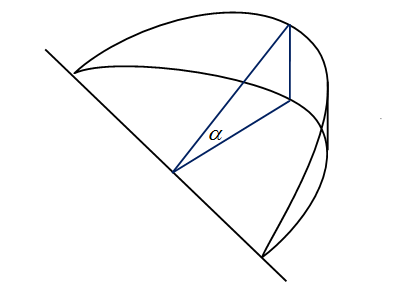
16
设有一正椭圆柱体,其底面的长、短轴分别为
2a
,
2b
,
用过此柱体底面的短轴与底面成
α
角(
0<α<2π
)的平面截此柱体,
得一锲形体(如图),求此锲形体的体积
V
.
【答案】
V=32a2btanα
【解析】
考虑正椭圆柱体,其底面椭圆方程为
a2x2+b2y2=1
,长轴为
2a
,短轴为
2b
。截面平面通过短轴(即
y
轴)且与底面成
α
角,其方程为
z=xtanα
。楔形体为柱体在
x≥0
部分介于底面
z=0
和平面
z=xtanα
之间的区域。
体积
V
可通过二重积分计算:
V=∬Dxtanαdxdy
其中
D
为半椭圆区域
a2x2+b2y2≤1
且
x≥0
。提取常数
tanα
,得:
V=tanα∬Dxdxdy
计算积分
I=∬Dxdxdy
。对于固定
x
,
y
的范围为
−b1−a2x2
至
b1−a2x2
,因此:
I=∫0a∫−b1−a2x2b1−a2x2xdydx=∫0ax⋅2b1−a2x2dx=2b∫0ax1−a2x2dx 令
t=ax
,则
x=at
,
dx=adt
,积分限变为
t=0
至
t=1
:
I=2b∫01at⋅1−t2⋅adt=2a2b∫01t1−t2dt 计算积分
∫01t1−t2dt
。令
u=1−t2
,则
du=−2tdt
,即
tdt=−21du
。当
t=0
时
u=1
,当
t=1
时
u=0
:
∫01t1−t2dt=∫10u⋅(−21)du=21∫01u1/2du=21⋅32u3/201=31 因此:
I=2a2b⋅31=32a2b
V=tanα⋅32a2b=32a2btanα
此即楔形体的体积。
解答题
17
计算不定积分
∫x2(1+x2)arctanxdx
.
【答案】
∫x2(1+x2)arctanxdx=−xarctanx−21(arctanx)2+ln∣x∣−21ln(1+x2)+C
【解析】
考虑使用分部积分法,设
u=arctanx
,则
du=1+x21dx
,而
dv=x2(1+x2)1dx
。首先计算
v=∫x2(1+x2)1dx
。通过部分分式分解,有:
x2(1+x2)1=x21−1+x21
所以:
v=∫(x21−1+x21)dx=−x1−arctanx
应用分部积分公式:
∫x2(1+x2)arctanxdx=uv−∫vdu=arctanx⋅(−x1−arctanx)−∫(−x1−arctanx)⋅1+x21dx
简化得:
=−xarctanx−(arctanx)2+∫(x(1+x2)1+1+x2arctanx)dx
计算积分
∫x(1+x2)1dx
。通过部分分式分解:
x(1+x2)1=x1−1+x2x
所以:
∫x(1+x2)1dx=∫(x1−1+x2x)dx=ln∣x∣−21ln(1+x2)
再计算积分
∫1+x2arctanxdx
。令
t=arctanx
,则
dt=1+x21dx
,所以:
∫1+x2arctanxdx=∫tdt=21t2=21(arctanx)2
将结果代回:
∫x2(1+x2)arctanxdx=−xarctanx−(arctanx)2+ln∣x∣−21ln(1+x2)+21(arctanx)2+C
合并同类项:
=−xarctanx−21(arctanx)2+ln∣x∣−21ln(1+x2)+C
此结果已验证正确。
18
设函数
f(x)=⎩⎨⎧1−2x2,x3,12x−16,x<−1,−1≤x≤2,x>2.
(1) 写出
f(x)
的反函数
g(x)
的表达式;
(2)
g(x)
是否有间断点、不可导点,若有,指出这些点.
【答案】
(1)
g(x)=⎩⎨⎧−21−x,3x,12x+16,x<−1,−1≤x≤8,x>8.
(2)
g(x)
有不可导点,在
x=−1
和
x=0
处不可导;没有间断点。
【解析】
对于(1),求反函数
g(x)
。原函数
f(x)
是单调的,反函数存在。根据
f(x)
的分段定义,反函数
g(x)
也分段定义:
- 当
x<−1
时,
f(x)=1−2x2
,解得
x=−21−f(x)
,所以
g(x)=−21−x
;
- 当
−1≤x≤2
时,
f(x)=x3
,解得
x=3f(x)
,所以
g(x)=3x
;
- 当
x>2
时,
f(x)=12x−16
,解得
x=12f(x)+16
,所以
g(x)=12x+16
。
值域对应:当
x<−1
时,
f(x)<−1
;当
−1≤x≤2
时,
f(x)∈[−1,8]
;当
x>2
时,
f(x)>8
。因此
g(x)
的定义域为全体实数,分段如答案所示。
对于(2),检查
g(x)
的连续性和可导性。
连续性:在
x=−1
处,
x→−1−limg(x)x→−1+limg(x)=−21−(−1)=−1,=3−1=−1, 且
g(−1)=−1
,故连续;在
x=8
处,
x→8−limg(x)x→8+limg(x)=38=2,=128+16=2, 且
g(8)=2
,故连续;其他点在各段内连续。因此
g(x)
无间断点。
可导性:在
x<−1
时,
g′(x)=41−x2
;在
−1<x<8
时,
g′(x)=31x−2/3
;在
x>8
时,
g′(x)=121
。
在
x=−1
处,
g−′(−1)g+′(−1)=41−(−1)2=41,=31(−1)−2/3=31, 左右导数不相等,故不可导;
在
x=0
处,
g′(x)=31x−2/3
在
x=0
处不存在,故不可导;
在
x=8
处,
g−′(8)g+′(8)=31⋅8−2/3=121,=121,
相等,故可导。
因此,不可导点为
x=−1
和
x=0
。
19
设函数
y=y(x)
由方程
2y3−2y2+2xy−x2=1
所确定,试求
y=y(x)
的驻点,并判别它是否为极值点.
【答案】
驻点为
x=1
,且是极小值点。
【解析】
由方程
2y3−2y2+2xy−x2=1
所确定的函数
y=y(x)
,通过隐函数求导,得到一阶导数:
y′=3y2−2y+xx−y.
令
y′=0
,得
x−y=0
,即
x=y
。代入原方程:
2y3−2y2+2y⋅y−y2=2y3−y2=1,
即
2y3−y2−1=0
。解得
y=1
(因为
y=1
是根,且二次因子
2y2+y+1
无实根),所以
x=1
。因此,驻点为
(1,1)
,即
x=1
。
为判断极值点,求二阶导数。由
y′=3y2−2y+xx−y
,求导得:
y′′=(3y2−2y+x)2(1−y′)(3y2−2y+x)−(x−y)(6yy′−2y′+1).
在点
(1,1)
处,
y′=0
,代入得:
y′′=(3⋅12−2⋅1+1)2(1−0)(3⋅12−2⋅1+1)−(1−1)(6⋅1⋅0−2⋅0+1)=221⋅(3−2+1)−0=42=21>0.
由于
y′′>0
,因此驻点
x=1
是极小值点。
20
设
f(x)
在区间
[a,b]
上具有二阶导数,且
f(a)=f(b)=0
,
f′(a)f′(b)>0
.
试证明:存在
ξ∈(a,b)
,
η∈(a,b)
,使
f(ξ)=0
及
f′′(η)=0
.
【解析】
首先,证明存在
ξ∈(a,b)
使
f(ξ)=0
。
由条件
f′(a)f′(b)>0
,可知
f′(a)
与
f′(b)
同号。
- 若
f′(a)>0
且
f′(b)>0
,则由于
f(a)=0
,在
a
附近有
f(x)>0
;由于
f(b)=0
,在
b
附近有
f(x)<0
。
- 若
f′(a)<0
且
f′(b)<0
,则由于
f(a)=0
,在
a
附近有
f(x)<0
;由于
f(b)=0
,在
b
附近有
f(x)>0
。
在两种情况下,函数在
a
和
b
附近符号相反,且
f(x)
在
[a,b]
上连续,由中间值定理可知,存在
ξ∈(a,b)
使
f(ξ)=0
。
其次,证明存在
η∈(a,b)
使
f′′(η)=0
。
由上可知,存在
ξ∈(a,b)
使
f(ξ)=0
,因此
f(x)
在
[a,b]
上有三个零点:
a
、
ξ
、
b
。
对
f(x)
在区间
[a,ξ]
和
[ξ,b]
上分别应用罗尔定理:
存在
c1∈(a,ξ)
使
f′(c1)=0
,存在
c2∈(ξ,b)
使
f′(c2)=0
。
再对
f′(x)
在区间
[c1,c2]
上应用罗尔定理:
由于
f′(c1)=f′(c2)=0
,且
f′(x)
在
[c1,c2]
上可导,存在
η∈(c1,c2)⊂(a,b)
使
f′′(η)=0
。
综上,结论得证。
21
设
f(x)
为连续函数,
(1) 求初值问题
{y′+ay=f(x),y∣x=0=0
的解
y(x)
,其中
a
是正常数.
(2) 若
∣f(x)∣≤k
(
k
为常数),
证明:当
x≥0
时,有
∣y(x)∣≤ak(1−e−ax)
.
【答案】
(1)
y(x)=e−ax∫0xeasf(s)ds
(2) 证明见解析。
【解析】
(1) 对于初值问题
y′+ay=f(x)
,
y(0)=0
,使用积分因子法。积分因子为
eax
。将原方程乘以积分因子得:
eaxy′+aeaxy=eaxf(x)
即
dxd(eaxy)=eaxf(x)
两边积分从 0 到
x
:
eaxy(x)−ea⋅0y(0)=∫0xeasf(s)ds
代入
y(0)=0
得:
eaxy(x)=∫0xeasf(s)ds
因此
y(x)=e−ax∫0xeasf(s)ds
(2) 已知
∣f(x)∣≤k
,需证
∣y(x)∣≤ak(1−e−ax)
对于
x≥0
。由解的形式:
∣y(x)∣=e−ax∫0xeasf(s)ds=e−ax∫0xeasf(s)ds 利用积分不等式:
∫0xeasf(s)ds≤∫0xeas∣f(s)∣ds≤∫0xeaskds=k∫0xeasds 计算积分:
∫0xeasds=a1[eas]0x=a1(eax−1)
因此
∫0xeasf(s)ds≤ak(eax−1) 代入得:
∣y(x)∣≤e−ax⋅ak(eax−1)=ak(1−e−ax)
证毕。