卷 3

填空题

本题共5小题，每小题3分，满分15分

1

设曲线 $f(x) = x^n$ 在点 $(1,1)$ 处的切线与 $x$ 轴的交点为 $(\xi_n,0)$ ，则 $\lim_{n \to \infty} f(\xi_n) =$ ______．

【答案】
$\frac{1}{e}$

【解析】
曲线 $f(x) = x^n$ 在点 $(1,1)$ 处的切线斜率为 $f'(x) = n x^{n-1}$ ，在 $x=1$ 处斜率为 $n$ 。切线方程为 $y - 1 = n(x - 1)$ 。
切线与 $x$ 轴交于 $(\xi_n, 0)$ ，代入得 $0 - 1 = n(\xi_n - 1)$ ，解得 $\xi_n = 1 - \frac{1}{n}$ 。
则 $f(\xi_n) = \left(1 - \frac{1}{n}\right)^n$ 。
求极限

\lim_{n \to \infty} f(\xi_n) = \lim_{n \to \infty} \left(1 - \frac{1}{n}\right)^n = e^{-1} = \frac{1}{e}

2

$\int \frac{\ln x - 1}{x^2} \dx =$ ______．

高等数学一元函数积分学不定积分的计算

【答案】
$-\frac{\ln x}{x} + C$

【解析】
考虑积分 $\int \frac{\ln x - 1}{x^2} \, dx$ 。使用分部积分法，设 $u = \ln x - 1$ ， $dv = \frac{1}{x^2} \, dx$ ，则 $du = \frac{1}{x} \, dx$ ， $v = -\frac{1}{x}$ 。代入分部积分公式：

\begin{align*} \int u \, dv &= uv - \int v \, du \\ &= (\ln x - 1) \cdot \left(-\frac{1}{x}\right) - \int \left(-\frac{1}{x}\right) \cdot \frac{1}{x} \, dx \\ &= -\frac{\ln x - 1}{x} + \int \frac{1}{x^2} \, dx. \end{align*}

其中 $\int \frac{1}{x^2} \, dx = -\frac{1}{x} + C$ ，所以：

-\frac{\ln x - 1}{x} - \frac{1}{x} + C = -\frac{\ln x}{x} + C.

因此，积分结果为 $-\frac{\ln x}{x} + C$ 。
验证：对 $-\frac{\ln x}{x}$ 求导，

\frac{d}{dx} \left( -\frac{\ln x}{x} \right) = -\frac{\frac{1}{x} \cdot x - \ln x \cdot 1}{x^2} = -\frac{1 - \ln x}{x^2} = \frac{\ln x - 1}{x^2},

与原被积函数一致。

3

差分方程 $2y_{t + 1} + 10y_t - 5t = 0$ 的通解为 ______．

高等数学常微分方程其他方程

【答案】
$y_t = A \cdot (-5)^t + \frac{5}{12}t - \frac{5}{72}$

【解析】
给定差分方程 $2y_{t+1} + 10y_t - 5t = 0$ ，可化为标准形式

y_{t+1} + 5y_t = \frac{5}{2}t .

齐次方程

y_{t+1} + 5y_t = 0

的解为

y_h = A \cdot (-5)^t ,

其中 $A$ 为常数。

非齐次项为 $\frac{5}{2}t$ ，设特解形式为

y_p = at + b .

代入方程：

y_{t+1} = a(t+1) + b = at + a + b ,

代入得

(at + a + b) + 5(at + b) = 6at + (a + 6b) = \frac{5}{2}t .

比较系数：

6a = \frac{5}{2}, \quad \text{解得} \quad a = \frac{5}{12};

a + 6b = 0, \quad \text{即} \quad \frac{5}{12} + 6b = 0, \quad \text{解得} \quad b = -\frac{5}{72}.

特解为

y_p = \frac{5}{12}t - \frac{5}{72}.

通解为齐次解与特解之和：

y_t = A \cdot (-5)^t + \frac{5}{12}t - \frac{5}{72}.

4

设矩阵 $A,B$ 满足 $A^* BA = 2BA - 8E$ ，其中 $A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ , $E$ 为单位矩阵， $A^*$ 为 $A$ 的伴随矩阵，则 $B =$ ______．

线性代数矩阵伴随矩阵与可逆矩阵

【答案】

B = \begin{pmatrix} 2 & 0 & 0 \\ 0 & -4 & 0 \\ 0 & 0 & 2 \end{pmatrix}

【解析】 应填

\begin{pmatrix} 2 & 0 & 0 \\ 0 & -4 & 0 \\ 0 & 0 & 2 \end{pmatrix}

由于 $|A| = -2 \neq 0$ ，所以 $A$ 可逆。在 $A^*BA = 2BA - 8E$ 两边左乘 $A$ ，右乘 $A^{-1}$ ，利用公式 $AA^* = |A|E, AA^{-1} = E$ ，得到 $|A|B = 2AB - 8E$ 。

$|A| = -2$ 代入上式，整理得

B = 4(E + A)^{-1} = 4 \begin{pmatrix} 2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 2 \end{pmatrix}^{-1} = 4 \begin{pmatrix} \frac{1}{2} & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & \frac{1}{2} \end{pmatrix} = \begin{pmatrix} 2 & 0 & 0 \\ 0 & -4 & 0 \\ 0 & 0 & 2 \end{pmatrix}

5

设 $X_1,X_2,X_3,X_4$ 是来自正态总体 $N\left(0,2^2 \right)$ 的简单随机样本，

X = a\left(X_1 - 2X_2 \right)^2 + b\left(3X_3 - 4X_4 \right)^2,

则当 $a=$ ______, $b=$ ______时，统计量 $X$ 服从 $\chi^2$ 分布，其自由度为 ______．

概率论与数理统计随机变量及其分布

【答案】 $a = \frac{1}{20}$ , $b = \frac{1}{100}$ , 自由度为 2

【解析】 由于 $X_1, X_2, X_3, X_4$ 相互独立，均服从 $N(0, 2^2)$ ，所以由数学期望和方差的性质，得

E(X_1 - 2X_2) = 0, \quad D(X_1 - 2X_2) = 1 \times 2^2 + 2^2 \times 2^2 = 20,

所以 $X_1 - 2X_2 \sim N(0, 20)$ ，同理 $3X_3 - 4X_4 \sim N(0, 100)$ 。又因为 $X_1 - 2X_2$ 与 $3X_3 - 4X_4$ 相互独立，且

\frac{1}{\sqrt{20}}(X_1 - 2X_2) \sim N(0, 1), \quad \frac{1}{\sqrt{100}}(3X_3 - 4X_4) \sim N(0, 1),

由 $\chi^2$ 分布的定义，当 $a = \frac{1}{20}, b = \frac{1}{100}$ 时，

X = \frac{1}{20}(X_1 - 2X_2)^2 + \frac{1}{100}(3X_3 - 4X_4)^2 \sim \chi^2(2);

即当 $a = \frac{1}{20}, b = \frac{1}{100}$ 时， $X$ 服从 $\chi^2$ 分布，其自由度为 2。实际上，当 $a = 0, b = \frac{1}{100}$ 时， $X \sim \chi^2(1)$ ；当 $a = \frac{1}{20}, b = 0$ 时， $X \sim \chi^2(1)$ ，也是正确的。

选择题

本题共5小题，每小题3分，共15分

6

设周期函数 $f(x)$ 在 $\left(-\infty , +\infty \right)$ 内可导，周期为 $4$ ．又 $\lim_{x \to 0} \frac{f(1) - f(1 - x)}{2x} = - 1$ ，则曲线 $y = f(x)$ 在点 $\left(5,f(5) \right)$ 处的切线的斜率为

高等数学一元函数微分学导数的几何意义

正确答案：D

【解析】 由于 $f(x)$ 周期为 4 且可导，因此 $f'(x)$ 也周期为 4，即 $f'(x+4) = f'(x)$ 。给定极限 $\lim_{x \to 0} \frac{f(1) - f(1 - x)}{2x} = -1$ ，令 $h = -x$ ，则当 $x \to 0$ 时 $h \to 0$ ，有：

\frac{f(1) - f(1 - x)}{2x} = \frac{- [f(1 + h) - f(1)]}{-2h} = \frac{f(1 + h) - f(1)}{2h},

所以

\lim_{h \to 0} \frac{f(1 + h) - f(1)}{2h} = \frac{1}{2} f'(1) = -1,

解得 $f'(1) = -2$ 。由周期性， $f'(5) = f'(1) = -2$ ，因此曲线在点 $(5, f(5))$ 处的切线斜率为 $-2$ 。

7

设函数 $f(x) = \lim_{n \to \infty} \frac{1 + x}{1 + x^{2n}}$ ，讨论函数 $f(x)$ 的间断点，其结论为

高等数学函数、极限、连续函数极限的计算

正确答案：B

【解析】 函数

f(x) = \lim_{n \to \infty} \frac{1 + x}{1 + x^{2n}}

的极限依赖于 $x$ 的值。

当 $|x| < 1$ 时， $x^{2n} \to 0$ ，故 $f(x) = 1 + x$ ；
当 $|x| > 1$ 时， $x^{2n} \to \infty$ ，故 $f(x) = 0$ ；
当 $x = 1$ 时， $f(1) = \lim_{n \to \infty} \frac{2}{1 + 1} = 1$ ；
当 $x = -1$ 时， $f(-1) = \lim_{n \to \infty} \frac{0}{1 + 1} = 0$ 。

在 $x = 1$ 处，左极限为

\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (1 + x) = 2,

右极限为

\lim_{x \to 1^+} f(x) = 0,

函数值为 $f(1) = 1$ ，三者不相等，故 $x = 1$ 为间断点。

在 $x = -1$ 处，左极限、右极限和函数值均为 0，故连续。
在 $x = 0$ 处，函数连续。

因此，存在间断点 $x = 1$ ，对应选项 B。

8

齐次线性方程组 $\begin{cases} \lambda x_1 + x_2 + \lambda^2x_3 = 0, \\ x_1 + \lambda x_2 + x_3 = 0, \\ x_1 + x_2 + \lambda x_3 = 0 \end{cases}$ 的系数矩阵记为 $A$ ．若存在三阶矩阵 $B \ne 0$ 使得 $AB = 0$ ，则

线性代数线性方程组

正确答案：C

【解析】 齐次线性方程组的系数矩阵为 $A = \begin{pmatrix} \lambda & 1 & \lambda^2 \\ 1 & \lambda & 1 \\ 1 & 1 & \lambda \end{pmatrix}$ 。存在三阶矩阵 $B \ne 0$ 使得 $AB = 0$ ，这意味着 $B$ 的列向量均为 $Ax = 0$ 的解，因此 $A$ 必须奇异，即 $|A| = 0$ 。计算 $|A|$ ：

\begin{align*} |A| &= \begin{vmatrix} \lambda & 1 & \lambda^2 \\ 1 & \lambda & 1 \\ 1 & 1 & \lambda \end{vmatrix} \\ &= \lambda (\lambda^2 - 1) - 1 (\lambda - 1) + \lambda^2 (1 - \lambda) \\ &= \lambda^3 - \lambda - \lambda + 1 + \lambda^2 - \lambda^3 \\ &= \lambda^2 - 2\lambda + 1 \\ &= (\lambda - 1)^2. \end{align*}

设 $|A| = 0$ ，得 $\lambda = 1$ 。当 $\lambda = 1$ 时， $A = \begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix}$ ，方程组化为 $x_1 + x_2 + x_3 = 0$ ，解空间为二维。 $B$ 的列向量均属于该二维子空间，因此三列线性相关，故 $|B| = 0$ 。选项 A 和 B 中 $\lambda = -2$ 时 $|A| \ne 0$ ，不可能存在 $B \ne 0$ 使 $AB = 0$ ；选项 D 中 $|B| \ne 0$ 不成立。因此正确选项为 C。

9

设 $n\left(n \ge 3 \right)$ 阶矩阵 $A = \begin{pmatrix} 1 & a & a & \cdots & a \\ a & 1 & a & \cdots & a \\ a & a & 1 & \cdots & a \\ \vdots & \vdots & \vdots & & \vdots \\ a & a & a & \cdots & 1 \end{pmatrix}$ ，若矩阵 $A$ 的秩为 $n - 1$ ，则 $a$ 必为

线性代数矩阵矩阵的秩

正确答案：B

【解析】
矩阵 $A$ 的秩为 $n-1$ ，因此其行列式为零。矩阵 $A$ 可表示为

A = (1 - a) I + a J

其中 $I$ 是单位矩阵， $J$ 是全 1 矩阵。计算行列式，特征值分别为

1 + a(n-1) \quad \text{和} \quad 1 - a \; (\text{重数 } n-1)

故

\det(A) = [1 + a(n-1)] (1 - a)^{n-1} = 0

解得

a = 1 \quad \text{或} \quad a = -\frac{1}{n-1}

当 $a = 1$ 时，矩阵所有元素均为 1，秩为 1，不满足条件。
当 $a = -\frac{1}{n-1}$ 时，特征值

1 + a(n-1) = 0

其余特征值非零，秩为 $n-1$ ，符合要求。
选项 B 为 $\frac{1}{1-n} = -\frac{1}{n-1}$ ，故正确。

10

设 $F_1(x)$ 与 $F_2(x)$ 分别为随机变量 $X_1$ 与 $X_2$ 的分布函数．为使 $F(x) = aF_1(x) - bF_2(x)$ 是某一变量的分布函数，在下列给定的各组数值中应取

概率论与数理统计随机变量及其分布

正确答案：A

【解析】
为了使 $F(x) = aF_1(x) - bF_2(x)$ 是某一随机变量的分布函数，必须满足分布函数的条件：非递减性、右连续性，以及

\lim_{x \to -\infty} F(x) = 0,\quad \lim_{x \to \infty} F(x) = 1.

由于 $F_1(x)$ 和 $F_2(x)$ 是分布函数，它们满足这些条件，因此右连续性自动满足。

首先考虑极限条件：当 $x \to \infty$ 时， $F_1(x) \to 1$ ， $F_2(x) \to 1$ ，所以

F(x) \to a \cdot 1 - b \cdot 1 = a - b,

必须等于 1，即

a - b = 1.

其次考虑非递减性：对于任意 $x_1 < x_2$ ，有 $F(x_1) \leq F(x_2)$ ，即

a\big[F_1(x_2) - F_1(x_1)\big] - b\big[F_2(x_2) - F_2(x_1)\big] \geq 0.

由于 $F_1$ 和 $F_2$ 非递减，其增量 $\Delta F_1 \geq 0$ 和 $\Delta F_2 \geq 0$ 。要保证不等式恒成立，需

a \geq 0,\quad b \leq 0.

检查选项：

A： $a = \dfrac{3}{5},\; b = -\dfrac{2}{5}$ ，满足 $a - b = 1$ ，且 $a \geq 0,\; b \leq 0$ 。
B： $a = \dfrac{2}{3},\; b = \dfrac{2}{3}$ ，不满足 $a - b = 1$ ，且 $b > 0$ 。
C： $a = -\dfrac{1}{2},\; b = \dfrac{3}{2}$ ，不满足 $a - b = 1$ ，且 $a < 0,\; b > 0$ 。
D： $a = \dfrac{1}{2},\; b = -\dfrac{3}{2}$ ，满足 $a \geq 0,\; b \leq 0$ ，但不满足 $a - b = 1$ 。

因此，只有选项 A 满足所有条件。

解答题

11

设 $z = (x^2 + y^2)\e^{- \arctan \frac{y}{x}}$ ，求 $\dz$ 与 $\frac{\pd^2 z}{\pdx\pd y}$ ．

高等数学多元函数微分学偏导数的概念与计算

【答案】

\dz = e^{-\arctan \frac{y}{x}} \left( (2x + y) \dx + (2y - x) \dy \right)

\frac{\pd^2 z}{\pdx\pd y} = e^{-\arctan \frac{y}{x}} \frac{ y^2 - x^2 - x y }{x^2 + y^2}

【解析】 设 $z = (x^2 + y^2) e^{-\arctan \frac{y}{x}}$ 。首先求全微分 $\dz$ ，需计算一阶偏导数 $\frac{\pd z}{\pd x}$ 和 $\frac{\pd z}{\pd y}$ 。

令 $u = \arctan \frac{y}{x}$ ，则 $z = (x^2 + y^2) e^{-u}$ 。
计算 $\frac{\pd z}{\pd x}$ :

\frac{\pd z}{\pd x} = \frac{\pd}{\pd x} \left( (x^2 + y^2) e^{-u} \right) = 2x e^{-u} + (x^2 + y^2) e^{-u} \left( -\frac{\pd u}{\pd x} \right)

其中 $\frac{\pd u}{\pd x} = \frac{\pd}{\pd x} \arctan \frac{y}{x} = \frac{1}{1 + (y/x)^2} \cdot \left( -\frac{y}{x^2} \right) = -\frac{y}{x^2 + y^2}$ ，
代入得：

\frac{\pd z}{\pd x} = 2x e^{-u} + (x^2 + y^2) e^{-u} \left( \frac{y}{x^2 + y^2} \right) = e^{-u} (2x + y)

计算 $\frac{\pd z}{\pd y}$ :

\frac{\pd z}{\pd y} = \frac{\pd}{\pd y} \left( (x^2 + y^2) e^{-u} \right) = 2y e^{-u} + (x^2 + y^2) e^{-u} \left( -\frac{\pd u}{\pd y} \right)

其中 $\frac{\pd u}{\pd y} = \frac{\pd}{\pd y} \arctan \frac{y}{x} = \frac{1}{1 + (y/x)^2} \cdot \frac{1}{x} = \frac{x}{x^2 + y^2}$ ，
代入得：

\frac{\pd z}{\pd y} = 2y e^{-u} - (x^2 + y^2) e^{-u} \frac{x}{x^2 + y^2} = e^{-u} (2y - x)

因此，全微分为：

\begin{align*} \dz &= \frac{\pd z}{\pd x} \dx + \frac{\pd z}{\pd y} \dy \\ &= e^{-u} (2x + y) \dx + e^{-u} (2y - x) \dy \\ &= e^{-\arctan \frac{y}{x}} \left( (2x + y) \dx + (2y - x) \dy \right) \end{align*}

接下来求混合偏导数 $\frac{\pd^2 z}{\pdx\pd y}$ ，即对 $\frac{\pd z}{\pd x}$ 求关于 $y$ 的偏导：

\frac{\pd^2 z}{\pdx\pd y} = \frac{\pd}{\pd y} \left( e^{-u} (2x + y) \right)

应用乘积法则：

\begin{align*} \frac{\partial}{\partial y} \left( e^{-u} (2x + y) \right) &= e^{-u} \cdot \left( -\frac{\partial u}{\partial y} \right) (2x + y) e^{-u} \cdot \frac{\partial}{\partial y} (2x + y) \\ &= e^{-u} \left( -\frac{\partial u}{\partial y} (2x + y) + 1 \right) \end{align*}

代入 $\frac{\pd u}{\pd y} = \frac{x}{x^2 + y^2}$ ：

\frac{\pd^2 z}{\pdx\pd y} = e^{-u} \left( -\frac{x}{x^2 + y^2} (2x + y) + 1 \right) = e^{-u} \frac{ -x(2x + y) + (x^2 + y^2) }{x^2 + y^2}

化简分子：

-x(2x + y) + x^2 + y^2 = -2x^2 - x y + x^2 + y^2 = -x^2 - x y + y^2

因此：

\frac{\pd^2 z}{\pdx\pd y} = e^{-u} \frac{ y^2 - x^2 - x y }{x^2 + y^2} = e^{-\arctan \frac{y}{x}} \frac{ y^2 - x^2 - x y }{x^2 + y^2}

12

设 $D = \left\{\left(x,y \right)\left| x^2 + y^2 \le x \right. \right\}$ ，求 $\iint_D \sqrt{x} \dx\dy$ ．

高等数学多元函数积分学重积分的计算

【答案】

\frac{8}{15}

【解析】
积分区域 $D$ 由 $x^2 + y^2 \le x$ 定义，可改写为 $(x - \frac{1}{2})^2 + y^2 \le \frac{1}{4}$ ，即圆心在 $(\frac{1}{2}, 0)$ 、半径为 $\frac{1}{2}$ 的圆盘。
由于被积函数 $\sqrt{x}$ 仅依赖于 $x$ ，且区域关于 $x$ 轴对称，积分可化为：

\iint_D \sqrt{x} \, dx \, dy = \int_{0}^{1} \int_{-\sqrt{x - x^2}}^{\sqrt{x - x^2}} \sqrt{x} \, dy \, dx

内层积分对 $y$ 进行：

\int_{-\sqrt{x - x^2}}^{\sqrt{x - x^2}} \sqrt{x} \, dy = \sqrt{x} \cdot 2\sqrt{x - x^2} = 2\sqrt{x} \sqrt{x(1-x)} = 2x \sqrt{1-x}

因此积分变为：

2 \int_{0}^{1} x \sqrt{1-x} \, dx

令 $u = 1 - x$ ，则 $du = -dx$ ，积分限变为 $u$ 从 $1$ 到 $0$ ：

\int_{0}^{1} x \sqrt{1-x} \, dx = \int_{1}^{0} (1-u) \sqrt{u} \, (-du) = \int_{0}^{1} (1-u) u^{1/2} \, du = \int_{0}^{1} (u^{1/2} - u^{3/2}) \, du

计算积分：

\int_{0}^{1} u^{1/2} \, du = \left[ \frac{2}{3} u^{3/2} \right]_{0}^{1} = \frac{2}{3}, \quad \int_{0}^{1} u^{3/2} \, du = \left[ \frac{2}{5} u^{5/2} \right]_{0}^{1} = \frac{2}{5}

所以：

\int_{0}^{1} (u^{1/2} - u^{3/2}) \, du = \frac{2}{3} - \frac{2}{5} = \frac{4}{15}

原积分为：

2 \times \frac{4}{15} = \frac{8}{15}

故结果为 $\frac{8}{15}$ 。

13

设某酒厂有一批新酿的好酒，如果现在（假定 $t = 0$ ）就售出，总收入为 $R_0(\text{元})$ ．如果窖藏起来待来日按陈酒价格出售， $t$ 年末总收入为 $R = R_0\e^{\frac{2}{5}\sqrt{t}}$ ．假定银行的年利率为 $r$ ，并以连续复利计息，试求窖藏多少年售出可使总收入的现值最大．并求 $r = 0.06$ 时的 $t$ 值．

高等数学一元函数微分学函数的单调性、极值与最值

【答案】
窖藏 $t = \frac{1}{25r^2}$ 年售出可使总收入的现值最大。当 $r = 0.06$ 时， $t = \frac{100}{9}$ 年。

【解析】
由连续复利公式知，这批酒在窖藏 $t$ 年末售出总收入 $R$ 的现值为 $A(t) = Re^{-rt}$ ，而由题设， $t$ 年末的总收入 $R = R_0 e^{\frac{2}{5}\sqrt{t}}$ ，从而 $A(t) = Re^{-rt} = R_0 e^{\frac{2}{5}\sqrt{t}-rt}$ 。令

\frac{dA}{dt} = R_0 e^{\frac{2}{5}\sqrt{t}-rt} \left( \frac{1}{5\sqrt{t}} - r \right) = 0,

得惟一驻点 $t = t_0 = \frac{1}{25r^2}$ 。又因为

\begin{align*} \frac{d^2A}{dt^2} &= R_0 e^{\frac{2}{5}\sqrt{t}-rt} \left( \frac{1}{5\sqrt{t}} - r \right)^2 + R_0 e^{\frac{2}{5}\sqrt{t}-rt} \left( -\frac{1}{10\sqrt{t^3}} \right) \\ &= R_0 e^{\frac{2}{5}\sqrt{t}-rt} \left[ \left( \frac{1}{5\sqrt{t}} - r \right)^2 - \frac{1}{10\sqrt{t^3}} \right], \end{align*}

从而

\frac{d^2A}{dt^2} \bigg|_{t=t_0} = R_0 e^{\frac{1}{25r}} (-12.5r^3) < 0

根据极值的第二充分条件知 $t = t_0$ 是 $A(t)$ 的极大值点。又因驻点惟一，所以也是最大值点。故窖藏 $t = \frac{1}{25r^2}$ 年出售，总收入的现值最大。当 $r = 0.06$ 时， $t = \frac{100}{9} \approx 11$ (年)。

14

设函数 $f(x)$ 在 $[a,b]$ 上连续，在 $(a,b)$ 内可导，且 $f'(x) \ne 0$ ．试证存在 $\xi,\;\eta\in(a,b)$ ，使得 $\frac{f'(\xi)}{f'(\eta)} = \frac{\e^b - \e^a}{b - a} \cdot \e^{- \eta}$ ．

高等数学一元函数微分学微分中值定理

【答案】
存在ξ, η∈(a,b)使得所述等式成立。

【解析】
由于函数 $f(x)$ 在 $[a,b]$ 上连续，在 $(a,b)$ 内可导，且 $f'(x) \ne 0$ ，根据拉格朗日中值定理，存在 $\xi \in (a,b)$ 使得

f(b) - f(a) = f'(\xi)(b - a).

考虑函数 $g(x) = e^x$ ，它在 $[a,b]$ 上连续，在 $(a,b)$ 内可导，且 $g'(x) = e^x \ne 0$ 。由柯西中值定理，存在 $\eta \in (a,b)$ 使得

\frac{f(b) - f(a)}{e^b - e^a} = \frac{f'(\eta)}{e^\eta}.

将拉格朗日中值定理的结果代入上式，得

\frac{f'(\xi)(b - a)}{e^b - e^a} = \frac{f'(\eta)}{e^\eta},

整理得

\frac{f'(\xi)}{f'(\eta)} = \frac{e^b - e^a}{b - a} \cdot e^{-\eta}.

因此，存在 $\xi, \eta \in (a,b)$ 使得所述等式成立。

15

设有两条抛物线 $y = nx^2 + \frac{1}{n}$ 和 $y = (n + 1)x^2 + \frac{1}{n + 1}$ ，记它们交点的横坐标的绝对值为 $a_n$ ．

(1) 求这两条抛物线所围成的平面图形的面积 $S_n$ ；

(2) 求级数 $\sum_{n = 1}^{\infty}\frac{S_n}{a_n}$ 的和．

高等数学一元函数积分学定积分的应用

【答案】 $\frac{4}{3}$

【解析】 (Ⅰ) 由 $y = nx^2 + \frac{1}{n}$ 与 $y = (n+1)x^2 + \frac{1}{n+1}$ 得 $a_n = \frac{1}{\sqrt{n(n+1)}}$ 。因图形关于 $y$ 轴对称，所以，所求图形的面积为

\begin{align*} S_n &= 2\int_0^{a_n} \left[ nx^2 + \frac{1}{n} - (n+1)x^2 - \frac{1}{n+1} \right] dx \\ &= 2\int_0^{a_n} \left[ -x^2 + \frac{1}{n(n+1)} \right] dx \\ &= \frac{2a_n}{n(n+1)} - \frac{2a_n^3}{3} \\ &= \frac{4}{3} \cdot \frac{1}{n(n+1)\sqrt{n(n+1)}} \end{align*}

(Ⅱ) 由 (I) 的结果知

\frac{S_n}{a_n} = \frac{4}{3}\frac{1}{n(n+1)} = \frac{4}{3}\left(\frac{1}{n} - \frac{1}{n+1}\right)

根据级数和的定义有

\sum_{n=1}^{\infty} \frac{S_n}{a_n} = \lim_{n \to \infty} \sum_{k=1}^{n} \frac{S_k}{a_k} = \frac{4}{3} \lim_{n \to \infty} \sum_{k=1}^{n} \left(\frac{1}{k} - \frac{1}{k+1}\right) = \frac{4}{3} \lim_{n \to \infty} \left[ 1 - \frac{1}{n+1} \right] = \frac{4}{3}

16

设函数 $f(x)$ 在 $[1, +\infty)$ 上连续．若由曲线 $y = f(x)$ ，直线 $x = 1,x = t\;(t > 1)$ 与 $x$ 轴所围成的平面图形绕 $x$ 轴旋转一周所形成的旋转体体积为

V(t) = \frac{\pi}{3}\left[t^2 f(t) - f(1) \right].

试求 $y = f(x)$ 所满足的微分方程，并求该微分方程满足条件 $y\big|_{x = 2} = \frac{2}{9}$ 的解．

高等数学一元函数积分学变限积分

【答案】

y = \frac{x}{1+x^3}

【解析】
由题设及旋转体体积公式得

\pi \int_{1}^{t} f^{2}(x) dx = \frac{\pi}{3} [t^{2}f(t)-f(1)] \text{ 即 } 3 \int_{1}^{t} f^{2}(x) dx = t^{2}f(t)-f(1).

两边对 $t$ 求导，化成微分方程

3f^{2}(t)=2tf(t)+t^{2}f^{\prime}(t) \text{ 即 } \frac{dy}{dx}=3\left(\frac{y}{x}\right)^{2}-2\left(\frac{y}{x}\right).

这是一阶齐次微分方程。令 $y=ux$ ，有

\frac{dy}{dx}=u+x\cdot\frac{du}{dx},

则上式化为

u+x\left(\frac{du}{dx}\right)=3u^{2}-2u \text{即 } x\frac{du}{dx}=3u(u-1).

易知当 $u=0$ 或 $u=1$ 时不满足初始条件 $y|_{x=2}=\frac{2}{9}$ ，所以 $u\neq 0$ 且 $u\neq 1$ 。将上述分离并两边积分得

\frac{du}{u(u-1)}=\frac{3dx}{x}

\Rightarrow \quad \frac{u-1}{u}=Cx^{3}.

从而微分方程的通解为 $y-x=Cx^{3}y$ （ $C$ 为任意常数）。代入初值 $y|_{x=2}=\frac{2}{9}$ 得 $C=-1$ ，从而所求的解为 $y-x=-x^{3}y$ ，即

y=\frac{x}{1+x^{3}}.

17

设向量 $\alpha = (a_1,a_2, \cdots ,a_n)^T$ , $\beta = (b_1,b_2, \cdots ,b_n)^T$ 都是非零向量，且满足条件 $\alpha^T\beta = 0$ ．记 $n$ 阶矩阵 $A = \alpha \beta^T$ ．求：

(1) $A^2$ ；

(2) 矩阵 $A$ 的特征值和特征向量．

线性代数矩阵的特征值与特征向量

【答案】
(1) $A^2 = 0$ （零矩阵）。
(2) 矩阵 $A$ 的特征值全为 0；特征向量是所有满足 $\beta^T v = 0$ 的非零向量 $v$ 。

【解析】 (Ⅰ) 对等式 $\alpha^T \beta = 0$ 两边取转置，有 $(\alpha^T \beta)^T = \beta^T \alpha = 0$ ，即 $\beta^T \alpha = 0$ 。从而

A^2 = (\alpha \beta^T)^2 = \alpha \beta^T \alpha \beta^T = \alpha (\beta^T \alpha) \beta^T = \alpha 0 \beta^T = 0 \alpha \beta^T = 0.

即 $A^2$ 是 $n$ 阶零矩阵。

(Ⅱ) 设 $\lambda$ 是 $A$ 的任一特征值， $\xi$ 是对应的特征向量（ $\xi \neq 0$ ），则有

A \xi = \lambda \xi \quad \Rightarrow \quad 0 = A^2 \xi = \lambda^2 \xi \quad \Rightarrow \quad \lambda = 0.

即矩阵的全部特征值为零。下面求 $A$ 的特征向量：不妨设 $a_1 \neq 0, b_1 \neq 0$ ，则对线性方程组 $(0E - A)x = 0$ 的系数矩阵作初等行变换得

(0E - A) = \begin{pmatrix} -a_1 b_1 & -a_1 b_2 & \cdots & -a_1 b_n \\ -a_2 b_1 & -a_2 b_2 & \cdots & -a_2 b_n \\ \vdots & \vdots & \ddots & \vdots \\ -a_n b_1 & -a_n b_2 & \cdots & -a_n b_n \end{pmatrix} \rightarrow \begin{pmatrix} b_1 & b_2 & \cdots & b_n \\ -a_2 b_1 & -a_2 b_2 & \cdots & -a_2 b_n \\ \vdots & \vdots & \ddots & \vdots \\ -a_n b_1 & -a_n b_2 & \cdots & -a_n b_n \end{pmatrix}

\rightarrow \begin{pmatrix} b_1 & b_2 & \cdots & b_n \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{pmatrix}.

于是得方程组 $(0E - A)x = 0$ 的基础解系为

\xi_1 = (-b_2, b_1, 0, \cdots, 0), \xi_2 = (-b_3, 0, b_1, \cdots, 0), \cdots, \xi_{n-1} = (-b_n, 0, 0, \cdots, b_1).

则 $A$ 的属于 $\lambda = 0$ 的全部特征向量为 $k_1 \xi_1 + k_2 \xi_2 + \cdots + k_{n-1} \xi_{n-1}$ ，其中 $k_1, k_2, \cdots, k_{n-1}$ 为不全为零的任意常数。

18

设矩阵 $A = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 2 & 0 \\ 1 & 0 & 1 \end{pmatrix}$ ，矩阵 $B = (kE + A)^2$ ，其中 $k$ 为实数， $E$ 为单位矩阵．求对角矩阵 $\Lambda$ ，使 $B$ 与 $\Lambda$ 相似，并求 $k$ 为何值时， $B$ 为正定矩阵．

线性代数矩阵的特征值与特征向量

【答案】 对角矩阵 $\Lambda = \begin{pmatrix} k^2 & 0 & 0 \\ 0 & (k+2)^2 & 0 \\ 0 & 0 & (k+2)^2 \end{pmatrix}$ ，使 $B$ 与 $\Lambda$ 相似。当 $k \neq 0$ 且 $k \neq -2$ 时， $B$ 为正定矩阵。

【解析】
由于矩阵 $A$ 的特征多项式

|\lambda E - A| = \begin{vmatrix} \lambda - 1 & 0 & -1 \\ 0 & \lambda - 2 & 0 \\ -1 & 0 & \lambda - 1 \end{vmatrix} = (\lambda - 2) \begin{vmatrix} \lambda - 1 & -1 \\ -1 & \lambda - 1 \end{vmatrix} = \lambda (\lambda - 2)^2,

可得 $A$ 的特征值是 $\lambda_1 = \lambda_2 = 2, \lambda_3 = 0$ 。因为 $A$ 是实对称矩阵，故存在可逆矩阵

P \text{ 使 } P^{-1}AP = \Lambda = \begin{pmatrix} 2 \\ & 2 \\ & & 0 \end{pmatrix},

即 $A = PAP^{-1}$ 。那么

\begin{align*} B &= (kE + A)^2 = (kPP^{-1} + PAP^{-1})^2 = [P(kE + \Lambda)P^{-1}]^2 \\ &= P(kE + \Lambda)P^{-1}P(kE + \Lambda)P^{-1} = P(kE + \Lambda)^2P^{-1}. \end{align*}

即 $P^{-1}BP = (kE + \Lambda)^2$ 。故 $B \sim \begin{pmatrix} (k+2)^2 & 0 & 0 \\ 0 & (k+2)^2 & 0 \\ 0 & 0 & k^2 \end{pmatrix}$ 。当 $k \neq -2$ 且 $k \neq 0$ 时， $B$ 的全部特征值大于零，这时 $B$ 为正定矩阵。

19

一商店经销某种商品，每周进货的数量 $X$ 与顾客对该种商品的需求量 $Y$ 是相互独立的随机变量，且都服从区间 $\left[10,20 \right]$ 上的均匀分布．商店每售出一单位商品可得利润 $1000$ 元；若需求量超过了进货量，商店可从其他商店调剂供应，这时每单位商品获利润为 $500$ 元．试计算此商店经销该种商品每周所得利润的期望值．

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

【答案】

\frac{42500}{3}

【解析】
设 $Z$ 表示商店每周所得的利润，当 $Y \leq X$ 时，卖得利润为 $Z = 1000Y$ （元）；当 $Y > X$ 时，调剂了 $Y - X$ ，总共得到利润 $Z = 1000X + 500(Y - X) = 500(X + Y)$ （元）。所以

Z = \begin{cases} 1000Y, & Y \leq X, \\ 500(X + Y), & Y > X. \end{cases}

由题设 $X$ 与 $Y$ 都服从区间 $[10, 20]$ 上的均匀分布，联合概率密度为

f(x, y) = \begin{cases} \dfrac{1}{100}, & 10 \leq x \leq 20, \ 10 \leq y \leq 20, \\ 0, & \text{其他}. \end{cases}

由二维连续型随机变量的数学期望定义得

\begin{align*} E(Z) &= \iint_{D_1} 1000y \cdot f(x, y) \, dx \, dy + \iint_{D_2} 500(x + y) \cdot f(x, y) \, dx \, dy \\ &= \iint_{D_1} 1000y \cdot \frac{1}{100} \, dx \, dy + \iint_{D_2} 500(x + y) \cdot \frac{1}{100} \, dx \, dy \\ &= 10 \int_{10}^{20} dy \int_{y}^{20} y \, dx + 5 \int_{10}^{20} dy \int_{10}^{y} (x + y) \, dx \\ &= 10 \int_{10}^{20} y(20 - y) \, dy + 5 \int_{10}^{20} \left( \frac{3}{2} y^2 - 10 y - 50 \right) dy \\ &= \frac{20000}{3} + 5 \times 1500 \approx 14166.67 \quad (\text{元}). \end{align*}

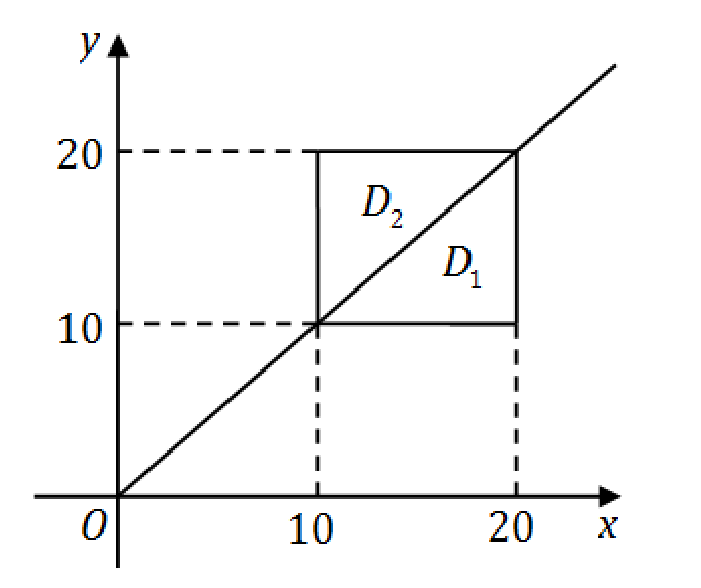
20

设有来自三个地区的各 $10$ 名、 $15$ 名和 $25$ 名考生的报名表，其中女生的报名表分别为 $3$ 份、 $7$ 份和 $5$ 份．随机地取一个地区的报名表，从中先后抽出两份．

(1) 求先抽到的一份是女生表的概率 $p$ ；

(2) 已知后抽到的一份是男生表，求先抽到的一份是女生表的概率 $q$ ．

概率论与数理统计随机事件和概率

【答案】
(1) $p = \frac{29}{90}$
(2) $q = \frac{20}{61}$

【解析】
记事件 $B_j =$ “第 $j$ 次抽到的报名表是女生表” $(j=1,2)$ ， $A_i =$ “报名表是第 $i$ 个地区的” $(i=1,2,3)$ 。易见 $A_1, A_2, A_3$ 构成一个完备事件组，且

P(A_i) = \frac{1}{3} \quad (i=1,2,3),

P(B_1|A_1) = \frac{3}{10}, \quad P(B_1|A_2) = \frac{7}{15}, \quad P(B_1|A_3) = \frac{5}{25}.

(Ⅰ) 应用全概率公式得

p = P(B_1) = \sum_{i=1}^{3} P(A_i) \cdot P(B_1|A_i) = \frac{1}{3} \left( \frac{3}{10} + \frac{7}{15} + \frac{5}{25} \right) = \frac{29}{90}.

(Ⅱ) 对事件 $B_1, B_2$ 再次用全概率公式得

P(B_1, B_2) = \sum_{i=1}^{3} P(A_i) \cdot P(B_1, B_2 | A_i) = \frac{1}{3} \left( \frac{3}{10} \cdot \frac{7}{9} + \frac{7}{15} \cdot \frac{8}{14} + \frac{5}{25} \cdot \frac{20}{24} \right) = \frac{20}{90}.

由抽签原理可知

P(B_2) = P(B_1) = \frac{61}{90},

从而

q = P(B_1|B_2) = \frac{P(B_1, B_2)}{P(B_2)} = \frac{20}{90} \cdot \frac{90}{61} = \frac{20}{61}.