卷 1
填空题
本题共5个小题,每小题3分,满分15分
1
limx→0(x21−xtanx1)=
______.
【答案】
31
【解析】
考虑极限
limx→0(x21−xtanx1)
。首先,将表达式重写为:
x21−xtanx1=x21−xsinxcosx
合并分式,公共分母为
x2sinx
:
x2sinxsinx−xcosx
因此,原极限化为:
x→0limx2sinxsinx−xcosx
使用泰勒展开:
sinx=x−6x3+O(x5)
,
cosx=1−2x2+O(x4)
。代入分子:
sinx−xcosx=(x−6x3)−x(1−2x2)=x−6x3−x+2x3=31x3+O(x5)
分母:
x2sinx=x2(x−6x3+O(x5))=x3+O(x5)
所以:
x2sinxsinx−xcosx=x3+O(x5)31x3+O(x5)=1+O(x2)31+O(x2)→31当x→0
因此,极限为
31
。
2
dxd∫0xsin((x−t)2)dt=
______.
【答案】
sin(x2)
【解析】
考虑积分
∫0xsin((x−t)2)dt
。令
u=x−t
,则当
t=0
时,
u=x
;当
t=x
时,
u=0
。且
du=−dt
,即
dt=−du
。代入积分得:
∫0xsin((x−t)2)dt=∫x0sin(u2)(−du)=∫0xsin(u2)du.
因此,原积分化为
∫0xsin(u2)du
。由微积分基本定理,对该积分求导得:
dxd∫0xsin(u2)du=sin(x2).
故原导数为
sin(x2)
。
3
微分方程
y′′−4y=e2x
的通解为
y=
______.
【答案】
y=C1e2x+C2e−2x+41xe2x
【解析】
给定微分方程
y′′−4y=e2x
,首先求解齐次方程
y′′−4y=0
。特征方程为
r2−4=0
,解得
r=±2
,因此齐次解为
yh=C1e2x+C2e−2x
。
由于非齐次项
e2x
是齐次解的一部分,设特解为
yp=Axe2x
。计算导数:
yp′=Ae2x(1+2x)
,
yp′′=4Ae2x(1+x)
。代入原方程得
4Ae2x(1+x)−4Axe2x=4Ae2x=e2x
,解得
A=41
,因此特解为
yp=41xe2x
。
通解为齐次解与特解之和,即
y=yh+yp=C1e2x+C2e−2x+41xe2x
。
4
设
n
阶矩阵
A
的元素全为
1
,则
A
的
n
个特征值是 ______.
【答案】
n
和
0
(其中
0
的重数为
n−1
)
【解析】
矩阵
A
是一个
n×n
矩阵,所有元素均为 1。由于所有行相同,矩阵的秩为 1。对于秩为 1 的矩阵,有且仅有一个非零特征值,其余特征值均为 0。
考虑向量
v=(1,1,…,1)T
,计算
Av
:
Av=11⋮111⋮1⋯⋯⋱⋯11⋮111⋮1=nn⋮n=nv 因此,
v
是特征向量,对应特征值为
n
。
对于任何与
v
正交的向量
x
,有
vTx=0
,则
Ax=vvTx=v⋅0=0
,即
Ax=0x
,因此特征值为 0。由于正交补的维数为
n−1
,故有
n−1
个特征值为 0。
综上,
A
的
n
个特征值为
n
和
0
(重数
n−1
)。
5
设两两相互独立的三事件
A
,
B
和
C
满足条件:
ABC=∅,P(A)=P(B)=P(C)<21,P(A∪B∪C)=169,
则
P(A)=
______.
【答案】
41
【解析】
设
P(A)=P(B)=P(C)=p
,其中
p<21
。由于事件
A,B,C
两两独立,且
ABC=∅
,即
P(A∩B∩C)=0
,则并集概率公式为:
P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C).
代入两两独立条件
P(A∩B)=P(A)P(B)=p2
,同理
P(A∩C)=p2
,
P(B∩C)=p2
,以及
P(A∩B∩C)=0
,得:
P(A∪B∪C)=3p−3p2.
已知
P(A∪B∪C)=169
,所以:
3p−3p2=169.
两边除以 3:
p−p2=163.
整理为二次方程:
p2−p+163=0.
乘以 16 消去分母:
16p2−16p+3=0.
解二次方程,判别式
D=(−16)2−4×16×3=256−192=64
,则:
得
p=3224=43
或
p=328=41
。由于
p<21
,故
p=41
。验证:当
p=41
时,
P(A∪B∪C)=3×41−3×(41)2=43−163=1612−163=169
,满足条件。因此
P(A)=41
。
选择题
本题共5小题,每小题3分,满分15分
6
设
f(x)
是连续函数,
F(x)
是
f(x)
的原函数,则
正确答案:A【解析】
f(x)
的原函数
F(x)
可以表示为
F(x)=∫0xf(t)dt+C
,于是
F(−x)=∫0−xf(t)dt+C=∫0xf(−u)d(−u)+C
当
f(x)
为奇函数时,
f(−u)=−f(u)
,从而有
F(−x)=∫0xf(u)du+C=∫0xf(t)dt+C=F(x)
即
F(x)
为偶函数。故 (A) 为正确选项。(B)、(C)、(D) 可分别举反例如下:
- f(x)=x2
是偶函数,但其原函数
F(x)=31x3+1
不是奇函数,可排除 (B);
- f(x)=cos2x
是周期函数,但其原函数
F(x)=21x+41sin2x
不是周期函数,可排除 (C);
- f(x)=x
在区间
(−∞,+∞)
内是单调增函数,但其原函数
F(x)=21x2
在区间
(−∞,+∞)
内非单调增函数,可排除 (D)。
7
设
f(x)={x1−cosx,x2g(x),x>0,x≤0,
其中
g(x)
是有界函数,则
f(x)
在
x=0
处
正确答案:D【解析】
首先,考虑
f(x)
在
x=0
处的极限。
- 当
x→0+
时,
f(x)=x1−cosx
。利用等价无穷小
1−cosx∼2x2
,可得
x1−cosx∼2xx2=2x3/2→0. - 当
x→0−
时,
f(x)=x2g(x)
。由于
g(x)
有界,存在
M>0
使得
∣g(x)∣≤M
,于是
∣x2g(x)∣≤x2M→0.
左右极限均为 0,且
f(0)=02⋅g(0)=0
,因此函数在
x=0
处连续。
其次,检查可导性。
- 右导数为
f+′(0)=limh→0+hf(h)−f(0)=limh→0+h3/21−cosh∼limh→0+2h1/2=0. - 左导数为
f−′(0)=limh→0−hf(h)−f(0)=limh→0−hg(h).
由于
g(h)
有界,有
∣hg(h)∣≤∣h∣M→0
,故左导数为 0。
左右导数相等,因此函数在
x=0
处可导。
8
设
f(x)={x,2−2x,0≤x≤2121<x<1
,
S(x)=2a0+∑n=1∞ancosnπx
,
−∞<x<+∞
,其中
an=2∫01f(x)cosnπxdx
(
n=0,1,2,⋯
),
则
S(−25)
等于
正确答案:C【解析】
应选 (C)。由题设知,应先将
f(x)
从 [0,1] 作偶延拓,使之成为区间 [-1,1] 上的偶函数,然后再作周期为 2 的周期延拓,再展开为傅里叶级数。因此
S(−25)=S(−2−21)=S(−21)=S(21)
而
x=21
是
f(x)
的间断点,按狄利克雷定理有
S(21)=2f(21)+f(21+)=221+1=43
9
设
A
是
m×n
矩阵,
B
是
n×m
矩阵,则
正确答案:B
【解析】 设A是m×n矩阵,B是n×m矩阵,则AB是m×m方阵。当m>n时,由于rank(A) ≤ n和rank(B) ≤ n,因此rank(AB) ≤ min(rank(A), rank(B)) ≤ n < m。这意味着AB的秩小于其阶数m,故AB是奇异矩阵,行列式|AB| = 0。因此选项B正确。当n>m时,rank(AB) ≤ m,但可能等于m,故|AB|可能不为零,也可能为零,因此选项C和D均错误。选项A与上述结论矛盾,故错误。
10
设两个相互独立的随机变量
X
和
Y
分别服从正态分布
N(0,1)
和
N(1,1)
,则
正确答案:B【解析】
根据正态分布的性质:服从正态分布的独立随机变量的线性组合仍服从正态分布。因
X
和
Y
相互独立,且
X∼N(0,1)
,
Y∼N(1,1)
,所以
X+Y∼N(1,2),X−Y∼N(−1,2).
将它们标准化得到
2X+Y−1∼N(0,1),2X−Y+1∼N(0,1). 则根据标准正态分布的对称性有
P{X+Y≤0}=P{2X+Y−1≤−21}<21, P{X+Y≤1}=P{2X+Y−1≤0}=21, P{X−Y≤0}=P{2X−Y+1≤21}>21, P{X−Y≤1}=P{2X−Y+1≤22}>21. 解答题
11
设
y=y(x)
,
z=z(x)
是由方程
z=xf(x+y)
和
F(x,y,z)=0
所确定的函数,
其中
f
和
F
分别具有一阶连续导数和一阶连续偏导数,求
dxdz
.
【答案】
dxdz=Fy+xf′(x+y)Fzf(x+y)Fy+xf′(x+y)(Fy−Fx)
其中
Fx,Fy,Fz
分别表示
F(x,y,z)
对
x,y,z
的偏导数。
【解析】
给定方程
z=xf(x+y)
和
F(x,y,z)=0
,其中
y=y(x)
和
z=z(x)
是由这两个方程确定的函数,
f
具有一阶连续导数,
F
具有一阶连续偏导数。
首先,对方程
z=xf(x+y)
两边关于
x
求导,注意
y
是
x
的函数:
dxdz=f(x+y)+xf′(x+y)(1+dxdy)
整理得:
dxdz−xf′(x+y)dxdy=f(x+y)+xf′(x+y)(1)
其次,对方程
F(x,y,z)=0
两边关于
x
求导,注意
y
和
z
是
x
的函数:
∂x∂F+∂y∂Fdxdy+∂z∂Fdxdz=0
记
Fx=∂x∂F
,
Fy=∂y∂F
,
Fz=∂z∂F
,则:
Fx+Fydxdy+Fzdxdz=0(2)
现在,方程组 (1) 和 (2) 关于
dxdy
和
dxdz
线性:
{dxdz−xf′dxdy=f+xf′Fzdxdz+Fydxdy=−Fx
其中
f=f(x+y)
,
f′=f′(x+y)
。
使用克莱姆法则求解
dxdz
。系数矩阵行列式为:
Δ=1Fz−xf′Fy=Fy+xf′Fz 替换第一列为常数项后的行列式:
Δ1=f+xf′−Fx−xf′Fy=(f+xf′)Fy−xf′Fx=fFy+xf′(Fy−Fx) 因此,
dxdz=ΔΔ1=Fy+xf′FzfFy+xf′(Fy−Fx)
即所求结果。
12
求
I=∫L(exsiny−b(x+y))dx+(excosy−ax)dy
,
其中
a
,
b
为正常数,
L
为从点
A(2a,0)
沿曲线
y=2ax−x2
到点
O(0,0)
的弧.
【答案】
I=2a2[(4+π)b−πa]
【解析】
首先,注意到被积函数中的
exsiny
和
excosy
部分与函数
U(x,y)=exsiny
的全微分有关,即
dU=exsinydx+excosydy
。因此,积分可重写为:
I=∫LdU−∫L[b(x+y)dx+axdy]=[U(O)−U(A)]−∫L[b(x+y)dx+axdy].
由于
U(O)=e0sin0=0
和
U(A)=e2asin0=0
,有
U(O)−U(A)=0
,所以:
I=−∫L[b(x+y)dx+axdy]=−b∫L(x+y)dx−a∫Lxdy.
接下来,计算积分
∫L(x+y)dx
和
∫Lxdy
。曲线
L
是从
A(2a,0)
到
O(0,0)
沿上半圆
y=2ax−x2
,即
(x−a)2+y2=a2
(
y≥0
)。考虑封闭曲线
C
由
L
和从
O
到
A
沿
x
轴的线段
L1
组成,方向为逆时针。
对于
∫L(x+y)dx
,令
P=x+y
,
Q=0
,则:
∂x∂Q−∂y∂P=0−1=−1.
由格林定理:
∮C(x+y)dx=∬D(−1)dA=−面积(D)=−21πa2.
又:
∮C(x+y)dx=∫L(x+y)dx+∫L1(x+y)dx.
在
L1
上,
y=0
,从
x=0
到
x=2a
,有:
∫L1(x+y)dx=∫02axdx=[2x2]02a=2a2.
所以:
∫L(x+y)dx=∮C(x+y)dx−∫L1(x+y)dx=−2πa2−2a2.
对于
∫Lxdy
,令
P=0
,
Q=x
,则:
∂x∂Q−∂y∂P=1−0=1.
由格林定理:
∮Cxdy=∬D1dA=面积(D)=21πa2.
又:
∮Cxdy=∫Lxdy+∫L1xdy.
在
L1
上,
y=0
,
dy=0
,所以
∫L1xdy=0
,因此:
∫Lxdy=∮Cxdy=2πa2.
代入
I
:
I=−b(−2πa2−2a2)−a(2πa2)=b(2πa2+2a2)−2πa3=2πa2b+2a2b−2πa3=2a2b+2πa2(b−a).
整理得:
I=2a2[(4+π)b−πa].
13
设函数
y(x)
(
x≥0
)二阶可导,且
y′(x)>0
,
y(0)=1
.
过曲线
y=y(x)
上任意一点
P(x,y)
作该曲线的切线及
x
轴的垂线,
上述两直线与
x
轴所围成的三角形的面积记为
S1
,区间
[0,x]
上以
y=y(x)
为曲边的曲边梯形面积记为
S2
,
并设
2S1−S2
恒为
1
,求此曲线
y=y(x)
的方程.
【答案】
y=ex
【解析】
设曲线方程为
y=y(x)
,满足
y′(x)>0
,
y(0)=1
。过点
P(x,y)
作曲线的切线和
x
轴的垂线,两直线与
x
轴围成三角形,其面积记为
S1
;区间
[0,x]
上以曲线为曲边的曲边梯形面积记为
S2
。已知
2S1−S2≡1
,求曲线方程。
首先,计算
S1
。点
P
坐标为
(x,y)
,曲线在
P
处的切线斜率为
y′
,切线方程为:
Y−y=y′(X−x).
切线与
x
轴交于点
A
,令
Y=0
,得:
0−y=y′(X−x)⇒X=x−y′y.
垂线与
x
轴交于点
B=(x,0)
。三角形顶点为
A=(x−y′y,0)
,
B=(x,0)
,
P=(x,y)
。三角形底边
AB
长度为
y′y
,高为
y
,故面积为:
S1=21⋅y′y⋅y=2y′y2.
曲边梯形面积
S2
为:
S2=∫0xy(t)dt.
由条件
2S1−S2=1
,代入得:
2⋅2y′y2−∫0xy(t)dt=1⇒y′y2−∫0xy(t)dt=1.(1)
对式 (1) 关于
x
求导(记
y=y(x)
,
y′=y′(x)
):
dxd(y′y2)−y=0.
计算导数:
dxd(y′y2)=(y′)22yy′⋅y′−y2y′′=(y′)22y(y′)2−y2y′′=2y−(y′)2y2y′′.
代入得:
2y−(y′)2y2y′′−y=0⇒y−(y′)2y2y′′=0.
由于
y>0
(由
y(0)=1
和
y′>0
可知),两边乘以
y(y′)2
:
(y′)2−yy′′=0⇒y′y′′=yy′.
积分得:
ln∣y′∣=ln∣y∣+C1⇒y′=Cy,C=eC1.
由
y′=Cy
,解得:
y=AeCx.
利用初始条件
y(0)=1
,得
A=1
,故:
y=eCx.
为确定
C
,利用条件 (1) 在
x=0
处的值。当
x=0
时,
S2=0
,计算
S1
:
点
P(0,1)
,切线斜率为
y′(0)=C
,切线与
x
轴交于点
(−C1,0)
,垂线为
x=0
,三角形面积为:
S1=21⋅C1⋅1=2C1.
代入条件:
2S1−S2=C1=1⇒C=1.
因此,曲线方程为:
y=ex.
验证:
y=ex
,则
y′=ex
,
S1=2exe2x=2ex
,
2S1=ex
,
S2=∫0xetdt=ex−1
,故
2S1−S2=ex−(ex−1)=1
,满足条件。
故所求曲线方程为
y=ex
。
14
试证:当
x>0
时,
(x2−1)lnx≥(x−1)2
.
【解析】
当
x=1
时,原不等式显然成立;当
0<x<1
时,原不等式等价于
lnx≤x+1x−1
;
当
1<x<+∞
时,原不等式等价于
lnx>x+1x−1
。令
f(x)=lnx−x+1x−1
,则
f′(x)=x1−(x+1)22=x(x+1)2x2+1>0(x>0).
又因为
f(1)=0
,利用函数单调性可知当
0<x<1
时,
f(x)<0
即
lnx<x+1x−1
;
当
1<x<+∞
时,
f(x)>0
即
lnx>x+1x−1
。综上所述,当
x>0
时,总有
(x2−1)lnx≥(x−1)2.
15
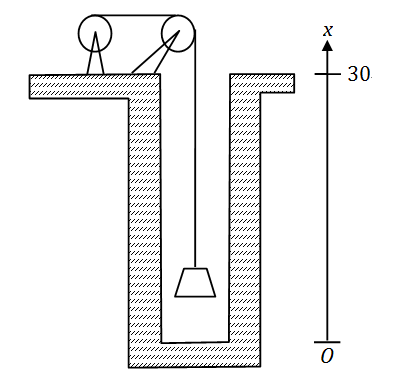
为清除井底的污泥,用缆绳将抓斗放入井底,抓起污泥后提出井口(见图),已知井深 30m,抓斗自重 400N,缆绳每米重 50N,抓斗抓起的污泥重 2000N,提升速度为
3m/s
,在提升过程中,污泥以 20N/s 的速度从抓斗缝隙中漏掉,现将抓起污泥的抓斗提升至井口,问克服重力需作多少焦耳的功?
(说明:①
1N×1m=1J
;其中
m,N,s,J
分别表示米、牛顿、秒、焦耳;
② 抓斗的高度及位于井口上方的缆绳长度忽略不计。)
【答案】
91500
【解析】
为了计算克服重力所做的功,考虑抓斗从井底(
x=0
)提升到井口(
x=30
)的过程中,井口拉力
F(x)
随高度
x
变化。功
W
为
F(x)
对
x
的积分,即
W=∫030F(x)dx
。
抓斗自重为
400N
,污泥初始重量为
2000N
,以
20N/s
的速度漏掉。提升速度为
3m/s
,因此时间
t=x/3
。污泥重量随高度变化为
2000−20⋅(x/3)=2000−320xN
。抓斗和污泥的总重量为:
G(x)=400+(2000−320x)=2400−320xN.
缆绳每米重
50N
,当抓斗在高度
x
时,井中缆绳长度为
30−x
米,重量为
50(30−x)N
。井口拉力
F(x)
需克服抓斗、污泥和井中缆绳的重力,因此:
F(x)=G(x)+50(30−x)=(2400−320x)+1500−50x=3900−3170xN.
积分求功:
W=∫030(3900−3170x)dx=[3900x−3170⋅2x2]030=[3900x−6170x2]030.
代入上下限:
W=3900×30−6170×900=117000−25500=91500J.
因此,克服重力需作
91500J
的功。
16
设
S
为椭球面
2x2+2y2+z2=1
的上半部分,
点
P(x,y,z)∈S
,
π
为
S
在点
P
处的切平面,
ρ(x,y,z)
为点
O(0,0,0)
到平面
π
的距离,
求
∬Sρ(x,y,z)zdS
.
【答案】
23π
【解析】
给定椭球面
S:2x2+2y2+z2=1
的上半部分,点
P(x,y,z)∈S
,切平面
π
的方程为
xX+yY+2zZ=2
,其中
(X,Y,Z)
为切平面上点。原点
O(0,0,0)
到切平面的距离为:
因此,被积函数为:
ρ(x,y,z)z=2zx2+y2+4z2. 曲面积分变为:
∬Sρ(x,y,z)zdS=∬S2zx2+y2+4z2dS. 参数化曲面
S
:令
x=2sinθcosϕ
,
y=2sinθsinϕ
,
z=cosθ
,其中
θ∈[0,π/2]
,
ϕ∈[0,2π]
。计算面积元素:
dS=∂θ∂r×∂ϕ∂rdθdϕ=2sinθ1+cos2θdθdϕ. 代入被积函数:
x2+y2=2sin2θ,x2+y2+4z2=2sin2θ+4cos2θ=2(1+cos2θ),
2zx2+y2+4z2=2cosθ⋅21+cos2θ=21cosθ1+cos2θ. 积分变为:
∬SρzdS=∫02π∫0π/221cosθ1+cos2θ⋅2sinθ1+cos2θdθdϕ=∫02π∫0π/2cosθsinθ(1+cos2θ)dθdϕ. 先对
ϕ
积分:
∫02πdϕ=2π,
再对
θ
积分:
2π∫0π/2cosθsinθ(1+cos2θ)dθ.
令
u=cosθ
,
du=−sinθdθ
,积分限变为
u=1
到
u=0
:
∫0π/2cosθsinθ(1+cos2θ)dθ=∫10u(1+u2)(−du)=∫01u(1+u2)du=∫01(u+u3)du=[2u2+4u4]01=21+41=43.
因此,
∬SρzdS=2π⋅43=23π.
17
设
an=∫04πtannxdx
,
(1) 求
∑n=1∞n1(an+an+2)
的值;
(2) 试证:对任意的常数
λ>0
,级数
∑n=1∞nλan
收敛.
【答案】
(1)
1
(2) 收敛
【解析】
(Ⅰ) 因为
n1(an+an+2)=n1∫04πtannx(1+tan2x)dx=n1∫04πtannxsec2xdx
=n1∫04πtannxd(tanx)=n1∫01tndt=n(n+1)1.
所以部分和数列
Sn=i=1∑ni1(ai+ai+2)=i=1∑ni(i+1)1=i=1∑n(i1−i+11)=1−n+11,
因此
n=1∑∞n1(an+an+2)=n→∞limSn=1.
(Ⅱ) 令
t=tanx
,则有
an=∫04πtannxdx=∫011+t2tn<∫01tndt=n+11⇒nλan<nλ(n+1)1<nλ+11.
由于
λ+1>0
,所以
∑n=1∞nλ+11
收敛,从而
∑n=1∞nλan
也收敛。
18
设矩阵
A=a51−c−1b0c3−a
,其行列式
∣A∣=−1
,又
A
的伴随矩阵
A∗
有一个特征值
λ0
,
属于
λ0
的一个特征向量为
α=(−1,−1,1)T
,求
a,b,c
和
λ0
的值.
【答案】
a=2
,
b=−3
,
c=2
,
λ0=1
【解析】
已知矩阵
A
的行列式
∣A∣=−1
,伴随矩阵
A∗
有一个特征值
λ0
,对应的特征向量为
α=(−1,−1,1)T
。由伴随矩阵的性质,
A∗=∣A∣A−1=−A−1
,因此
A∗α=λ0α
等价于
−A−1α=λ0α
,即
Aα=−λ01α
。令
μ=−λ01
,则
Aα=μα
。
计算
Aα
:
Aα=a51−c−1b0c3−a−1−11=−a+1+c−5−b+3−1+c−a=−a+c+1−b−2−a+c−1 而
μα=μ−1−11=−μ−μμ
,因此得到方程组:
⎩⎨⎧−a+c+1=−μ−b−2=−μ−a+c−1=μ 由第一式和第三式相减得:
(−a+c+1)−(−a+c−1)=−μ−μ⟹2=−2μ⟹μ=−1
代入第一式:
−a+c+1=−(−1)⟹−a+c+1=1⟹−a+c=0⟹a=c
代入第二式:
−b−2=−(−1)⟹−b−2=1⟹−b=3⟹b=−3
现在利用行列式
∣A∣=−1
求
a
和
c
。代入
a=c
和
b=−3
,矩阵
A
为:
计算行列式:
∣A∣=a⋅det(−303−a)−(−1)⋅det(51−a3−a)+a⋅det(51−a−30)
=a⋅[(−3)(−a)−3⋅0]+1⋅[5⋅(−a)−3⋅(1−a)]+a⋅[5⋅0−(−3)(1−a)]
=a⋅(3a)+[−5a−3+3a]+a⋅[0+3(1−a)]
=3a2+(−2a−3)+a⋅(3−3a)
=3a2−2a−3+3a−3a2
=a−3
令
∣A∣=a−3=−1
,得
a=2
,故
c=2
。
求
λ0
:由
μ=−1
和
μ=−λ01
,得
λ0=−μ1=−−11=1
。或者由伴随矩阵特征值公式,
A∗
的特征值为
μ∣A∣=−1−1=1
,故
λ0=1
。
因此,
a=2
,
b=−3
,
c=2
,
λ0=1
。
19
设
A
为
m
阶实对称矩阵且正定,
B
为
m×n
实矩阵,
BT
为
B
的转置矩阵,
试证:
BTAB
为正定矩阵的充分必要条件是
B
的秩
r(B)=n
.
【答案】
BTAB
为正定矩阵的充分必要条件是
B
的秩
r(B)=n
。
【解析】
首先,证明充分性:若
r(B)=n
,则
BTAB
正定。
由于
A
是实对称正定矩阵,且
B
列满秩,故对任意非零向量
x∈Rn
,有
Bx=0
。
于是
xT(BTAB)x=(Bx)TA(Bx)>0,
因为
A
正定且
Bx=0
。
因此
BTAB
正定。
其次,证明必要性:若
BTAB
正定,则
r(B)=n
。
假设
r(B)<n
,则存在非零向量
x∈Rn
使得
Bx=0
。
于是
xT(BTAB)x=(Bx)TA(Bx)=0,
与
BTAB
正定性矛盾。
故
r(B)=n
。
20
设随机变量
X
与
Y
相互独立,下表列出了二维随机变量
(X,Y)
的联合分布律及
关于
X
和关于
Y
的边缘分布律中的部分数值,试将其余数值填入表中的空白处.
X\Yx1x2P(Y=yj)=pjy18161y281y3P(X=xi)=pi1
【答案】
填充后的表格如下:
X\Yx1x2P(Y=yj)=pjy12418161y2818321y31214131P(X=xi)=pi41431
【解析】
由于随机变量
X
与
Y
相互独立,联合概率等于边缘概率的乘积。设
P(X=x1)=a
,
P(X=x2)=b
,则
a+b=1
。设
P(Y=y1)=61
,
P(Y=y2)=c
,
P(Y=y3)=d
,则
61+c+d=1
。
从已知条件:
P(X=x1,Y=y2)=81=a⋅c
,
P(X=x2,Y=y1)=81=b⋅61
。由后者得
b=43
,进而
a=41
。代入前者得
c=21
,于是
d=1−61−21=31
。
计算所有联合概率:
- P(X=x1,Y=y1)=a⋅P(Y=y1)=41⋅61=241
- P(X=x1,Y=y2)=81
- P(X=x1,Y=y3)=a⋅P(Y=y3)=41⋅31=121
- P(X=x2,Y=y1)=81
- P(X=x2,Y=y2)=b⋅P(Y=y2)=43⋅21=83
- P(X=x2,Y=y3)=b⋅P(Y=y3)=43⋅31=41
边缘概率:
- P(X=x1)=241+81+121=41
- P(X=x2)=81+83+41=43
- P(Y=y1)=241+81=61
- P(Y=y2)=81+83=21
- P(Y=y3)=121+41=31
所有值均一致,填入表格即可。
21
设总体
X
的概率密度为
f(x)={θ36x(θ−x),0,0<x<θ;其他.
X1,X2,⋯,Xn
是取自总体
X
的简单随机样本.
(1) 求
θ
的矩估计量
θ
;
(2) 求
θ
的方差
D(θ)
.
【答案】
(1)
θ=2Xˉ
,其中
Xˉ=n1∑i=1nXi
(2)
D(θ)=5nθ2
【解析】
首先,求总体
X
的期望
E(X)
。
计算:
E(X)=∫0θx⋅θ36x(θ−x)dx=θ36∫0θx2(θ−x)dx
积分:
∫0θx2(θ−x)dx=∫0θ(θx2−x3)dx=[θ⋅3x3−4x4]0θ=3θ4−4θ4=12θ4
所以,
E(X)=θ36⋅12θ4=2θ
根据矩估计法,令样本均值
Xˉ
等于总体期望
E(X)
,即:
Xˉ=2θ
解得矩估计量:
其次,求
θ
的方差
D(θ)
。
由于
θ=2Xˉ
,有:
其中
D(Xˉ)=nD(X)
,需先求总体方差
D(X)
。
计算
E(X2)
:
E(X2)=∫0θx2⋅θ36x(θ−x)dx=θ36∫0θx3(θ−x)dx
积分:
∫0θx3(θ−x)dx=∫0θ(θx3−x4)dx=[θ⋅4x4−5x5]0θ=4θ5−5θ5=20θ5
所以,
E(X2)=θ36⋅20θ5=103θ2
方差:
D(X)=E(X2)−[E(X)]2=103θ2−(2θ)2=103θ2−4θ2=206θ2−205θ2=20θ2
因此,
D(Xˉ)=nD(X)=20nθ2
最终,