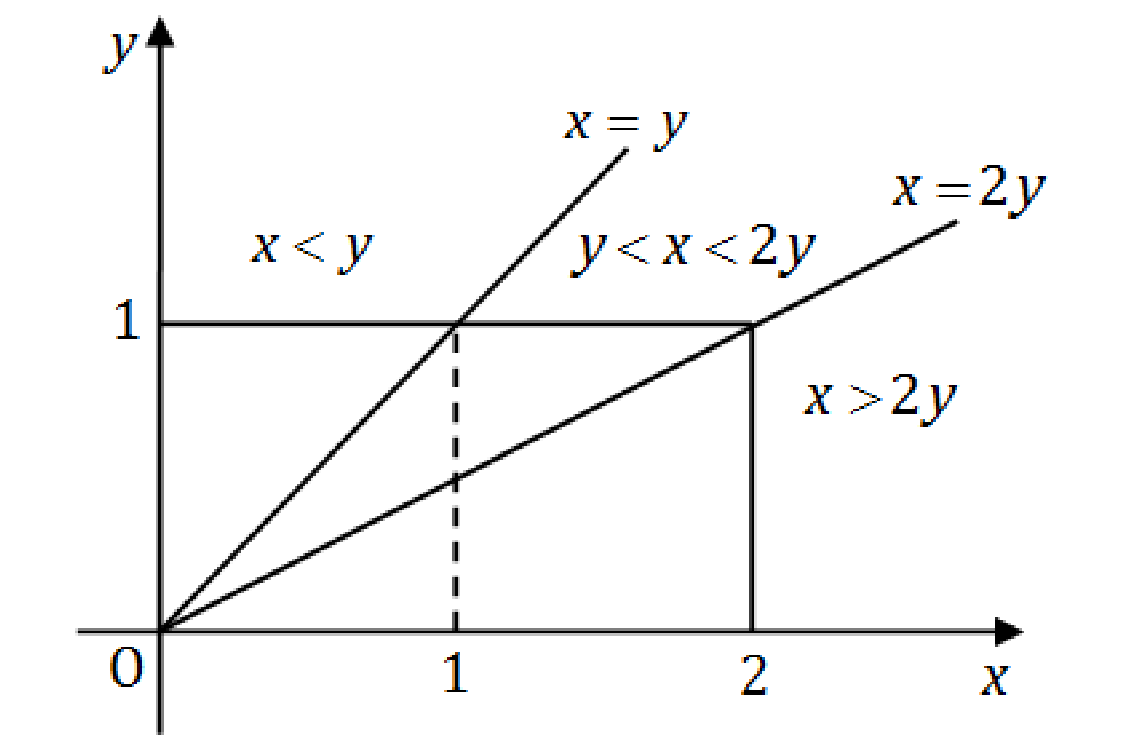卷 3
填空题
本题共5小题,每小题3分,满分15分
1
设
f(x)
有一个原函数
xsinx
,则
∫2ππxf′(x)dx=
______.
【答案】
π4−1
【解析】
已知
f(x)
有一个原函数
xsinx
,即
∫f(x)dx=xsinx+C
,因此
f(x)=dxd(xsinx)=x2xcosx−sinx
。
需要计算
∫2ππxf′(x)dx
。使用分部积分法,令
u=x
,
dv=f′(x)dx
,则
du=dx
,
v=f(x)
,于是:
∫xf′(x)dx=xf(x)−∫f(x)dx=xf(x)−xsinx+C
代入
f(x)
,有
xf(x)=x⋅x2xcosx−sinx=xxcosx−sinx=cosx−xsinx
,
所以:
∫xf′(x)dx=(cosx−xsinx)−xsinx=cosx−2xsinx+C
因此,定积分为:
∫2ππxf′(x)dx=[cosx−2xsinx]2ππ
计算上下限:
当
x=π
时,
cosπ=−1
,
sinπ=0
,所以值为
−1−2⋅π0=−1
;
当
x=2π
时,
cos2π=0
,
sin2π=1
,所以值为
0−2⋅2π1=−π4
;
于是积分值为:
−1−(−π4)=π4−1
故答案为
π4−1
。
2
∑n=1∞n(21)n−1=
______.
【答案】
4
【解析】
考虑级数
∑n=1∞nxn−1
,其中
∣x∣<1
。该级数的和为
(1−x)21
。
本题中,
x=21
,代入公式得:
n=1∑∞n(21)n−1=(1−21)21=(21)21=411=4.
因此,该级数的和为 4。
3
设
A=101020101
,而
n≥2
为整数,则
An−2An−1=
______.
【答案】
000000000
【解析】
应填
O
。因为
A2=101020101101020101=202040202=2101020101=2A, 故有
An−2An−1=An−2(A2−2A)=O.
4
在天平上重复称量一重为
a
的物品,假设各次称量结果相互独立且同服从正态分布
N(a,0.22)
.
若以
Xn
表示
n
次称量结果的算术平均值,则为使
n
的最小值应不小于自然数 ______.
【答案】
16
【解析】
由题设知
U=0.2/nXn−a∼N(0,1)
,所以
P{∣Xn−a∣<0.1}⟺P{0.2/nXn−a<0.2/n0.1}⟺P{∣U∣<2n}≥0.95≥0.95≥0.95. 查标准正态分布表知
P{∣U∣<1.96}≥0.95
。所以
2n≥1.96
,解得
n≥15.3664
。因
n
为整数,所以
n
最小为 16。
5
设随机变量
Xij(i,j=1,2,⋯,n;n≥2)
独立同分布,
EXij=2
,
则行列式
Y=X11X21⋮Xn1X12X22⋮Xn2⋯⋯⋯X1nX2n⋮Xnn
的数学期望
EY=
______.
【答案】
0
【解析】
应填
EY=0
。行列式每一项都是
n
个元素的乘积
X1j1X2j2⋯Xnjn
,前面带有正号或负号。由于随机变量
Xij(i,j=1,2,⋯,n)
相互独立,所以有
E(X1j1X2j2⋯Xnjn)=EX1j1EX2j2⋯EXnjn.
所以前面无论取正号或者负号,对和式的期望等于各项期望之和。即有
EY=EX11EX21⋮EXn1EX12EX22⋮EXn2⋯⋯⋯EX1nEX2n⋮EXnn 而
Xij(i,j=1,2,⋯,n;n⩾2)
同分布,且
EXij=2
,所以
EY=EX11EX21⋮EXn1EX12EX22⋮EXn2⋯⋯⋯EX1nEX2n⋮EXnn=22⋮222⋮2⋯⋯⋯22⋮2=0. 选择题
本题共5小题,每小题3分,满分15分
6
同试卷 1 第 6 题
7
设
f(x,y)
连续,且
f(x,y)=xy+∬Df(u,v)dudv
,
其中
D
是由
y=0
,
y=x2
,
x=1
所围成的区域,则
f(x,y)
等于
正确答案:C因为
∬Df(u,v)dudv
为一确定的数,不妨设
∬Df(u,v)dudv=a,
则
f(x,y)=xy+a
,两边同时积分得
a=∬Df(x,y)dxdy=∬D(xy+a)dxdy=∫01dx∫0x2(xy+a)dy=∫01(2x5+ax2)dx=121+3a.
解之得
a=81
,所以
f(x,y)=xy+81
,故应选 (C)。
8
设向量
β
可由向量组
α1,α2,⋯,αm
线性表示,
但不能由向量组(I)
α1,α2,⋯,αm−1
线性表示,
记向量组(II)
α1,α2,⋯,αm−1,β
,则
正确答案:B假设
αm
能由
α1,α2,⋯,αm−1
线性表示,则
β
也能由
α1,α2,⋯,αm−1
线性表示,与题设矛盾,故
αm
不能由 (I) 线性表示,从而排除 (C) 和 (D)。
由于
β
可由向量组
α1,α2,⋯,αm
线性表示,即存在常数
k1,k2,⋯,km
使得
β=k1α1+k2α2+⋯+kmαm.
而
β
不能由
α1,α2,⋯,αm−1
线性表示,从而知
km=0
。因此上式可变为
αm=km1(β−k1α1−k2α2−⋯−km−1αm−1),
即
αm
能由 (II) 线性表示,从而排除 (A) 和 (D)。故应选 (B)。
9
设
A,B
为
n
阶矩阵,且
A
与
B
相似,
E
为
n
阶单位矩阵,则
正确答案:DA
相似于
B
,则存在可逆阵
P
,使得
P−1AP=B
。因此
P−1(tE−A)P=P−1tEP−P−1AP=tE−B.
根据矩阵相似的定义,则
tE−A
相似于
tE−B
,故应选 (D)。选项 (A) 不成立:若
λE−A=λE−B
,则
A=B
,但两者未必相等。选项 (B) 不成立:
A
与
B
相似,则有相同的特征值,但未必有相同的特征向量。选项 (C) 不成立:
A
与
B
相似,但它们本身未必都相似于对角阵。
10
设随机变量
Xi∼(−141021141)(i=1,2)
,且满足
P{X1X2=0}=1
,
则
P{X1=X2}
等于
正确答案:A由题设有
P{X1X2=0}=1−P{X1X2=0}=1−1=0
。从而
P{X1X2=0}=P{X1=−1,X2=−1}+P{X1=−1,X2=1}+P{X1=1,X2=−1}+P{X1=1,X2=1}=0.
根据概率的非负性有
P{X1=−1,X2=−1}=P{X1=−1,X2=1}=P{X1=1,X2=−1}=P{X1=1,X2=1}=0.
根据边缘概率的定义有
P{X1=−1,X2=0}=P{X1=−1}−P{X1=−1,X2=−1}−P{X1=−1,X2=1}=41−0−0=41.
同理可得
P{X1=0,X2=−1}=P{X1=0,X2=1}=P{X1=1,X2=0}=P{X1=−1,X2=0}=41.
再根据边缘概率的定义有
P{X1=0,X2=0}=P{X1=0}−P{X1=0,X2=−1}−P{X1=0,X2=1}=21−41−41=0.
从而可求得
P{X1=X2}=P{X1=−1,X2=−1}+P{X1=0,X2=0}+P{X1=1,X2=1}=0+0+0=0.
解答题
11
曲线
y=x1
的切线与
x
轴和
y
轴围成一个图形,记切点的横坐标为
a
,
试求切线方程和这个图形的面积,当切点沿曲线趋于无穷远时,该面积的变换趋势如何?
【答案】
切线方程为
y=−2a3/21x+2a3
,围成的图形面积为
S=49a
。当切点沿曲线趋于无穷远时(即
a→∞
),面积
S→∞
。
【解析】
曲线
y=x1
在点
(a,a1)
处的导数为
y′=−21x−3/2,
所以在
x=a
处的切线斜率为
m=−21a−3/2.
切线方程为
化简得
切线与
x
轴的交点令
y=0
,解得
x=3a;
与
y
轴的交点令
x=0
,解得
切线与两轴围成的图形为直角三角形,其面积为
当切点沿曲线趋于无穷远时,即
a→∞
,面积
如果切点沿曲线向
y
轴方向移动(
a→0+
),则面积
S→0
,但问题中“趋于无穷远”通常指
a→∞
,故面积趋于无穷大。
12
计算二重积分
∬Dydxdy
,其中
D
是由直线
x=−2,y=0,y=2
以及曲线
x=−2y−y2
所围成的平面区域.
【答案】
4−2π
【解析】
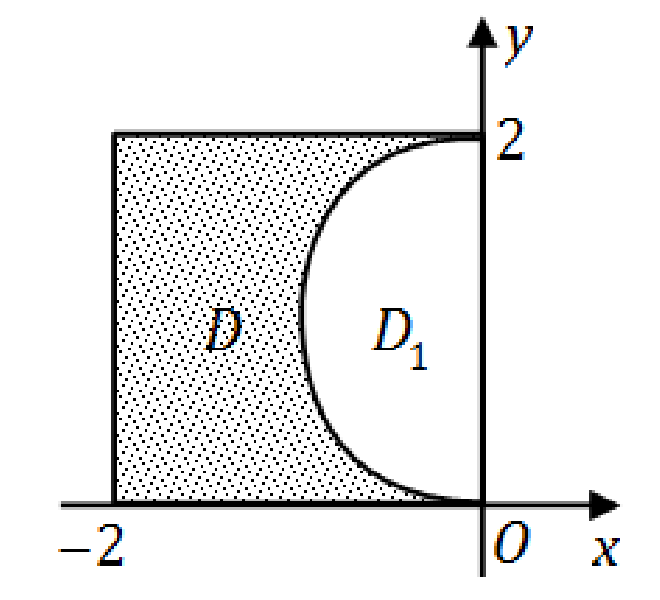
区域
D
和
D1
如图所示,有
∬Dydxdy=∬D+D1ydxdy−∬D1ydxdy=I1−I2.
显然
I1=∬D+D1ydxdy=∫−20dx∫02ydy=4
。在极坐标系下,有
D1={(r,θ)∣0≤r≤2sinθ,π/2≤θ≤π}.
因此
I2=∬D1ydxdy=∫π/2πdθ∫02sinθrsinθ⋅rdr
=38∫π/2πsin4θdθ=3×48∫π/2π[1−2cos2θ+21+cos4θ]dθ=2π.
于是
∬Dydxdy=I1−I2=4−2π.
13
设生产某种产品必须投入两种要素,
x1
和
x2
分别为两要素的投入量,
Q
为产出量;
若生产函数为
Q=2x1αx2β
,其中
α,β
为正常数,且
α+β=1
.
假设两种要素的价格分别为
p1
和
p2
,试问:当产出量为
12
时,两要素各投入多少可以使得投入总费用最小?
【答案】
当产出量为
12
时,两要素的投入量分别为:
x1=6(p1βp2α)β
x2=6(p2αp1β)α
其中
α
和
β
为正常数,且
α+β=1
,
p1
和
p2
分别为两要素的价格。
【解析】
这是一个约束优化问题,目标是在产出量
Q=12
的约束下最小化总费用
C=p1x1+p2x2
。生产函数为
Q=2x1αx2β
,且
α+β=1
。
由约束
Q=12
可得
2x1αx2β=12
,即
x1αx2β=6
。
构造拉格朗日函数:
L=p1x1+p2x2+λ(12−2x1αx2β)
取一阶偏导数并设为零:
∂x1∂L=p1−λ⋅2αx1α−1x2β=0
∂x2∂L=p2−λ⋅2βx1αx2β−1=0
∂λ∂L=12−2x1αx2β=0
从前两个方程消去
λ
,可得:
p2p1=βα⋅x1x2
即
x1x2=p2p1⋅αβ
令
k=p2αp1β
,则
x2=kx1
。代入约束
x1αx2β=6
:
x1α(kx1)β=x1kβ=6
解得
x1=6k−β=6(p1βp2α)β
代入
x2=kx1
:
x2=k⋅6k−β=6k1−β=6kα=6(p2αp1β)α
因此,当产出量为
12
时,两要素投入如上所示可使总费用最小。
14
设有微分方程
y′−2y=φ(x)
,其中
φ(x)={2,0,x<1;x>1.
试求在
(−∞,+∞)
内的连续函数
y=y(x)
,
使之在
(−∞,1)
和
(1,+∞)
内都满足所给方程,且满足条件
y(0)=0
.
【答案】
y(x)={e2x−1,e2x−e2(x−1),x≤1x>1
且在
x=1
处连续,值为
e2−1
.
【解析】
在两个区间
(−∞,1)
和
(1,+∞)
上分别求微分方程:
{y′−2y=2,y′−2y=0,x<1x>1⇒{y=−1+C1e2x,y=C2e2x,x<1;x>1;
其中
C1,C2
为常数。由题设
y(0)=0
,其中
x<0<1
,可知
yx=0=−1+C1e2xx=0=−1+C1=0. 解得
C1=1
。所以有
{y=−1+e2x,y=C2e2x,x<1;x>1.
又因为
y=y(x)
在
(−∞,+∞)
内连续,所以
x→1−limy=x→1+limy=y(1)
,即
x→1−lim(−1+e2x)=x→1+limC2e2x=y(1).
解之得
C2=1−e−2
,
y(1)=e2−1
。故所求连续函数为
y=y(x)={e2x−1,(1−e−2)e2x,x≤1;x>1.
15
设函数
f(x)
连续,且
∫0xtf(2x−t)dt=21arctanx2
.
已知
f(1)=1
,求
∫12f(x)dx
的值.
【答案】
43
【解析】
已知积分方程
∫0xtf(2x−t)dt=21arctanx2
且
f(1)=1
。
令
u=2x−t
,则积分变为
∫x2x(2x−u)f(u)du=21arctanx2
。
定义
F(x)=∫x2x(2x−t)f(t)dt
,则
F(x)=21arctanx2
。
对
F(x)
求导,使用莱布尼茨规则:
F′(x)=−xf(x)+2∫x2xf(t)dt.
同时,
F′(x)=dxd(21arctanx2)=1+x4x.
因此,
−xf(x)+2∫x2xf(t)dt=1+x4x.
代入
x=1
和
f(1)=1
:
−1⋅1+2∫12f(t)dt=1+141=21.
解得
2∫12f(t)dt=23,∫12f(t)dt=43.
故
∫12f(x)dx=43
。
16
设函数
f(x)
在区间
[0,1]
上连续,在
(0,1)
内可导,
且
f(0)=f(1)=0,f(21)=1
.试证:
(1) 存在
η∈(21,1)
,使
f(η)=η
;
(2) 对任意实数
λ
,必存在
ξ∈(0,η)
,
使得
f′(ξ)−λ[f(ξ)−ξ]=1
.
【答案】 见解析
【解析】
(I) 设
F(x)=f(x)−x
,则
F(x)
在区间
[0,1]
上连续,在
(0,1)
内可导,且
F(21)=21>0,F(1)=−1<0.
所以由介值定理得,存在
η∈(21,1)
,使得
F(η)=f(η)−η=0
,即
f(η)=η
。
(II) 令
f′(x)−λ[f(x)−x]−1=0
,解微分方程得
f(x)=x+Ceλx⇒e−λx(f(x)−x)=C.
令
F(x)=e−λx(f(x)−x)
。因为
F(0)=e0(f(0)−0)=0,F(η)=e−λη(f(η)−η)=0,
所以由罗尔定理知,存在点
ξ∈(0,η)
,使得
F′(ξ)=0
,即
F′(ξ)=e−λξ[f′(ξ)−λ[f(ξ)−ξ]−1]=0.
从而即有
f′(ξ)−λ[f(ξ)−ξ]=1.
17
同试卷 1 第 18 题
18
设
A
为
m×n
实矩阵,
E
为
n
阶单位矩阵.已知矩阵
B=λE+ATA
,
试证:当
λ>0
时,矩阵
B
为正定矩阵.
【答案】 见解析
【解析】
要证明矩阵
B
为正定矩阵,需证对于任意非零向量
x∈Rn
,有
xTBx>0
。
考虑
B=λE+ATA
,则
xTBx=xT(λE+ATA)x=λxTEx+xTATAx.
由于
E
是单位矩阵,有
xTEx=xTx=∥x∥2
。
又
xTATAx=(Ax)T(Ax)=∥Ax∥2
,
因此
xTBx=λ∥x∥2+∥Ax∥2.
当
x=0
时,有
∥x∥2>0
,且由于
λ>0
,故
λ∥x∥2>0
。
同时,
∥Ax∥2≥0
,
所以
xTBx≥λ∥x∥2>0.
因此,对于任意非零向量
x
,有
xTBx>0
,即
B
为正定矩阵。
19
假设二维随机变量
(X,Y)
在矩形
G={(x,y)∣0≤x≤2,0≤y≤1}
上服从均匀分布.记
U={0,1,X≤Y;X>Y.V={0,1,X≤2Y;X>2Y.
(1) 求
U
和
V
的联合分布;
(2) 求
U
和
V
的相关系数
r
.
【答案】
(1)
U
和
V
的联合分布为:
U=0U=1V=04141V=1021
(2)
U
和
V
的相关系数
r=31
。
【解析】
(I) 如图,由题知
P{X⩽Y}=41
,
P{X>2Y}=21
,
P{Y<X⩽2Y}=41
。
(U,V)
有四个可能值:
(0,0),(0,1),(1,0),(1,1)
。
P{U=0,V=0}=P{X≤Y,X≤2Y}=P{X≤Y}=41,
P{U=0,V=1}=P{X≤Y,X>2Y}=P{∅}=0,
P{U=1,V=0}=P{X>Y,X≤2Y}=P{Y<X≤2Y}=41,
P{U=1,V=1}=P{X>Y,X>2Y}=P{X>2Y}=21.
(II) 由边缘概率的定义有:
P{U=0}=P{U=0,V=0}+P{U=0,V=1}=41+0=41,
P{U=1}=P{U=1,V=0}+P{U=1,V=1}=41+21=43,
P{V=0}=P{U=0,V=0}+P{U=1,V=0}=41+41=21,
P{V=1}=P{U=0,V=1}+P{U=1,V=1}=0+21=21.
而随机变量
UV
的概率分布为:
P{UV=0}=P{U=0,V=0}+P{U=0,V=1}+P{U=1,V=0}=21,
P{UV=1}=P{U=1,V=1}=21.
于是有
EU=43,EU2=43,DU=EU2−(EU)2=163;
EV=21,EV2=21,DV=EV2−(EV)2=41;
E(UV)=21,Cov(U,V)=E(UV)−EU⋅EV=81.
故
U
和
V
的相关系数
r(U,V)=DUDVCov(U,V)=43×2181=33. 20
设
X1,X2,…,X9
是来自正态总体
X
的简单随机样本,
Y1=61(X1+X2+⋯+X6)
,
Y2=31(X7+X8+X9)
,
S2=21∑i=79(Xi−Y2)2
,
Z=S2(Y1−Y2)
,证明统计量
Z
服从自由度为
2
的
t
分布.
【答案】 见解析
【解析】
设
X∼N(μ,σ2)
,则
X1,…,X9∼N(μ,σ2)
。从而
Y1=61(X1+X2+…+X6)∼N(μ,6σ2),
Y2=31(X7+X8+X9)∼N(μ,3σ2).
又由于
Y1,Y2
相互独立,且都服从正态分布,故
Y1−Y2∼N(0,2σ2)
。标准化得
由正态总体样本方差的性质得
χ2=σ22S2∼χ2(2).
由于样本方差与样本均值独立,所以
Y2
与
S2
独立。而
Y1
也与
S2
独立,故
U=σ/2Y1−Y2−0
与
σ22S2
独立。所以由
t
分布的定义有
Z=S2(Y1−Y2)=σ22S2/2σ/2Y1−Y2−0=χ2/2U∼t(2).