卷 4
填空题
本题共5小题,每小题3分,满分15分
1
设函数
f(x)=ax
(
a>0
,
a=1
),
则
limn→∞n21ln[f(1)f(2)⋯f(n)]=
______.
【答案】
21lna
【解析】
函数
f(x)=ax
,则
f(1)f(2)⋯f(n)=a1⋅a2⋯an=a1+2+⋯+n=a2n(n+1)
取自然对数,得
ln[f(1)f(2)⋯f(n)]=ln(a2n(n+1))=2n(n+1)lna
代入极限式:
n→∞limn21ln[f(1)f(2)⋯f(n)]=n→∞limn21⋅2n(n+1)lna=n→∞lim2n2n(n+1)lna=n→∞lim2nn+1lna
当
n→∞
时,
2nn+1→21
,因此极限为
21lna
。
2
设
f(x)=exyz2
,其中
z=z(x,y)
是由
x+y+z+xyz=0
确定的隐函数,
则
fx′(0,1,−1)=
______.
【答案】 1
【解析】
给定函数
f(x)=exyz2
,其中
z=z(x,y)
由方程
x+y+z+xyz=0
确定。需要求
fx′(0,1,−1)
,即
f
对
x
的偏导数在点
(0,1,−1)
处的值。
首先,求
f
对
x
的偏导数。由于
z
是
x
和
y
的函数,应用乘积法则和链式法则:
fx=∂x∂(exyz2)=y(exz2+ex⋅2z⋅∂x∂z)=yex(z2+2z∂x∂z).
在点
(0,1,−1)
处,代入
x=0
,
y=1
,
z=−1
:
fx(0,1,−1)=1⋅e0((−1)2+2(−1)∂x∂z(0,1))=1⋅1(1−2∂x∂z(0,1))=1−2∂x∂z(0,1). 接下来,求
∂x∂z
在点
(0,1)
处的值。由隐函数方程
F(x,y,z)=x+y+z+xyz=0
,利用隐函数求导公式:
∂x∂z=−∂z∂F∂x∂F.
计算偏导数:
∂x∂F=1+yz,∂z∂F=1+xy.
在点
(0,1,−1)
处:
∂x∂F=1+(1)(−1)=0,∂z∂F=1+(0)(1)=1.
所以,
代入回
fx
:
fx(0,1,−1)=1−2×0=1.
因此,
fx′(0,1,−1)=1
.
3
同试卷 3 第 3 题
4
已知
AB−B=A
,其中
B=120−210002
,则
A=
______.
【答案】
【解析】
已知矩阵方程
AB−B=A
,可改写为
AB−A=B
,即
A(B−I)=B
,其中
I
是单位矩阵。
给定
则
计算
(B−I)−1
:由于
B−I
是分块矩阵,其逆矩阵为
(B−I)−1=0−2102100001. 因此,
A=B(B−I)−1=120−2100020−2102100001=1−2102110002. 验证:计算
AB−B
,结果等于
A
,符合原方程。
5
设
X
服从参数为
λ
的泊松分布,且已知
E[(X−1)(X−2)]=1
,则
λ=
______.
【答案】 1
【解析】
已知
X
服从参数为
λ
的泊松分布,且
E[(X−1)(X−2)]=1
。
展开
(X−1)(X−2)=X2−3X+2
,则
E[(X−1)(X−2)]=E[X2−3X+2]=E[X2]−3E[X]+2.
对于泊松分布,有
E[X]=λ
,且
E[X2]=Var(X)+(E[X])2=λ+λ2
。
代入得:
E[X2−3X+2]=(λ+λ2)−3λ+2=λ2−2λ+2.
设其等于 1:
λ2−2λ+2=1,
即
λ2−2λ+1=0,
解得
(λ−1)2=0
,所以
λ=1
。
验证:当
λ=1
时,
E[X]=1
,
E[X2]=1+12=2
,则
E[X2−3X+2]=2−3×1+2=1
,符合条件。
因此,
λ=1
。
选择题
本题共5小题,每小题3分,满分15分
6
同试卷 1 第 6 题
7
同试卷 3 第 7 题
8
同试卷 3 第 8 题
9
设随机变量
X
和
Y
的方差存在且不等于
0
,则
D(X+Y)=DX+DY
是
X
和
Y
正确答案:C【解析】根据方差的性质,对于随机变量
X
和
Y
,有
D(X+Y)=DX+DY+2Cov(X,Y)
因此,
D(X+Y)=DX+DY
当且仅当
Cov(X,Y)=0
。而
Cov(X,Y)=0
正是
X
和
Y
不相关的定义。故
D(X+Y)=DX+DY
是
X
和
Y
不相关的充要条件。
选项 A、B、D 均不正确,因为不相关并不一定意味着独立,独立是更强的条件。
10
设
X
服从指数分布,则
Y=min{X,2}
的分布函数
正确答案:D【解析】
设随机变量
X
服从参数为
λ
的指数分布,其分布函数为
FX(x)=1−e−λx(x≥0).
考虑
Y=min{X,2}
的分布函数
FY(y)=P(Y≤y)
。
- 当
y<0
时,
FY(y)=0
。
- 当
0≤y<2
时,
FY(y)=P(X≤y)=1−e−λy
。
- 当
y≥2
时,
FY(y)=1
。
在
y=0
处,
FY(0)=0
,且左极限为
0
,故连续。
在
y=2
处,
FY(2)=1
,左极限为
1−e−2λ<1
,故存在跳跃间断点。
其余点处
FY(y)
连续,因此分布函数恰有一个间断点。
选项分析:
A 错误,因为分布函数不连续;
B 错误,因为只有一个间断点;
C 错误,因为并非阶梯函数(仅在
y=2
处跳跃,其余部分连续);
D 正确。
解答题
11
同试卷 3 第 11 题
12
同试卷 3 第 12 题
13
同试卷 3 第 13 题
14
设
F(x)
为
f(x)
的原函数,且当
x≥0
时,
f(x)F(x)=2(1+x)2xex
,
已知
F(0)=1
,
F(x)>0
,试求
f(x)
.
【答案】
f(x)=2(1+x)23xe2x
【解析】
已知
F(x)
是
f(x)
的原函数,即
F′(x)=f(x)
,且当
x≥0
时,有
f(x)F(x)=2(1+x)2xex,
同时给定
F(0)=1
,
F(x)>0
。
令
u=F(x)
,则
u′=f(x)
,代入得
u′u=2(1+x)2xex.
注意到左边为
21(u2)′
,因此
21(u2)′=2(1+x)2xex⇒(u2)′=(1+x)2xex.
积分两边:
u2=∫(1+x)2xexdx+C.
计算积分:
∫(1+x)2xexdx=1+xex,
因为
(1+xex)′=(1+x)2ex(1+x)−ex=(1+x)2xex.
所以
u2=1+xex+C.
由
F(0)=1
,即
u(0)=1
,代入得
1=1+0e0+C=1+C⇒C=0.
因此
u2=1+xex⇒u=1+xex=1+xe2x, 即
求导得
f(x)=F′(x)=dxd(e2x(1+x)−21).
应用乘积法则:
f(x)=e2x⋅21(1+x)−21+e2x⋅(−21)(1+x)−23=2e2x[1+x1−(1+x)231]. 化简括号内:
1+x1−(1+x)231=(1+x)23(1+x)−1=(1+x)23x, 所以
f(x)=2e2x⋅(1+x)23x=2(1+x)23xe2x.
验证:计算
f(x)F(x)
:
f(x)F(x)=2(1+x)23xe2x⋅1+xe2x=2(1+x)2xex, 符合给定条件。因此所求函数为
f(x)=2(1+x)23xe2x.
15
已知
f(x)
连续,
∫0xtf(x−t)dt=1−cosx
,求
∫02πf(x)dx
的值.
【答案】
1
【解析】
已知积分方程
∫0xtf(x−t)dt=1−cosx
,且
f(x)
连续。
令
u=x−t
,则当
t=0
时,
u=x
;当
t=x
时,
u=0
,且
dt=−du
。
代入原积分得:
∫0xtf(x−t)dt=∫x0(x−u)f(u)(−du)=∫0x(x−u)f(u)du
因此,有:
∫0x(x−u)f(u)du=1−cosx
将积分写为:
x∫0xf(u)du−∫0xuf(u)du=1−cosx
令
F(x)=∫0xf(u)du
,则上式化为:
xF(x)−∫0xuf(u)du=1−cosx
对两边关于
x
求导:
左边求导为:
dxd[xF(x)−∫0xuf(u)du]=F(x)+xf(x)−xf(x)=F(x)
右边求导为:
dxd(1−cosx)=sinx
因此,
F(x)=sinx
即
∫0xf(u)du=sinx
所求积分为:
∫02πf(x)dx=F(2π)=sin2π=1
故答案为 1。
16
证明:当
0<x<π
时,有
sin2x>πx
.
【答案】 见解析
【解析】
令
t=2x
,则当
0<x<π
时,有
0<t<2π
。原不等式化为
sint>π2t
。
考虑函数
s(t)=tsint
,其中
t>0
。求导得
s′(t)=t2tcost−sint.
令
u(t)=tcost−sint
,则
u′(t)=cost−tsint−cost=−tsint<0(当 t>0),
故
u(t)
单调递减。又
u(0)=t→0lim(tcost−sint)=0,
所以对任意
t>0
,有
u(t)<0
,因此
s′(t)<0
,即
s(t)
在
t>0
时单调递减。
当
t=2π
时,
s(2π)=2πsin2π=π2.
由于
s(t)
单调递减,当
0<t<2π
时,有
s(t)>s(2π)=π2,
即
tsint>π2,
所以
sint>π2t
。
代回
t=2x
,得
sin2x>π2⋅2x=πx.
因此,当
0<x<π
时,原不等式成立。
17
设矩阵
A=3−k42−12−2k−3
,问:当
k
为何值时,存在可逆矩阵
P
,使得
P−1AP
为对角矩阵?并求出
P
和相应的对角矩阵.
【答案】
当
k=0
时,存在可逆矩阵
P
,使得
P−1AP
为对角矩阵。
可逆矩阵
P=101102011
,相应的对角矩阵为
Λ=1000−1000−1
。
【解析】
矩阵
A
的特征多项式为
det(A−λI)=−λ3−λ2+λ+1
,即
λ3+λ2−λ−1=0
,解得特征值为
λ=1
(单根)和
λ=−1
(二重根)。
要使
A
可对角化,需要特征值
λ=−1
的几何重数等于其代数重数
2
,即
dimnull(A+I)=2
。
计算
当
k=0
时,
其秩为
1
,零空间维数为
2
,满足可对角化条件。
当
k=0
时,求解特征向量:
令可逆矩阵
P
由这些特征向量组成:
对角矩阵
Λ
由特征值构成:
验证
P
可逆:
det(P)=−1=0.
18
已知线性方程组
⎩⎨⎧x1+x2+x3=0,ax1+bx2+cx3=0,a2x1+b2x2+c2x3=0.
(1) 当
a
,
b
,
c
满足何种关系时,方程组仅有零解?
(2) 当
a
,
b
,
c
满足何种关系时,方程组有无穷多组解,并用基础解系表示全部解.
【答案】
(1) 当
a,b,c
互不相等时,方程组仅有零解。
(2) 当
a,b,c
中至少有两个相等时,方程组有无穷多解:
- 若
a=b=c
,基础解系为
1−10
,全部解为
k1−10
(
k
为任意常数)
- 若
a=c=b
,基础解系为
10−1
,全部解为
k10−1
(
k
为任意常数)
- 若
b=c=a
,基础解系为
01−1
,全部解为
k01−1
(
k
为任意常数)
- 若
a=b=c
,基础解系为
10−1
和
01−1
,全部解为
k110−1+k201−1
(
k1,k2
为任意常数)
(注:基础解系不唯一,但不同基础解系之间存在线性关系)
【解析】
线性方程组解的分析
这是一个齐次线性方程组,系数矩阵为范德蒙德矩阵:
(1) 仅有零解的条件
齐次线性方程组仅有零解的条件是系数矩阵满秩,即
rank(A)=3
。
范德蒙德矩阵的行列式为:
det(A)=(b−a)(c−a)(c−b)
当
det(A)=0
时,矩阵满秩,方程组仅有零解。
所以,当
a,b,c
互不相等时,方程组仅有零解。
(2) 有无穷多解的条件及基础解系
当
det(A)=0
时,矩阵不满秩,方程组有无穷多解。即当
a,b,c
中至少有两个相等时,方程组有无穷多解。
具体分析如下:
情况1:
a=b=c
方程组变为:
⎩⎨⎧x1+x2+x3=0,ax1+ax2+cx3=0,a2x1+a2x2+c2x3=0. 解得:
x3=0
,
x2=−x1
,所以通解为:
x1x2x3=k1−10,k∈R 基础解系:
1−10
情况2:
a=c=b
方程组变为:
⎩⎨⎧x1+x2+x3=0,ax1+bx2+ax3=0,a2x1+b2x2+a2x3=0. 解得:
x2=0
,
x3=−x1
,所以通解为:
x1x2x3=k10−1,k∈R 基础解系:
10−1
情况3:
b=c=a
方程组变为:
⎩⎨⎧x1+x2+x3=0,ax1+bx2+bx3=0,a2x1+b2x2+b2x3=0. 解得:
x1=0
,
x3=−x2
,所以通解为:
x1x2x3=k01−1,k∈R 基础解系:
01−1
情况4:
a=b=c
方程组变为:
⎩⎨⎧x1+x2+x3=0,ax1+ax2+ax3=0,a2x1+a2x2+a2x3=0. 所有方程等价于
x1+x2+x3=0
,所以通解为:
x1x2x3=k110−1+k201−1,k1,k2∈R 基础解系:
10−1
和
01−1
19
设二维随机变量
(X,Y)
在矩形
G={(x,y)∣0≤x≤2,0≤y≤1}
上服从均匀分布,
试求边长为
X
和
Y
的矩形面积
S
的概率密度
f(s)
.
【答案】
f(s)={21(ln2−lns),0,0<s<2;其他.
【解析】
二维随机变量
(X,Y)
的概率密度为
ϕ(x,y)={21,0,若 (x,y)∈G;若 (x,y)∈/G.
设
F(s)=P{S≤s}
为
S
的分布函数,则当
s≤0
时,
F(s)=0
;当
s≥2
时,
F(s)=1
。
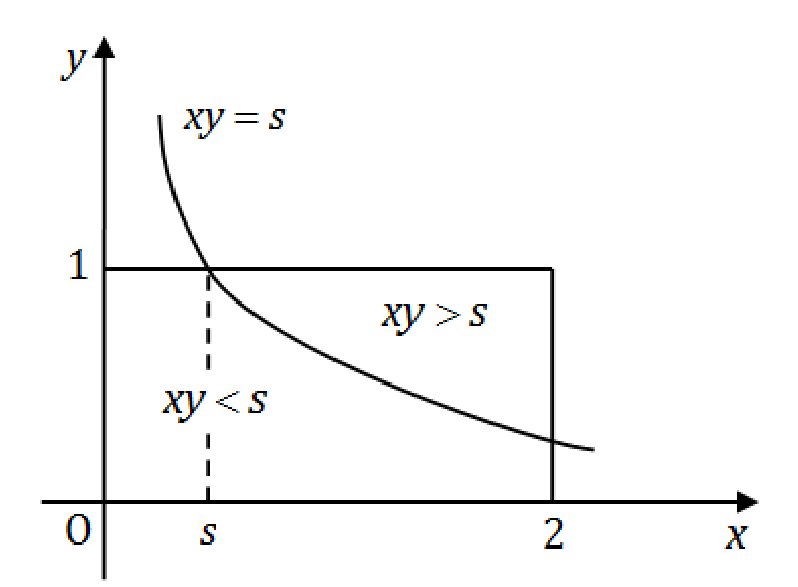
现设
0<s<2
,曲线
xy=s
与矩形
G
的上边交于点
(s,1)
,于是
F(s)=P{S≤s}=P{XY≤s}=1−P{XY>s}=1−∬xy>s21dxdy=1−21∫s2dx∫xs1dy=2s(1+ln2−lns).
因此
f(s)={21(ln2−lns),0,0<s<2;其他.
20
已知随机变量
X1
和
X2
的概率分布为
X1P−141021141,X2P021121
且
P{X1X2=0}=1
.
(1) 求
X1
和
X2
的联合分布;
(2) 问
X1
和
X2
是否独立?为什么?
【答案】
(1)
X1
和
X2
的联合分布为:
X1=−1X1=0X1=1X2=041041X2=10210
(2)
X1
和
X2
不独立。
【解析】
(1) 已知
P{X1X2=0}=1
,即
X1X2=0
的概率为 0,因此
P(X1=−1,X2=1)=0,P(X1=1,X2=1)=0
根据边缘分布:
P(X1=−1)P(X1=1)P(X2=0)P(X2=1)=41⇒P(X1=−1,X2=0)=41,=41⇒P(X1=1,X2=0)=41,=21⇒P(X1=0,X2=0)=0,=21⇒P(X1=0,X2=1)=21
因此联合分布如上表。
(2) 对于独立性,检查
P(X1=0,X2=0)=0
而
P(X1=0)P(X2=0)=21×21=41=0
故不独立。