卷 3
填空题
本题共5小题,每小题3分,满分15分
1
设
z=f(xy,yx)+g(yx)
,其中
f,g
均可微,则
∂x∂z=
______.
【答案】
∂x∂z=y∂u∂f+y1∂v∂f+y1∂v∂g
其中
u=xy
,
v=yx
. 或者使用偏导数记号:
∂x∂z=yf1+y1f2+y1g′
其中
f1
表示
f
对第一个变量的偏导数,
f2
表示
f
对第二个变量的偏导数,
g′
表示
g
对它的变量的导数。
【解析】
设
u=xy
,
v=yx
,则
z=f(u,v)+g(v)
。
求偏导数
∂x∂z
,使用链式法则:
∂x∂z=∂u∂f⋅∂x∂u+∂v∂f⋅∂x∂v+∂v∂g⋅∂x∂v
计算
∂x∂u=y
,
∂x∂v=y1
,代入得:
∂x∂z=∂u∂f⋅y+∂v∂f⋅y1+∂v∂g⋅y1=y∂u∂f+y1(∂v∂f+∂v∂g)
因此,结果为
y∂u∂f+y1∂v∂f+y1∂v∂g
。
2
∫1+∞ex+e2−xdx=
【答案】
4eπ
【解析】
考虑积分
I=∫1+∞ex+e2−xdx
。
分母可写为
ex+e2e−x
,分子分母同时乘以
ex
,得:
I=∫1+∞e2x+e2exdx
令
t=ex
,则
dt=exdx
,积分限变为:当
x=1
时
t=e
,当
x→+∞
时
t→+∞
。
于是:
I=∫e+∞t2+e2dt
该积分是标准形式,有:
∫t2+a2dt=a1arctanat+C
其中
a=e
,所以:
I=[e1arctanet]e+∞=e1(arctan(+∞)−arctan(1))=e1(2π−4π)=e1⋅4π=4eπ
因此,积分值为
4eπ
。
3
若四阶矩阵
A
与
B
相似,矩阵
A
的特征值为
21,31,41,51
,
则行列式
B−1−E=
______.
【答案】
24
【解析】
由于矩阵
A
与
B
相似,它们具有相同的特征值,即
21,31,41,51
。
设
λ
为
B
的特征值,则
B−1
的特征值为
λ−1
,进而
B−1−E
的特征值为
λ−1−1=λ1−λ
。
因此,行列式
∣B−1−E∣=∏(λ1−λ)=∏λ∏(1−λ).
计算乘积:
∏λ=21⋅31⋅41⋅51=1201,
∏(1−λ)=(1−21)(1−31)(1−41)(1−51)=21⋅32⋅43⋅54=51.
于是,
∣B−1−E∣=1/1201/5=5120=24.
故答案为 24。
4
设随机变量
X
的概率密度为
f(x)=⎩⎨⎧1/3,2/9,0,x∈[0,1];x∈[3,6];其他.
若
k
使得
P{X≥k}=32
,则
k
的取值范围是 ______.
【答案】
[1,3]
【解析】
随机变量
X
的概率密度函数
f(x)
在区间
[0,1]
上为
1/3
,在区间
[3,6]
上为
2/9
,其余区间为 0。需要求
k
使得
P{X≥k}=32
。
计算
P{X≥k}
需考虑
k
的不同取值范围:
- 当
k≤0
时,
P{X≥k}=1>32
,不满足。
- 当
k>6
时,
P{X≥k}=0<32
,不满足。
- 当
k∈[0,1]
时,
P{X≥k}=∫k131dx+∫3692dx=31(1−k)+32.
令其等于
32
,得
31(1−k)=0
,即
k=1
。
- 当
k∈(1,3)
时,
P{X≥k}=∫3692dx=32,
恒满足。
- 当
k∈[3,6]
时,
P{X≥k}=∫k692dx=92(6−k).
令其等于
32
,得
92(6−k)=32
,解得
k=3
。
综上,当
k∈[1,3]
时,
P{X≥k}=32
。因此,
k
的取值范围是
[1,3]
。
5
假设随机变量
X
在区间
[−1,2]
上服从均匀分布,随机变量
Y=⎩⎨⎧1,0,−1,若X>0;若X=0;若X<0.
则方差
D(Y)=
______.
【答案】
98
【解析】
随机变量
X
在区间
[−1,2]
上服从均匀分布,其概率密度函数为
fX(x)=31
,其中
x∈[−1,2]
。
随机变量
Y
的定义为:
Y=⎩⎨⎧1,0,−1, X>0; X=0; X<0. 由于
X
是连续随机变量,有
P(X=0)=0
,因此
P(Y=0)=0
。
计算
Y
的概率分布:
- P(Y=1)=P(X>0)=∫0231dx=32
,
- P(Y=−1)=P(X<0)=∫−1031dx=31
。
于是,
Y
的期望为:
E[Y]=1⋅32+(−1)⋅31=32−31=31.
Y2
的期望为:
E[Y2]=12⋅32+(−1)2⋅31=32+31=1.
方差为:
D(Y)=E[Y2]−(E[Y])2=1−(31)2=1−91=98.
因此,方差
D(Y)=98
。
选择题
本题共5小题,每小题3分,共15分
6
设对任意的
x
,总有
φ(x)≤f(x)≤g(x)
,且
limx→∞[g(x)−φ(x)]=0
,
则
limx→∞f(x)
正确答案:D【解析】
用排除法。首先设
x2+2x2≤f(x)≤x2+2x2+1,
满足条件
x→∞lim[x2+2x2+1−x2+2x2]=x→∞limx2+21=0,x→∞limx2+2x2+1=1,x2+2x2=1.
由夹逼准则知,
x→∞limf(x)=1,
则选项 (A) 和 (C) 错误。
其次设
x4+1x6+x2≤f(x)≤x4+1x6+2x2,
满足条件
x→∞lim[x4+1x6+2x2−x4+1x6+x2]=x→∞limx4+1x2=0.
但是由于
f(x)≥x4+1x6+x2=x2,
有
x→∞limf(x)=+∞,
极限不存在,故选项 (B) 也是错误的。
7
设函数
f(x)
在点
x=a
处可导,则函数
∣f(x)∣
在点
x=a
处不可导的充分条件是
正确答案:B【解析】
应选 (B)。这是因为由 (B) 的条件
f(a)=0
,则有
x→alimx−a∣f(x)∣−∣f(a)∣=x→alimx−a∣f(x)∣=x→alimx−a∣f(x)−f(a)∣,
所以
x→a+limx−a∣f(x)−f(a)∣=x→a+limx−af(x)−f(a)=∣f′(a)∣, x→a−limx−a∣f(x)−f(a)∣=x→a−lim(−x−af(x)−f(a))=−∣f′(a)∣. 8
设
α1,α2,α3
是四元非齐次线性方程组
AX=b
的三个解向量,
且秩
r(A)=3
,
α1=(1,2,3,4)T
,
α2+α3=(0,1,2,3)T
,
c
表示任意常数,则线性方程组
AX=b
的通解
X=
正确答案:C【解析】
已知线性方程组
AX=b
是四元方程组,且秩
r(A)=3
,因此齐次方程组
AX=0
的解空间维数为
4−3=1
,即基础解系只含一个线性无关的解向量。给定
α1=(1,2,3,4)T
是特解,通解形式为
X=α1+cη
,其中
η
是齐次方程组的基础解系。
由
α2
和
α3
都是解,设
α2=α1+c2η
,
α3=α1+c3η
,则
α2+α3=2α1+(c2+c3)η
。代入已知
α2+α3=(0,1,2,3)T
和
α1=(1,2,3,4)T
,得:
2α1+kη=(0,1,2,3)T
其中
k=c2+c3
。计算:
2α1=(2,4,6,8)T
kη=(0,1,2,3)T−(2,4,6,8)T=(−2,−3,−4,−5)T
因此
η
与
(−2,−3,−4,−5)T
成比例。取
η=(2,3,4,5)T
(忽略常数倍,因
c
为任意常数),通解为:
对应选项 C。其他选项的
η
不满足条件。
9
设
A
为
n
阶实矩阵,
AT
是
A
的转置矩阵,则对于线性方程组(Ⅰ):
AX=0
和(Ⅱ):
ATAX=0
,必有
正确答案:A【解析】
应选 (A). 若
α
是方程组 (I):
AX=0
的解,即
Aα=0
,两边左乘
AT
,得
ATAα=0
,即
α
也是方程组 (II):
ATAX=0
的解,即 (I) 的解也是 (II) 的解。
若
β
是方程组 (II):
ATAX=0
的解,即
ATAβ=0
,两边左乘
βT
得
βTATAβ=(Aβ)TAβ=0.
Aβ
是一个向量,设
Aβ=[b1,b2,⋯,bn]T
,则
(Aβ)TAβ=i=1∑nbi2=0.
故有
bi=0, i=1,2,⋯,n
。从而有
Aβ=0
,即
β
也是方程组 (I):
AX=0
的解。
10
在电炉上安装了
4
个温控器,其显示温度的误差是随机的.
在使用过程中,只要有两个温控器显示的温度不低于临界温度
t0
,电炉就断电.
以
E
表示事件“电炉断电”,而
T(1)≤T(2)≤T(3)≤T(4)
为
4
个温控器显示的按递增顺序排列的温度值,
则事件
E
等于事件
正确答案:C【解析】 事件
E
表示电炉断电,其条件是至少有两个温控器显示的温度不低于临界温度
t0
。由于温度值按递增顺序排列为
T(1)≤T(2)≤T(3)≤T(4)
,分析如下:
- 如果
T(3)≥t0
,则
T(3)
和
T(4)
均不低于
t0
,满足至少两个温控器显示温度不低于
t0
的条件,即事件
E
发生。
- 反之,如果事件
E
发生,即至少有两个温控器显示温度不低于
t0
,则
T(3)
必须不低于
t0
。因为如果
T(3)<t0
,则
T(1)≤T(2)≤T(3)<t0
,最多只有
T(4)
可能不低于
t0
,即最多只有一个温控器显示温度不低于
t0
,与事件
E
矛盾。
因此,事件
E
等价于
{T(3)≥t0}
。
对于其他选项:
- A.
{T(1)≥t0}
表示所有温控器显示温度均不低于
t0
,条件过强,不必要。
- B.
{T(2)≥t0}
表示至少三个温控器显示温度不低于
t0
,条件过强,不必要(例如当
T(2)<t0
但
T(3)≥t0
时,事件
E
仍发生)。
- D.
{T(4)≥t0}
表示至少一个温控器显示温度不低于
t0
,条件过弱,可能只有一个温控器满足条件,事件
E
不发生。
故正确答案为 C。
解答题
11
求微分方程
y′′−2y′−e2x=0
满足条件
y(0)=0,y′(0)=1
.
【答案】
y=41(e2x−1)+21xe2x
【解析】
给定微分方程
y′′−2y′−e2x=0
满足条件
y(0)=0
,
y′(0)=1
。
首先求解齐次方程
y′′−2y′=0
。特征方程为
r2−2r=0
,解得
r=0
和
r=2
,齐次解为
yh=C1+C2e2x
。
非齐次项为
e2x
,由于
e2x
是齐次解的一部分,设特解
yp=Axe2x
。计算导数:
yp′=Ae2x(1+2x),
yp′′=4Ae2x(1+x).
代入原方程:
yp′′−2yp′−e2x=4Ae2x(1+x)−2Ae2x(1+2x)−e2x=e2x(2A−1)=0,
解得
A=21
,特解为
yp=21xe2x
。
通解为
y=yh+yp=C1+C2e2x+21xe2x
。
应用初始条件:
由
y(0)=0
得
C1+C2=0
。
计算导数
y′=2C2e2x+21e2x+xe2x
,由
y′(0)=1
得
2C2+21=1
,解得
C2=41
,代入得
C1=−41
。
因此解为
y=−41+41e2x+21xe2x=41(e2x−1)+21xe2x.
12
计算二重积分
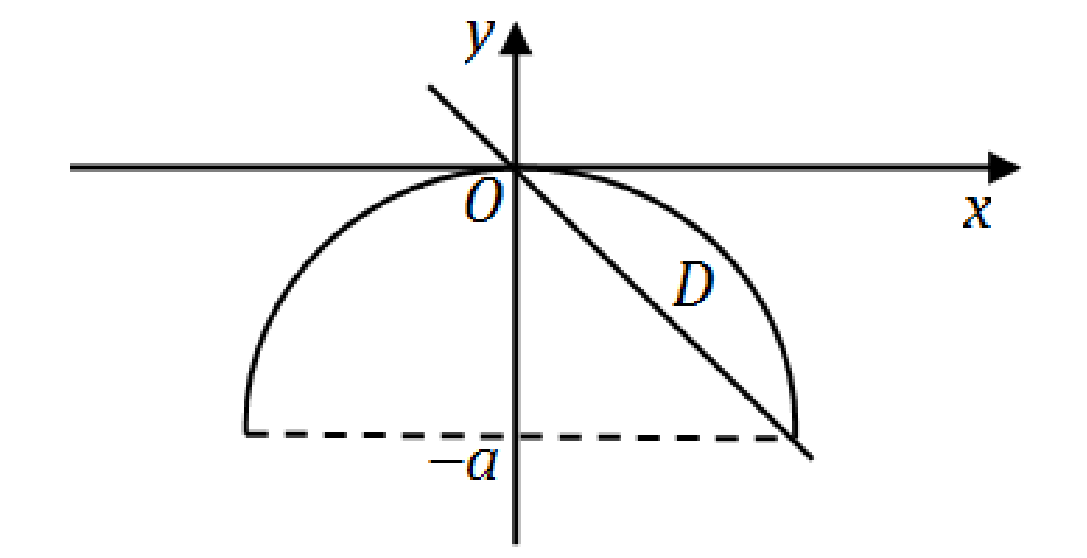
∬D4a2−x2−y2x2+y2dσ
,
其中
D
是由曲线
y=−a+a2−x2(a>0)
和直线
y=−x
围成的区域.
【答案】
a2(16π2−21)
【解析】
画出积分区域D如下图,采用极坐标更为方便:
在极坐标系下区域
D={(ρ,θ)∣−4π≤θ≤0,0≤ρ≤−2asinθ}
,则有
I=∬D4a2−x2−y2x2+y2dσ=∫−4π0dθ∫0−2asinθ4a2−ρ2ρ2dρ. 令
ρ=2asint
,则有
I=∫−4π0dθ∫0−θ4a2sin2tdt=∫−4π0dθ∫0−θ2a2(1−cos2t)dt=2a2∫−4π0(−θ+21sin2θ)dθ=a2(16π2−21).
13
假设某企业在两个相互分割的市场上出售同一种产品,两个市场的需求函数分别是
P1=18−Q1,P2=12−Q2,
其中
P1
和
P2
分别表示该产品在两个市场的价格(单位:万元/吨),
Q1
和
Q2
分别表示该产品在两个市场的销售量(即需求量,单位:吨),
并且该企业生产这种产品的总成本函数是
C=2Q+5
,其中
Q
表示该产品在两个市场的销售总量,即
Q=Q1+Q2
.
(1) 如果该企业实行价格差别策略,试确定两个市场上该产品的销售量和价格,使该企业获得最大利润;
(2) 如果该企业实行价格无差别策略,试确定两个市场上该产品的销售量及其统一的价格,
使该企业的总利润最大化;并比较两种价格策略下的总利润大小.
【答案】
(1)
Q1=4, P1=10; Q2=5, P2=7; 利润=52
万元
(2)
Q1=5, Q2=4; 利润=49
万元;差别定价利润更高。
【解析】
(I) 记总利润函数为
L
,总收益函数为
R
,则总利润
L=R−C=P1Q1+P2Q2−(2Q+5)=−2Q12−Q22+16Q1+10Q2−5.
其中,
Q1>0,Q2>0
。令
∂Q1∂L=−4Q1+16=0,∂Q2∂L=−2Q2+10=0,
解得
Q1=4,Q2=5
;相应地
P1=10,P2=7
。在
Q1>0,Q2>0
的范围内驻点唯一,且实际问题在
Q1>0,Q2>0
范围内必有最大值,故在
Q1=4,Q2=5
处有最大利润
L=−2×42−52+16×4+10×5−5=52(万元).
(II) 若两地的销售单价无差别,即
P1=P2
,于是得
2Q1−Q2=6
,在此约束条件下求
L
的最值。构造拉格朗日函数
F(Q1,Q2,λ)=−2Q12−Q22+16Q1+10Q2−5+λ(2Q1−Q2−6),
令
⎩⎨⎧∂Q1∂F=−4Q1+16+2λ=0∂Q2∂F=−2Q2+10−λ=0∂λ∂F=2Q1−Q2−6=0 解得
Q1=5,Q2=4
,在
Q1>0,Q2>0
的范围内驻点唯一,且实际问题在
Q1>0,Q2>0
范围内必有最大值,故在
Q1=5,Q2=4
处有最大利润
L=−2×52−42+16×5+10×4−5=49(万元).
14
求函数
y=(x−1)e2π+arctanx
的单调区间和极值,并求该函数图形的渐近线.
【答案】 见解析
【解析】
对
x
求导得
y′=x2+1x2+xe2π+arctanx
。令
y′=0
,得驻点
x1=0,x2=−1
。列表
xy′y(−∞,−1)+↗−10−2e4π(−1,0)−↘00−e2π(0,+∞)+↗
由此可见,严格单调增区间为
(−∞,−1)
与
(0,+∞)
;严格单调减区间为
(−1,0)
。
f(0)=−e2π
为极小值,
f(−1)=−2e4π
为极大值。以下求渐近线:
x→∞limf(x)=x→∞lim(x−1)e2π+arctanx=eπx→∞lim(x−1)=∞
所以此函数无水平渐近线;同理,也没有铅直渐近线。令
a1=x→+∞limxf(x)=eπ,b1=x→+∞lim[f(x)−a1x]=−2eπ;
a2=x→−∞limxf(x)=1,b2=x→−∞lim[f(x)−a2x]=−2.
所以,渐近线为
y=a1x+b1=eπ(x−2)
及
y=a2x+b2=x−2
,共两条。
15
设
In=∫04πsinnxcosxdx,n=0,1,2,⋯
,求
∑n=0∞In
.
【答案】
【解析】
首先,计算
In=∫04πsinnxcosxdx
。令
u=sinx
,则
du=cosxdx
,积分限变为
u=0
到
u=22
。于是,
In=∫022undu=[n+1un+1]022=n+11(22)n+1. 接下来,求级数:
n=0∑∞In=n=0∑∞n+11(22)n+1. 令
k=n+1
,则
n=0∑∞In=k=1∑∞k1(22)k=k=1∑∞k1(21)k. 该级数为
∑k=1∞kxk
在
x=21
处的值,其中
∣x∣<1
,且已知
∑k=1∞kxk=−ln(1−x)
。因此,
简化表达式:
所以
−ln(22−1)=−[ln(2−1)−ln2]=ln2−ln(2−1). 由于
ln2=21ln2
和
2−1=2+11
,有
ln(2−1)=ln(2+11)=−ln(2+1), 因此
n=0∑∞In=21ln2+ln(2+1)=ln(2(2+1))=ln(2+2). 故答案为
ln(2+2)
.
16
同试卷 1 第 17 题
17
设向量组
α1=(a,2,10)T
,
α2=(−2,1,5)T
,
α3=(−1,1,4)T,β=(1,b,c)T
.
试问
a,b,c
满足什么条件时,
(1)
β
可由
α1,α2,α3
线性表示,且表示唯一?
(2)
β
不能由
α1,α2,α3
线性表示?
(3)
β
可由
α1,α2,α3
线性表示,但表示不唯一?并求出一般表达式.
【答案】
(1) 当
a=−4
时,
β
可由
α1,α2,α3
唯一线性表示,且
b,c
任意。
(2) 当
a=−4
且
c=3b−1
时,
β
不能由
α1,α2,α3
线性表示。
(3) 当
a=−4
且
c=3b−1
时,
β
可由
α1,α2,α3
线性表示但表示不唯一,且一般表达式为
β=kα1+(−b−1−2k)α2+(2b+1)α3
,其中
k
为任意常数。
【解析】
设方程组
a1x1+a2x2+a3x3=β
。该方程组的系数行列式
∣A∣=∣α1,α2,α3∣=a210−215−114=a20−210−11−1=−a−4. (I) 当
a=−4
时,
∣A∣=0
,方程组有唯一解,
β
可由
α1,α2,α3
线性表示,且表示唯一。
(II) 当
a=−4
时,对增广矩阵作初等行变换,得
(α1,α2,α3,β)=−4210−2151141bc⟶200100010−b−12b+1c−3b+1 因此当
a=−4
且
c−3b+1=0
时,
r(α1,α2,α3)=2=r(α1,α2,α3,β)=3
,方程组无解,
β
不能由
α1,α2,α3
线性表示。
(III) 当
a=−4
且
c−3b+1=0
时,
r(α1,α2,α3)=r(α1,α2,α3,β)=2
,方程组有无穷多解,其通解为
x1x2x3=k1−20+0−(b+1)2b+1=k−2k−b−12b+1, 其中
k
是任意常数。从而
β=kα1+(−2k−b−1)α2+(2b+1)α3,
k
是任意常数。
18
设有
n
元实二次型
f(x1,x2,⋯,xn)=(x1+a1x2)2+(x2+a2x3)2+⋯+(xn−1+an−1xn)2+(xn+anx1)2,
其中
ai=(i=1,2,⋯,n)
为实数.试问:当
a1,a2,⋯,an
满足何种条件时,
二次型
f(x1,x2,⋯,xn)
为正定二次型?
【答案】 当且仅当
a1a2⋯an=(−1)n
时,二次型
f(x1,x2,⋯,xn)
为正定二次型。
【解析】
由题设条件知,对于任意的
x1,x2,⋯,xn
均有
f(x1,x2,⋯,xn)≥0
,其中等号成立当且仅当
⎩⎨⎧x1+a1x2=0,x2+a2x3=0,⋯⋯⋯⋯xn−1+an−1xn=0,xn+anx1=0. 此方程组仅有零解的充分必要条件是其系数行列式
B=100⋮0ana110⋮000a21⋮00⋯⋯⋯⋱⋯⋯000⋮10000⋮an−11=1+(−1)n+1a1a2⋯an=0. 所以当
a1⋅a2⋯an=(−1)n
时,对任意的非零向量
X=(x1,x2,⋯,xn)=0
,方程组中总有一个方程不为零,则有
f(x1,x2,⋯,xn)=(x1+a1x2)2+(x2+a2x3)2+⋯+(xn−1+an−1xn)2+(xn+anx1)2>0
此时二次型
f(x1,x2,⋯,xn)
是正定二次型。
19
假设0.50,1.25,0.80,2.00是来自总体
X
的简单随机样本值.已知
Y=lnX
服从正态分布
N(μ,1)
.
(1) 求
X
的数学期望
EX
(记
EX
为
b
);
(2) 求
μ
的置信度为0.95的置信区间;
(3) 利用上述结果求
b
的置信度为0.95的置信区间.
【答案】
(1)
b=eμ+21
(2)
μ
的置信度为 0.95 的置信区间为
[−0.98,0.98]
(3)
b
的置信度为 0.95 的置信区间为
[e−0.48,e1.48]≈[0.6188,4.3930]
【解析】
(I) 由正态分布密度函数的定义知,
Y
的概率密度为
f(y)=2π1e−2(y−μ)2,−∞<y<+∞, 于是数学期望
b=E(X)=E(eY)=2π1∫−∞+∞ey⋅e−2(y−μ)2dy=2π1∫−∞+∞et+μ⋅e−21t2dt=eμ+21∫−∞+∞2π1⋅e−21(t−1)2dt=eμ+21. (Ⅱ) 当置信度
1−α=0.95
时,
α=0.05
。查表可知标准正态分布的双侧分位数等于
1.96
。故由
Y∼N(μ,41)
,其中
Y
表示总体
Y
的样本均值,
Y=41(ln0.50+ln0.80+ln1.25+ln2.00)=41ln1=0.
所以参数
μ
的置信度为
0.95
的置信区间为
(Y−1.96×41, Y+1.96×41)=(−0.98, 0.98). (Ⅲ) 由指数函数
ex
的严格单调递增性,有
P{−0.98<μ<0.98}=P{−0.48<μ+21<1.48}=P{e−0.48<eμ+21<e1.48}=P{e−0.48<b<e1.48}=0.95.
因此
b
的置信度为
0.95
的置信区间为
(e−0.48, e1.48)
。
20
设
A,B
是二随机事件;随机变量
X={1,−1,若A出现若A不出现Y={1,−1,若B出现若B不出现
试证明随机变量
X
和
Y
不相关的充分必要条件是
A
与
B
相互独立.
【答案】
随机变量
X
和
Y
不相关的充分必要条件是事件
A
与
B
相互独立。
【解析】
E(X)=1⋅P{A}+(−1)⋅P{Aˉ}=2P{A}−1,
同理可得
E(Y)=2P{B}−1
。现在求
E(XY)
,由于
XY
只有两个可能值
1
和
−1
,所以
E(XY)=1⋅P{XY=1}+(−1)⋅P{XY=−1},
其中
P{XY=1}=P{X=1,Y=1}+P{X=−1,Y=−1}=P{AB}+P{AB}=2P{AB}−P{A}−P{B}+1,
P{XY=−1}=P{X=1,Y=−1}+P{X=−1,Y=1}=P{ABˉ}+P{AˉB}=P{A}+P{B}−2P{AB}.
所以
E(XY)=P{XY=1}−P{XY=−1}=4P{AB}−2P{A}−2P{B}+1.
由协方差公式,
Cov(XY)=E(XY)−E(X)E(Y)=4P{AB}−2P{A}−2P{B}+1−[2P{A}−1]⋅[2P{B}−1]=4[P{AB}−P{A}P{B}].
因此,
Cov(XY)=0
当且仅当
P{AB}=P{A}P{B}
,即
X
和
Y
不相关的充分必要条件是
A
与
B
相互独立。