卷 3
填空题
本题共5小题,每小题3分,满分15分
1
设常数
a=21
,则
limn→∞ln[n(1−2a)n−2na+1]n=
______.
【答案】
1−2a1
【解析】
原极限为
limn→∞ln[n(1−2a)n−2na+1]n
。利用对数性质
ln(xn)=nlnx
,可重写为:
n→∞limnln(n(1−2a)n−2na+1)
令
b=1−2a
,由于
a=21
,有
b=0
。则分子为
nb+1
,分母为
nb
,因此:
nln(nbnb+1)=nln(1+nb1)
当
n→∞
时,
nb1→0
,利用等价无穷小
ln(1+x)∼x
(当
x→0
),得:
nln(1+nb1)∼n⋅nb1=b1
故极限为
b1=1−2a1
。也可通过泰勒展开验证:
nln(1+nb1)=n(nb1−2n2b21+O(n31))=b1−2nb21+O(n21)→b1
因此,极限为
1−2a1
。
2
交换积分次序:
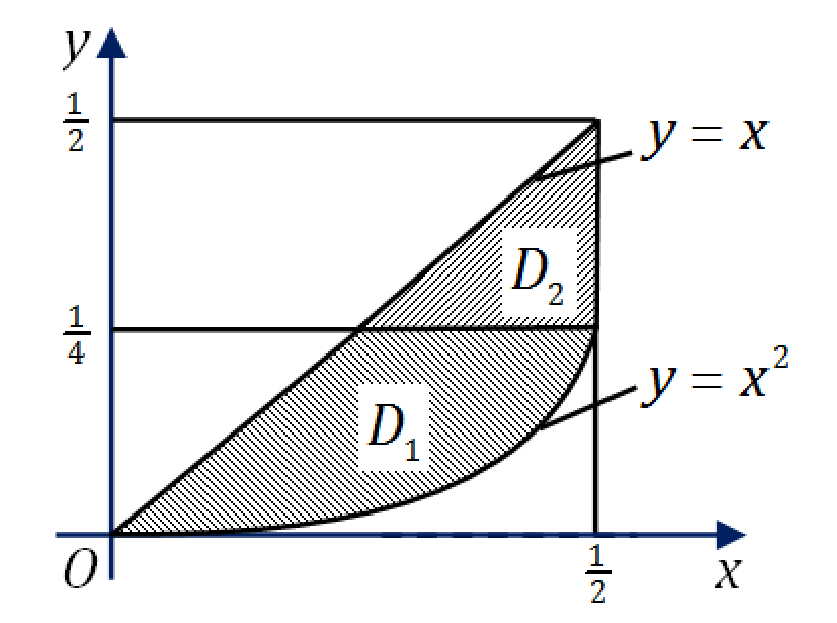
∫041dy∫yyf(x,y)dx+∫4121dy∫y21f(x,y)dx=
______.
【答案】
∫021dx∫x2xf(x,y)dy
【解析】
应填
∫021dx∫x2xf(x,y)dy
。画出与原题中二次积分的积分区域
D1
与
D2
,将它们的并集记为
D
。
于是交换积分次序之后得到
∫041dy∫yyf(x,y)dx+∫4121dy∫y21f(x,y)dx=∬Df(x,y)dσ=∫021dx∫x2xf(x,y)dy. 3
设三阶矩阵
A=123210−224
,三维列向量
α=(a,1,1)T
.
已知
Aα
与
α
线性相关,则
a=
______.
【答案】
-1
【解析】
已知
Aα
与
α
线性相关,故存在标量
λ
使得
Aα=λα
。计算
Aα
:
Aα=123210−224a11=a+2−22a+1+23a+0+4=a2a+33a+4. 代入
Aα=λα
得:
对应分量相等:
- a=λa
,
- 2a+3=λ
,
- 3a+4=λ
.
由方程2和3得
2a+3=3a+4
,解得
a=−1
。代入方程1:当
a=−1
时,
−1=λ(−1)
,得
λ=1
,与方程2和3一致。若
a=0
,则方程2和3矛盾,故唯一解为
a=−1
。
4
设随机变量
X
和
Y
的联合概率分布为
X╲Y01−10.070.0800.180.3210.150.20
则
X2
和
Y2
的协方差
Cov(X2,Y2)=
______.
【答案】
-0.02
【解析】
应填 -0.02。事实上,
X2
、
Y2
和
X2Y2
都是 0-1 分布,而且
P{X2=0}=P{X=0}=0.4,
P{Y2=0}=P{Y=0}=0.5,
P{Y2=1}=P{Y=−1}+P{Y=1}=0.15+0.35=0.5.
同理可求得
X2Y2
的分布律为
X2Y2P00.7210.28
所以得到
E(X2)=0.5,E(Y2)=0.60,E(X2Y2)=0.28.
Cov(X2,Y2)=E(X2Y2)−E(X2)E(Y2)=0.28−0.6×0.5=−0.02.
5
设总体
X
的概率密度为
f(x;θ)={e−(x−θ),0,若x≥θ,若x<θ.
而
X1,X2,⋯,Xn
是来自总体
X
的简单随机样本,则未知参数
θ
的矩估计量为 ______.
【答案】
θ^=Xˉ−1
,其中
Xˉ=n1∑i=1nXi
【解析】
总体
X
的概率密度函数为
f(x;θ)=e−(x−θ)
,当
x≥θ
,否则为 0。计算总体均值
E[X]
:
E[X]=∫θ∞xe−(x−θ)dx
令
t=x−θ
,则
x=t+θ
,
dx=dt
,积分限变为
t=0
到
∞
:
E[X]=∫0∞(t+θ)e−tdt=∫0∞te−tdt+θ∫0∞e−tdt
其中
∫0∞te−tdt=1
,
∫0∞e−tdt=1
,所以
E[X]=1+θ
根据矩估计法,令样本均值
Xˉ=n1∑i=1nXi
等于总体均值
E[X]
:
Xˉ=θ+1
解得矩估计量为
θ^=Xˉ−1
。
选择题
本题共5小题,每小题3分,共15分
6
设函数
f(x)
在闭区间
[a,b]
上有定义,在开区间
(a,b)
内可导,则
正确答案:B【解析】 函数
f(x)
在闭区间
[a,b]
上有定义,在开区间
(a,b)
内可导。由于可导必然连续,因此
f(x)
在开区间
(a,b)
内连续。
对于选项 B,对任何
ξ∈(a,b)
,有
x→ξlim[f(x)−f(ξ)]=0,
这等价于函数在
ξ
处连续,因此 B 正确。
选项 A 要求函数在闭区间上连续才能应用零点定理,但题设未保证函数在端点连续,因此 A 不一定成立。
选项 C 是罗尔定理的形式,但罗尔定理要求函数在闭区间上连续,题设未保证此条件,因此 C 不一定成立。
选项 D 是拉格朗日中值定理的形式,同样要求函数在闭区间上连续,题设未保证此条件,因此 D 不一定成立。
7
设幂级数
∑n=1∞anxn
与
∑n=1∞bnxn
的收敛半径分别为
35
与
31
,则幂级数
∑i=1∞bn2an2xn
的收敛半径为
正确答案:A【解析】
由题设,
所以
n→∞liman+12/bn+12an2/bn2=n→∞limbn2/bn+12an2/an+12=1/35/3=5,
从而所求幂级数的收敛半径为
5
。
8
设
A
是
m×n
矩阵,
B
是
n×m
矩阵,则线性方程组
(AB)x=0
正确答案:D【解析】
设
A
是
m×n
矩阵,
B
是
n×m
矩阵,则
AB
是
m×m
矩阵。
线性方程组
(AB)x=0
有非零解当且仅当系数矩阵
AB
的秩小于
m
,即
rank(AB)<m
。
当
m>n
时,由于
rank(A)≤min(m,n)=n
和
rank(B)≤min(n,m)=n
,因此
rank(AB)≤min(rank(A),rank(B))≤n<m,
故
rank(AB)<m
,方程组必有非零解。
当
n>m
时,
rank(AB)
可能等于
m
也可能小于
m
,因此不一定有非零解或仅有零解,故选项 A 和 B 错误。
选项 C 错误,因为当
m>n
时必有非零解。
因此正确答案为 D。
9
设
A
是
n
阶实对称矩阵,
P
是
n
阶可逆矩阵,已知
n
维列向量
α
是
A
的属于特征值
λ
的特征向量,
则矩阵
(P−1AP)T
属于特征值
λ
的特征向量是
正确答案:B【解析】
已知
A
是实对称矩阵,故
AT=A
。
矩阵
B=P−1AP
与
A
相似,具有相同的特征值
λ
,且
B
属于特征值
λ
的特征向量为
P−1α
。
现在考虑
BT=(P−1AP)T=PTA(P−1)T,
需要求
BT
属于特征值
λ
的特征向量。
设
v
满足
BTv=λv
,即
PTA(P−1)Tv=λv.
令
w=(P−1)Tv
,则
v=PTw
,代入方程得
PTAw=λPTw.
由于
PT
可逆,两边左乘
(PT)−1
得
Aw=λw,
故
w
是
A
的属于特征值
λ
的特征向量。
已知
α
是此类特征向量,因此
w=kα
(
k
为标量),从而
v=PTw=kPTα.
忽略标量倍数,
BT
属于特征值
λ
的特征向量为
PTα
,对应选项 B。其他选项均不满足特征方程。
10
设随机变量
X
和
Y
都服从标准正态分布,则
正确答案:C【解析】
由于
X
和
Y
都服从标准正态分布,即
X∼N(0,1)
和
Y∼N(0,1)
,根据卡方分布的定义,标准正态随机变量的平方服从自由度为 1 的卡方分布,因此
X2∼χ2(1)
和
Y2∼χ2(1)
,无论
X
和
Y
是否独立,选项 C 总是成立。
选项 A 中,
X+Y
不一定服从正态分布,如果
X
和
Y
不独立(例如
Y=−X
时,
X+Y=0
,不是正态分布)。
选项 B 中,
X2+Y2
不一定服从
χ2
分布,如果
X
和
Y
不独立(例如
Y=X
时,
X2+Y2=2X2
,不是
χ2
分布)。
选项 D 中,
X2/Y2
不一定服从
F
分布,如果
X
和
Y
不独立(例如
Y=X
时,
X2/Y2=1
,不是
F
分布)。
因此,只有选项 C 正确。
解答题
11
求极限
x→0limx(1−cosx)∫0x[∫0u2arctan(1+t)dt]du
【答案】
6π
【解析】
由等价无穷小量代换和洛必达法则,可得
x→0limx(1−cosx)∫0x[∫0u2arctan(1+t)dt]du=x→0lim21x3∫0x[∫0u2arctan(1+t)dt]du=x→0lim23x2∫0x2arctan(1+t)dt=x→0lim3xarctan(1+x2)⋅2x=32⋅4π=6π.
12
设函数
u=f(x,y,z)
有连续偏导数,且
z=z(x,y)
由方程
xex−yey=zez
所确定,求
du
.
【答案】
du=(∂x∂f+∂z∂f⋅ez(1+z)ex(1+x))dx+(∂y∂f−∂z∂f⋅ez(1+z)ey(1+y))dy
【解析】
函数
u=f(x,y,z)
有连续偏导数,且
z=z(x,y)
由方程
xex−yey=zez
所确定。求
du
即求全微分。
首先,由全微分公式,有:
du=∂x∂fdx+∂y∂fdy+∂z∂fdz
其中
dz
需要通过隐函数求导得到。设
F(x,y,z)=xex−yey−zez=0
,则:
∂x∂F=ex(1+x),∂y∂F=−ey(1+y),∂z∂F=−ez(1+z)
由隐函数定理:
∂x∂z=−∂z∂F∂x∂F=ez(1+z)ex(1+x),∂y∂z=−∂z∂F∂y∂F=−ez(1+z)ey(1+y)
代入
dz=∂x∂zdx+∂y∂zdy
到
du
表达式中,合并同类项即得结果。
13
设
f(sin2x)=sinxx
,求
∫1−xxf(x)dx
.
【答案】
∫1−xxf(x)dx=−21−xarcsin(x)+2x+C 其中
C
为积分常数。
【解析】
给定
f(sin2x)=sinxx
,令
u=sin2x
,则
sinx=u
(取主值),
x=arcsin(u)
,所以
f(u)=uarcsin(u)
,即
f(x)=xarcsin(x)
。
代入积分:
∫1−xxf(x)dx=∫1−xx⋅xarcsin(x)dx=∫1−xarcsin(x)dx. 令
t=x
,则
x=t2
,
dx=2tdt
,代入得:
∫1−t2arcsin(t)⋅2tdt=2∫1−t2tarcsin(t)dt. 使用分部积分法,令
u=arcsin(t)
,
du=1−t21dt
,
dv=1−t2tdt
,则
v=∫1−t2tdt=−1−t2
。
于是:
∫1−t2tarcsin(t)dt=arcsin(t)⋅(−1−t2)∫(−1−t2)⋅1−t21dt=−arcsin(t)1−t2+∫1dt=−arcsin(t)1−t2+t+C. 所以:
2∫1−t2tarcsin(t)dt=2(−arcsin(t)1−t2+t+C)=−2arcsin(t)1−t2+2t+C. 代回
t=x
,得:
∫1−xxf(x)dx=−21−xarcsin(x)+2x+C. 14
设
D1
是由抛物线
y=2x2
和直线
x=a
,
x=2
及
y=0
所围成的平面区域;
D2
是由抛物线
y=2x2
和直线
y=0
,
x=a
所围成的平面区域,其中
0<a<2
.
(1) 试求
D1
绕
x
轴旋转而成的旋转体体积
V1
;
D2
绕
y
轴旋转而成的旋转体体积
V2
;
(2) 问当
a
为何值时,
V1+V2
取得最大值?试求此最大值.
【答案】
(1)
V1=54π(32−a5)
,
V2=πa4
(2) 当
a=1
时,
V1+V2
取得最大值,最大值为
5129π
【解析】
(I) 由旋转体的体积公式有
V1=π∫a2(2x2)2dx=54π(32−a5),
V2=πa2⋅2a2−π∫02a2x2dy=πa4.
(II)
V=V1+V2=54π(32−a5)+πa4
. 令
dadV=4πa3(1−a)=0
,得
a=1
. 当
0<a<1
时
dadV>0
,当
1<a<2
时
dadV<0
,因此
a=1
是
V
的唯一极值点且是极大值点,所以是
V
的最大值点,
Vmax=5129π
15
同试卷 1 第 15 题
16
设函数
f(x),g(x)
在
[a,b]
上连续,且
g(x)>0
.利用闭区间上连续函数性质,
证明存在一点
ξ∈[a,b]
,使
∫abf(x)g(x)dx=f(ξ)∫abg(x)dx
.
【答案】 见解析
【解析】
因为
f(x)
与
g(x)
在
[a,b]
上连续,所以存在
x1,x2
使得
f(x1)=M=x∈[a,b]maxf(x),f(x2)=m=x∈[a,b]minf(x).
满足
m≤f(x)≤M
。又
g(x)>0
,故根据不等式的性质
mg(x)≤f(x)g(x)≤Mg(x).
根据定积分的不等式性质有
m∫abg(x)dx≤∫abf(x)g(x)dx≤M∫abg(x)dx
⇒m≤∫abg(x)dx∫abf(x)g(x)dx≤M.
由连续函数的介值定理知,存在
ξ∈[a,b]
,使
f(ξ)=∫abg(x)dx∫abf(x)g(x)dx⇒∫abf(x)g(x)dx=f(ξ)∫abg(x)dx.
17
设齐次线性方程组
⎩⎨⎧ax1+bx2+bx3+⋯+bxn=0,bx1+ax2+bx3+⋯+bxn=0,⋯⋯⋯⋯bx1+bx2+bx3+⋯+axn=0,
其中
a=0,b=0,n≥2
,
试讨论
a,b
为何值时,方程组仅有零解、有无穷多组解?
在有无穷多组解时,求出全部解,并用基础解系表示全部解.
【答案】
当
a=b
且
a=−b(n−1)
时,方程组仅有零解。
当
a=b
或
a=−b(n−1)
时,方程组有无穷多组解。
- 当
a=b
时,全部解为
x=k1ξ1+k2ξ2+⋯+kn−1ξn−1
,其中
ξ1=(1,−1,0,…,0)T
,
ξ2=(1,0,−1,…,0)T
,
…
,
ξn−1=(1,0,0,…,−1)T
,
k1,k2,…,kn−1
为任意常数。
- 当
a=−b(n−1)
时,全部解为
x=kξ
,其中
ξ=(1,1,1,…,1)T
,
k
为任意常数。
【解析】
方程组的系数行列式
∣A∣=abb⋮bbab⋮bbba⋮b⋯⋯⋯⋱⋯bbb⋮a=[a+(n−1)b](a−b)n−1. (I) 当
a=b
且
a=−(n−1)b
时,
∣A∣=0
,
r(A)=n
,方程组只有零解。
(II) 当
a=b(=0)
时,对系数矩阵
A
做行初等变换,有
A=aaa⋮aaaa⋮aaaa⋮a⋯⋯⋯⋱⋯aaa⋮a→a00⋮0a00⋮0a00⋮0⋯⋯⋯⋱⋯a00⋮0→100⋮0100⋮0100⋮0⋯⋯⋯⋱⋯100⋮0. 方程组的同解方程组为
x1+x2+⋯+xn=0
,其基础解系为
ξ1=(−1,1,0,⋯,0)T,ξ2=(−1,0,1,0,⋯,0)T,
⋯,ξn−1=(−1,0,⋯,0,1)T.
方程组的全部解为
X=k1ξ1+k2ξ2+⋯+kn−1ξn−1,
其中
ki(i=1,2,⋯,n−1)
是任意常数。
(Ⅲ) 当
a=−(n−1)b
(
b=0
) 时,对系数矩阵
A
做行初等变换,有
A=(1−n)bbb⋮bb(1−n)bb⋮bbb(1−n)b⋮b⋯⋯⋯⋱⋯bbb⋮(1−n)b →1−n11⋮111−n1⋮1111−n⋮1⋯⋯⋯⋱⋯111⋮1−n→1−nnn⋮n1−n0⋮010−n⋮0⋯⋯⋯⋱⋯100⋮−n →1−n11⋮11−10⋮010−1⋮0⋯⋯⋯⋱⋯100⋮−1→011⋮10−10⋮000−1⋮0⋯⋯⋯⋱⋯000⋮−1. 秩
r(A)=n−1
,其同解方程组是
⎩⎨⎧x1−x2=0,x1−x3=0,⋯⋯x1−xn=0. 其基础解系为
ξ=(1,1,⋯,1)T
,方程组的全部解为
X=kξ
,其中
k
是任意常数。
18
设
A
为三阶实对称矩阵,且满足条件
A2+2A=0
,已知
A
的秩
r(A)=2
.
(1) 求
A
的全部特征值.
(2) 当
k
为何值时,矩阵
A+kE
为正定矩阵,其中
E
为三阶单位矩阵.
【答案】
(1)
0,−2,−2
(2)
k>2
【解析】
(I) 设
λ
是
A
的特征值,
α
是
A
的属于
λ
的特征向量,则有
Aα=λα
,从而
0=(A2+2A)α=(λ2+2λ)α.
所以有
λ2+2λ=0
,故
A
的特征值
λ
的取值范围为
0,−2
。因为实对称矩阵必可对角化,
r(A)=2
,所以
即
A
有特征值
λ1=λ2=−2
,
λ3=0
。
(II) 由 (I) 知
A+kE
的特征值为
k−2,k−2,k
。矩阵
A+kE
正定的充要条件是它的所有特征值均大于零,即
{k−2>0k>0⟺k>2.
故
k>2
时
A+kE
是正定矩阵。
19
假设随机变量
U
在区间
[−2,2]
上服从均匀分布,随机变量
X={−1,1,若U≤−1,若U>−1;Y={−1,1,若U≤1,若U>1;
试求:
(1)
X
和
Y
的联合概率分布;
(2)
D(X+Y)
.
【答案】
(1)
X
和
Y
的联合概率分布为:
X=−1X=1Y=−14121Y=1041
(2)
D(X+Y)=2
【解析】
(I)
(X,Y)
只有四个可能值
(−1,−1)
,
(−1,1)
,
(1,−1)
和
(1,1)
. 依题意有
P{X=−1,Y=−1}=P{U⩽−1,U⩽1}=P{U⩽−1}=41;
P{X=−1,Y=1}=P{U⩽−1,U>1}=P{∅}=0;
P{X=1,Y=−1}=P{U>−1,U⩽1}=P{−1<U⩽1}=21;
P{X=1,Y=1}=P{U>−1,U>1}=P{U>1}=41.
于是,
(X,Y)
分布为
YX−11−141211041
(II)
X+Y
的取值可能有
−2,0,2
;
(X+Y)2
的取值可能有 0 和 4;
P{X+Y=−2}=P{X=−1,Y=−1}=41,
P{X+Y=0}=P{X=1,Y=−1}+P{X=−1,Y=1}=0+21=21,
P{X+Y=2}=P{X=1,Y=1}=41,
P{(X+Y)2=0}=P{X+Y=0}=21,
P{(X+Y)2=4}=P{X+Y=−2}+P{X+Y=2}=21
故
X+Y
和
(X+Y)2
的分布律分别为
(X+Y)2P021421X+YP−241021241
由此可见
E(X+Y)=−42+42=0,E(X+Y)2=24=2,
D(X+Y)=E(X+Y)2−[E(X+Y)]2=2.
20
假设一设备开机后无故障工作的时间
X
服从指数分布,平均无故障工作的时间
E(X)
为
5
小时.
设备定时开机,出现故障时自动关机,而在无故障的情况下工作
2
小时便关机.
试求该设备每次开机无故障工作的时间
Y
的分布函数
F(y)
.
【答案】
F(y)=⎩⎨⎧01−e−0.2y1 y<0 0≤y<2 y≥2 【解析】
指数分布的
X
的分布参数为
λ=E(X)1=51
,其密度函数为
fX(x)={51e−51x,0,x>0;x≤0.
由分布函数的定义,
F(y)=P{Y≤y}=P{min(X,2)≤y}.
当
y<0
时,
FY(y)=0
。当
y≥2
时,
FY(y)=1
。当
0≤y<2
时,
F(y)=P{min(X,2)≤y}=P{X≤y}=∫−∞yfX(x)dx=∫0y51e−51xdx=1−e−51y.
所以
Y
的分布函数
FY(y)=⎩⎨⎧0,1−e−51y,1,y<0;0≤y<2;y≥2.