卷 2
填空题
本题共6小题,每小题4分,满分24分
1
若
x→0
时,
(1−ax2)41−1
与
xsinx
是等价无穷小,则
a=
______.
【答案】
−4
【解析】
当
x→0
时,等价无穷小要求
limx→0xsinx(1−ax2)41−1=1
。
由于
xsinx∼x2
,极限化为
limx→0x2(1−ax2)41−1=1
。
利用等价无穷小替换,当
u→0
时,
(1+u)n−1∼nu
,这里
u=−ax2
,
n=41
,
所以
(1−ax2)41−1∼41(−ax2)=−4ax2
。
代入极限得
limx→0x2−4ax2=−4a=1
,
解得
a=−4
。
2
设函数
y=f(x)
由方程
xy+2lnx=y4
所确定,则曲线
y=f(x)
在点(1,1)处的切线方程是 ______.
【答案】
y=x
【解析】
给定方程
xy+2lnx=y4
,点
(1,1)
满足该方程。
对方程两边关于
x
求导,注意
y
是
x
的函数:
左边导数为
y+xdxdy+x2
,右边导数为
4y3dxdy
。
于是有:
y+xdxdy+x2=4y3dxdy
代入点
(1,1)
:
1+1⋅dxdy+12=4⋅13⋅dxdy
简化得:
1+dxdy+2=4dxdy3+dxdy=4dxdy3=3dxdydxdy=1
因此,在点
(1,1)
处的切线斜率为 1。
切线方程为:
y−1=1⋅(x−1)
即
y=x
。
3
y=2x
的麦克劳林公式中
xn
项的系数是 ______.
【答案】
n!(ln2)n
【解析】
函数
y=2x
的麦克劳林公式是其在
x=0
处的泰勒级数展开。首先,将
2x
写为
exln2
,然后求其 n 阶导数。n 阶导数为
f(n)(x)=(ln2)n⋅2x
。在
x=0
处,有
f(n)(0)=(ln2)n
。代入泰勒级数公式
f(x)=∑n=0∞n!f(n)(0)xn
,得到
2x=∑n=0∞n!(ln2)nxn
。因此,
xn
项的系数为
n!(ln2)n
。
4
设曲线的极坐标方程为
ρ=eaθ
(
a>0
),
则该曲线上相应于
θ
从
0
变到
2π
的一段弧与极轴所围成的图形的面积为 ______.
【答案】
4a1(e4aπ−1)
【解析】
在极坐标系中,曲线
ρ=eaθ
(
a>0
) 相应于
θ
从
0
到
2π
的一段弧与极轴所围成的图形的面积公式为:
A=21∫02πρ2dθ
代入
ρ=eaθ
,得:
A=21∫02π(eaθ)2dθ=21∫02πe2aθdθ
计算积分:
∫e2aθdθ=2a1e2aθ
所以:
A=21[2a1e2aθ]02π=21⋅2a1(e4aπ−e0)=4a1(e4aπ−1)
因此,所求面积为
4a1(e4aπ−1)
。
5
设
α
为
3
维列向量,
αT
是
α
的转置.若
ααT=1−11−11−11−11
,则
αTα=
______.
【答案】
3
【解析】
已知
ααT=1−11−11−11−11
。由于
ααT
是秩为1的矩阵,其非零特征值等于
αTα
,而迹等于特征值之和。计算矩阵的迹为
1+1+1=3
,因此
αTα=3
。
Alternatively,设
α=[a,b,c]T
,则
ααT=a2abacabb2bcacbcc2
。与给定矩阵比较,得
a2=1
,
b2=1
,
c2=1
,
ab=−1
,
ac=1
,
bc=−1
。解得
α=[1,−1,1]T
或
α=[−1,1,−1]T
。计算
αTα
,均为
1+1+1=3
。故答案为3。
6
设三阶方阵
A,B
满足
A2B−A−B=E
,其中
E
为三阶单位矩阵,若
A=10−2020101
,则
∣B∣=
______.
【答案】
21
【解析】
已知三阶方阵
A
和
B
满足方程:
A2B−A−B=E,
其中
E
为单位矩阵,且
将方程改写为:
A2B−B=A+E,
即:
(A2−I)B=A+I,
其中
I
为单位矩阵。注意到
A2−I=(A−I)(A+I)
,若
A+I
可逆,则上式可写为:
B=(A2−I)−1(A+I)=[(A−I)(A+I)]−1(A+I)=(A+I)−1(A−I)−1(A+I).
由于矩阵乘积的行列式等于行列式的乘积,且行列式乘法可交换,有:
∣B∣=∣(A+I)−1(A−I)−1(A+I)∣=∣(A+I)−1∣⋅∣(A−I)−1∣⋅∣A+I∣=∣A+I∣1⋅∣A−I∣1⋅∣A+I∣=∣A−I∣1.
因此,只需计算
∣A−I∣
。由
A−I=1−10−202−10101−1=00−2010100, 计算其行列式:
∣A−I∣=00−2010100=1⋅0−210=1⋅(0⋅0−1⋅(−2))=2. 故
∣B∣=∣A−I∣1=21.
因此,
∣B∣=21
。
选择题
本题共6小题,每小题4分,满分24分
7
同试卷 1 第 8 题
8
设
an=23∫0n+1nxn−11+xndx
,
则极限
limn→∞nan
等于
正确答案:B【解析】
给定
an=23∫0n+1nxn−11+xndx
,需要求
limn→∞nan
。
考虑积分
In=∫0n+1nxn−11+xndx
。
令
x=1−ny
,则
dx=−ndy
。
积分限变化:当
x=0
时,
y=n
;当
x=n+1n
时,
y=n+1n≈1
。
于是,
In=∫y=ny=n+1n(1−ny)n−11+(1−ny)n(−ndy)=n1∫y=n+1ny=n(1−ny)n−11+(1−ny)ndy. 当
n→∞
时,
(1−ny)n−1≈e−y
,
(1−ny)n≈e−y
,且被积函数在
y
较大时衰减,主要贡献来自
y
接近 1。
因此,
于是,
令
u=e−y
,则
du=−e−ydy
,即
e−ydy=−du
。
积分限变化:当
y=1
时,
u=e−1
;当
y=∞
时,
u=0
。
所以,
∫1∞e−y1+e−ydy=∫e−101+u(−du)=∫0e−11+udu=[32(1+u)3/2]0e−1=32((1+e−1)3/2−1). 因此,
nIn≈32((1+e−1)3/2−1).
由于
an=23In
,有
nan=n⋅23In=23nIn≈23⋅32((1+e−1)3/2−1)=(1+e−1)3/2−1.
故
limn→∞nan=(1+e−1)23−1
,对应选项 B。
9
已知
y=lnxx
是微分方程
y′=xy+ϕ(yx)
的解,
则
ϕ(yx)
的表达式为
正确答案:A【解析】
已知
y=lnxx
是微分方程
y′=xy+ϕ(yx)
的解。
首先求导
y′
:
由
y=lnxx
,使用商法则,
y′=(lnx)2lnx⋅1−x⋅x1=(lnx)2lnx−1.
代入微分方程:
左边为
y′=(lnx)2lnx−1,
右边为
xy+ϕ(yx).
计算
xy=xlnxx=lnx1,
且
yx=lnxxx=lnx.
于是方程化为
(lnx)2lnx−1=lnx1+ϕ(lnx).
令
t=lnx
,则
t2t−1=t1+ϕ(t).
解得
ϕ(t)=t2t−1−t1=t2t−1−t=−t21.
由于
t=yx
,所以
ϕ(yx)=−(yx)21=−x2y2.
因此,
ϕ(yx)
的表达式为
−x2y2
,对应选项 A。
10
同试卷 1 第 7 题
11
设
I1=∫04πxtanxdx
,
I2=∫04πtanxxdx
,
则
正确答案:B
【解析】 考虑函数
f(x)=xtanx
,则
I1=∫04πf(x)dx
和
I2=∫04πf(x)1dx
。在区间
(0,4π]
上,由于
tanx>x
,有
f(x)>1
,因此
f(x)1<1
。于是
I1>I2
。
通过级数展开估算:
I1≈0.849<1
,
I2≈0.730<1
,故
1>I1>I2
。
选项 B 符合这一结果。
12
同试卷 1 第 10 题
解答题
13
设函数
f(x)=⎩⎨⎧x−arcsinxln(1+ax3),6,xsin4xeax+x2−ax−1,x<0;x=0;x>0. 问
a
为何值时,
f(x)
在
x=0
处连续;
a
为何值时,
x=0
是
f(x)
的可去间断点?
【答案】
连续时
a=−1
,可去间断点时
a=−2
【解析】
因为
f(0)=6
,而单侧极限为
f(0−)=x→0−limf(x)=x→0−limx−arcsinxln(1+ax3)=x→0−limx−arcsinxax3=x→0−lim1−1−x213ax2=x→0−lim1−x2−13ax2⋅x→0−lim1−x2=x→0−lim21x23ax2=−6a, f(0+)=x→0+limf(x)=x→0+limxsin4xeax+x2−ax−1=x→0+lim4x2eax+x2−ax−1=4x→0+limx2eax+x2−ax−1=4x→0+lim2xaeax+2x−a=4x→0+lim2a2eax+2=2x→0+lim(a2eax+2)=2a2+4.
所以,
x=0
为
f(x)
的连续点当且仅当
−6a=6=2a2+4
,即
a=−1
;
x=0
为
f(x)
的可去间断点当且仅当
−6a=2a2+4=6
,即
2a2+6a+4=0
但
a=−1
,即
a=−2
。
14
设函数
y=y(x)
由参数方程
{x=1+2t2,y=∫11+2lntueudu
(
t>1
)所确定,求
dx2d2yx=9
.
【答案】
−16(1+2ln2)2e
【解析】
给定参数方程:
x=1+2t2,y=∫11+2lntueudu(t>1)
求二阶导数
dx2d2yx=9
.
首先,计算一阶导数
dxdy
。
由参数方程求导公式:
dxdy=dtdxdtdy
其中:
dtdx=dtd(1+2t2)=4t
dtdy=dtd(∫11+2lntueudu)=1+2lnte1+2lnt⋅dtd(1+2lnt)=1+2lnte⋅t2⋅t2=1+2lnt2et
因此:
dxdy=4t1+2lnt2et=2(1+2lnt)e
接下来,计算二阶导数
dx2d2y
:
dx2d2y=dxd(dxdy)=dtdxdtd(dxdy)
其中:
dtd(dxdy)=dtd(2(1+2lnt)e)=2e⋅dtd((1+2lnt)−1)=2e⋅(−(1+2lnt)21⋅t2)=−t(1+2lnt)2e
代入:
dx2d2y=4t−t(1+2lnt)2e=−4t2(1+2lnt)2e
当
x=9
时,由
x=1+2t2=9
得
2t2=8
,即
t2=4
,取
t=2
(因
t>1
)。
代入
t=2
:
dx2d2yx=9=−4⋅22⋅(1+2ln2)2e=−16(1+2ln2)2e 故结果为:
−16(1+2ln2)2e
15
计算不定积分
∫(1+x2)3/2xearctanxdx
.
【答案】
【解析】
考虑积分
∫(1+x2)3/2xearctanxdx
。令
t=arctanx
,则
x=tant
,
dx=sec2tdt
,且
earctanx=et
。分母
(1+x2)3/2=(1+tan2t)3/2=(sec2t)3/2=sec3t
。代入得:
∫(1+x2)3/2xearctanxdx=∫sec3ttant⋅et⋅sec2tdt=∫secttant⋅etdt.
由于
tant/sect=sint
,积分化为:
∫sint⋅etdt.
计算
∫sint⋅etdt
,使用分部积分法。令
I=∫etsintdt
,设
u=sint
,
dv=etdt
,则
du=costdt
,
v=et
,得:
I=etsint−∫etcostdt.
对
∫etcostdt
再次分部积分,设
u=cost
,
dv=etdt
,则
du=−sintdt
,
v=et
,得:
∫etcostdt=etcost−∫et(−sint)dt=etcost+∫etsintdt=etcost+I.
代入回
I
:
I=etsint−(etcost+I)=etsint−etcost−I,
整理得:
2I=et(sint−cost),
所以:
I=2et(sint−cost)+C.
代回
t=arctanx
,并利用
sint=1+x2x
,
cost=1+x21
,得:
∫(1+x2)3/2xearctanxdx=2earctanx(1+x2x−1+x21)+C=21+x2(x−1)earctanx+C. 16
同试卷 1 第 17 题
17
讨论曲线
y=4lnx+k
与
y=4x+ln4x
的交点个数.
【答案】
当
k<4
时,交点个数为 0;
当
k=4
时,交点个数为 1;
当
k>4
时,交点个数为 2。
【解析】
考虑曲线
y=4lnx+k
与
y=4x+ln4x
的交点,即方程
4lnx+k=4x+ln4x
。
令
k=4x+ln4x−4lnx
。
设
t=lnx
(其中
x>0
,故
t∈R
),则函数化为
g(t)=4et+t4−4t
。
问题转化为讨论方程
k=g(t)
的解的个数。
求导
g′(t)=4(et+t3−1)
。
令
h(t)=et+t3−1
,则
h′(t)=et+3t2>0
,故
h(t)
严格递增。
当
t=0
时,
h(0)=0
,即
g′(0)=0
,且
t=0
是唯一临界点。
计算
g(0)=4
。
当
t<0
时,
g′(t)<0
,函数单调递减;当
t>0
时,
g′(t)>0
,函数单调递增。
因此,
g(t)
在
t=0
处取得最小值
4
。
当
t→−∞
时,
g(t)→+∞
;当
t→+∞
时,
g(t)→+∞
。
故
g(t)
的值域为
[4,+∞)
。
于是:
- 当
k<4
时,方程
k=g(t)
无解,交点个数为 0;
- 当
k=4
时,方程有唯一解
t=0
(即
x=1
),交点个数为 1;
- 当
k>4
时,方程有两个解(一个
t<0
,一个
t>0
),交点个数为 2。
18
设位于第一象限的曲线
y=f(x)
过点
(22,21)
,
其上任一点
P(x,y)
处的法线与
y
轴的交点为
Q
,且线段
PQ
被
x
轴平分.
(1) 求曲线
y=f(x)
的方程;
(2) 已知曲线
y=sinx
在
[0,π]
上的弧长为
l
,试用
l
表示曲线
y=f(x)
的弧长
s
.
【答案】
(1) 曲线方程为
x2+2y2=1
(其中
x>0,y>0
)。
(2) 曲线
y=f(x)
的弧长
s=22l
。
【解析】
(1) 曲线
y=f(x)
在点
P(x,y)
处的法线方程为
Y−y=−y′1(X−x).
令
X=0
,则它与
y
轴的交点为
Q(0,y+y′x)
。由题设,线段
PQ
被
x
轴平分,从而
21(y+y+y′x)=0⇒2ydy+xdx=0.
积分得
2x2+y2=C(C 为任意常数),
代入初始条件
得
C=21,
故曲线
y=f(x)
的方程为
2x2+y2=21,
即
x2+2y2=1.
(II) 曲线
y=sinx
在
[0,π]
上的弧长为
l=∫0π1+y′2dx=∫0π1+cos2xdx =∫0π1+cos2tdt=2∫02π1+cos2tdt. 另一方面,曲线
y=f(x)
的参数方程为
{x=cost,y=22sint,(0≤t≤2π). 于是该曲线的弧长为(其中换元
u=2π−t
)
s=∫02π(xt′)2+(yt′)2dt=∫02πsin2t+21cos2tdt=21∫02π1+sin2tdt=21∫2π01+cos2u(−du)=21∫02π1+cos2udu. 所以
s=42l
。
19
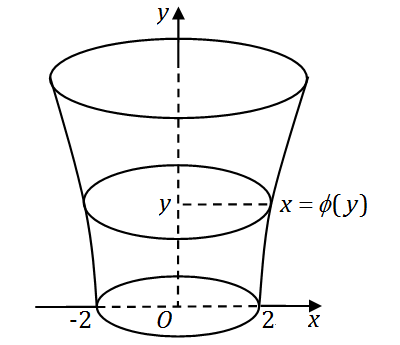
有一平底容器,其内侧壁是由曲线
x=ϕ(y)
(
y≥0
)绕
y
轴旋转而成的旋转曲面(如图),
容器的底面圆的半径为2
m
.根据设计要求,当以
3m3/min
的速率向容器内注入液体时,
液面的面积将以
πm2/min
的速率均匀扩大(假设注入液体前,容器内无液体).
(1) 根据
t
时刻液面的面积,写出
t
与
ϕ(y)
之间的关系式;
(2) 求曲线
x=ϕ(y)
的方程.
(注:
m
表示长度单位米,
min
表示时间单位分.)
【答案】
(1)
t=[ϕ(y)]2−4
(2)
x=2e6πy
【解析】
(1) 设
t
时刻液面的高度为
y
,液面的半径为
ϕ(y)
,液面的面积为
A=π[ϕ(y)]2.
根据设计要求,液面面积以
πm2/min
的速率均匀扩大,即
dtdA=π.
积分得
A=πt+C.
当
t=0
时,容器内无液体,液面在底面,底面半径为
2m
,所以
A=π×22=4π.
代入得
C=4π
,因此
A=πt+4π.
由
A=π[ϕ(y)]2
得
π[ϕ(y)]2=πt+4π,
即
[ϕ(y)]2=t+4,
所以
t=[ϕ(y)]2−4.
(2) 容器内液体的体积
V=π∫0y[ϕ(u)]2du.
注入液体的速率
dtdV=3.
由
dtdV=π[ϕ(y)]2dtdy=3
得
[ϕ(y)]2dtdy=π3.
又由液面面积变化率
dtdA=2πϕ(y)ϕ′(y)dtdy=π
得
2ϕ(y)ϕ′(y)dtdy=1.
将前式代入后式得
2ϕ(y)ϕ′(y)⋅π[ϕ(y)]23=1,
即
πϕ(y)6ϕ′(y)=1,
所以
ϕ(y)ϕ′(y)=6π.
积分得
lnϕ(y)=6πy+C,
即
ϕ(y)=C1e6πy.
由初始条件
ϕ(0)=2
得
C1=2
,所以曲线方程为
x=ϕ(y)=2e6πy.
20
设函数
f(x)
在闭区间
[a,b]
上连续,在开区间
(a,b)
内可导,且
f′(x)>0
.
若极限
limx→a+x−af(2x−a)
存在,证明:
(1) 在
(a,b)
内
f(x)>0
;
(2) 在
(a,b)
内存在点
ξ
,使
∫abf(x)dxb2−a2=f(ξ)2ξ
;
(3) 在
(a,b)
内存在与(2)中
ξ
相异的点
η
,使
f′(η)(b2−a2)=ξ−a2ξ∫abf(x)dx
.
【解析】
(Ⅰ) 因为
limx→a+x−af(2x−a)
存在,且
limx→a+(x−a)=0
,故
limx→a+f(2x−a)=0
。又
f(x)
在
[a,b]
上连续,从而
limx→a+f(2x−a)=f(a)
,则
f(a)=0
。由于
f′(x)>0
,则
f(x)
在
(a,b)
内严格单调增加,所以
f(x)
在
x=a
处取最小值,即
f(x)>f(a)=0
,
x∈(a,b)
。
(Ⅱ) 取
F(x)=x2
,
g(x)=∫axf(t)dt
(
a≤x≤b
),则
g′(x)=f(x)>0
,则
F(x)
、
g(x)
满足柯西中值定理的条件,于是在
(a,b)
内存在点
ξ
,使
g(b)−g(a)F(b)−F(a)=∫abf(t)dt−∫aaf(t)dtb2−a2=f(ξ)2ξ⇒∫abf(x)dxb2−a2=f(ξ)2ξ.
(Ⅲ) 在区间
[a,ξ]
上应用拉格朗日中值定理,得在
(a,ξ)
内存在一点
η
,使
f(ξ)−f(a)=f′(η)(ξ−a).
因
f(a)=0
,上式即
f(ξ)=f′(η)(ξ−a)
,代入 (Ⅱ) 的结论得
∫abf(x)dxb2−a2=f′(η)(ξ−a)2ξ⇒f′(η)(b2−a2)=ξ−a2ξ∫abf(x)dx.
21
若矩阵
A=2802200a6
相似于对角阵
Λ
,试确定常数
a
的值;并求可逆矩阵
P
使
P−1AP=Λ
.
【答案】
a=0
,可逆矩阵
P=1200011−20
,对角阵
Λ=60006000−2
。
【解析】
矩阵
A
相似于对角阵的条件是代数重数等于几何重数。计算特征多项式:
det(A−λI)=det2−λ8022−λ00a6−λ=(6−λ)[(2−λ)2−16]=(6−λ)(λ2−4λ−12)=(6−λ)(λ−6)(λ+2)=−(λ−6)2(λ+2). 特征值为
λ=6
(代数重数2)和
λ=−2
(代数重数1)。
对于
λ=6
,计算几何重数:
要求几何重数为2,则矩阵秩为1。当
a=0
时,第二行是第一行的倍数,秩为1,故
a=0
。
当
a=0
时,求特征向量:
对于
λ=6
,解
(A−6I)x=0
:
−4802−40000x1x2x3=0, 得
x2=2x1
,
x3
自由,特征向量为
120
和
001
。
对于
λ=−2
,解
(A+2I)x=0
:
得
x2=−2x1
,
x3=0
,特征向量为
1−20
。
取可逆矩阵
P
由特征向量组成:
对角阵
Λ=60006000−2
,满足
P−1AP=Λ
。
22
同试卷 1 第 20 题