卷 3
填空题
1~6小题,每小题4分,共24分
1
若
limx→0ex−asinx(cosx−b)=5
,则
a=
______,
b=
______.
【答案】
a=1
,
b=−4
【解析】
给定极限
limx→0ex−asinx(cosx−b)=5
。
当
x→0
时,
sinx→0
,
ex→1
,
cosx→1
。
若
a=1
,则
ex−a→1−a=0
,且
sinx(cosx−b)→0
,因此极限为
0
,与极限值为
5
矛盾。
故
a=1
,此时极限化为
x→0limex−1sinx(cosx−b)
利用等价无穷小,当
x→0
时,
sinx∼x
,
ex−1∼x
,因此
ex−1sinx∼1
于是极限近似为
x→0lim(cosx−b)=cos0−b=1−b
设
1−b=5
,得
b=−4
。
验证:当
a=1
,
b=−4
时,
x→0limex−1sinx(cosx+4)→1×(1+4)=5
符合条件。
因此,
a=1
,
b=−4
。
2
函数
f(u,v)
由关系式
f[xg(y),y]=x+g(y)
确定,其中函数
g(y)
可微,
且
g(y)=0
,则
∂u∂v∂2f=
______.
【答案】
−g2(y)g′(y)
【解析】
给定函数关系式
f[xg(y),y]=x+g(y)
,其中
g(y)
可微且
g(y)=0
。
令
u=xg(y)
,
v=y
,则
x=g(v)u
。代入关系式得:
f(u,v)=g(v)u+g(v)
对
f(u,v)
求偏导数:
首先,对
u
求偏导:
∂u∂f=g(v)1
然后,对
v
求偏导:
∂u∂v∂2f=∂v∂(g(v)1)=−g2(v)1⋅g′(v)=−g2(v)g′(v)
由于
v=y
,故
∂u∂v∂2f=−g2(y)g′(y)
3
设
f(x)={xex2,−1,−21≤x<21,x≥21,
,则
∫212f(x−1)dx=
..
【答案】
−21
【解析】
需要计算积分
∫212f(x−1)dx
。令
u=x−1
,则当
x=21
时,
u=−21
;当
x=2
时,
u=1
。积分变为:
∫212f(x−1)dx=∫−211f(u)du
函数
f(u)
定义为:
f(u)={ueu2,−1,−21≤u<21,u≥21.
将积分拆分为两部分:
∫−211f(u)du=∫−2121f(u)du+∫211f(u)du
在第一部分区间
[−21,21)
上,
f(u)=ueu2
。函数
ueu2
是奇函数,且在对称区间上积分,故:
∫−2121ueu2du=0
在第二部分区间
[21,1]
上,
f(u)=−1
,故:
∫211(−1)du=−[u]211=−(1−21)=−21
因此,积分结果为:
0+(−21)=−21
4
二次型
f(x1,x2,x3)=(x1+x2)2+(x2−x3)2+(x3+x1)2
的秩为 ______.
【答案】
2
【解析】
因为
f(x1,x2,x3)=(x1+x2)2+(x2−x3)2+(x3+x1)2
=2x12+2x22+2x32+2x1x2+2x1x3−2x2x3,
所以二次型对应的矩阵为
由初等变换得
A→12121−1−112→100−1−3−3233→100−1−30230, 从而
r(A)=2
,于是二次型的秩也为 2。
5
同试卷 1 第 6 题
6
设总体
X
服从正态分布
N(μ1,σ2)
,总体
Y
服从正态分布
N(μ2,σ2)
,
X1,X2,⋯Xn1
和
Y1,Y2,⋯Yn2
分别是来自总体
X
和
Y
的简单随机样本,则
E[n1+n2−2∑i=1n1(Xi−X)2+∑j=1n2(Yj−Y)2]=
【答案】
σ2
【解析】
E[n1−11i=1∑n1(Xi−X)2]=D(X)=σ2,E[n2−11i=1∑n1(Yi−Y)2]=D(Y)=σ2,
所以有
E[i=1∑n1(Xi−X)2]=(n1−1)σ2,E[i=1∑n1(Yi−Y)2]=(n2−1)σ2.
从而
原式=n1+n2−21{E[i=1∑n1(Xi−X)2]+E[j=1∑n2(Yj−Y)2]}
=n1+n2−21[(n1−1)σ2+(n2−1)σ2]=σ2.
选择题
7~14小题,每小题4分,共32分
7
函数
f(x)=x(x−1)(x−2)2∣x∣sin(x−2)
在下列哪个区间内有界
正确答案:A【解析】
如果
f(x)
在
(a,b)
内连续,且极限
limx→a+f(x)
与
limx→b−f(x)
存在,则函数
f(x)
在
(a,b)
内有界。因为
x→−1+limf(x)=x→−1+limx(x−1)(x−2)2−xsin(x−2)=−18sin3,
x→0−limf(x)=x→0−limx(x−1)(x−2)2−xsin(x−2)=−4sin2,
x→0+limf(x)=x→0+limx(x−1)(x−2)2xsin(x−2)=4sin2,
x→1limf(x)=x→1limx(x−1)(x−2)2xsin(x−2)=∞,
x→2limf(x)=x→2limx(x−1)(x−2)2xsin(x−2)=∞
所以函数
f(x)
在
(−1,0)
内有界,故选 (A)。
8
设
f(x)
在
(−∞,+∞)
内有定义,且
limx→∞f(x)=a
,
g(x)={f(x1),0,x=0;x=0.
则
正确答案:D【解析】
由题意可知,
limx→∞f(x)=a
通常是指
x→+∞
时的极限。
当
x→0+
时,
x1→+∞
,因此
x→0+limg(x)=x→0+limf(x1)=a.
当
x→0−
时,
x1→−∞
,但题目并未给出
f(x)
在
x→−∞
时的极限,所以
limx→0−g(x)
可能不存在,也可能存在但不等于
a
。
函数值
g(0)=0
。
- 若
a=0
,则右极限
a=0
,与
g(0)=0
不相等,因此
g(x)
在
x=0
处不连续。
- 若
a=0
,则右极限为 0,但左极限取决于
f(x)
在
−∞
处的行为,此时
g(x)
可能连续,也可能不连续。
综上,
g(x)
在点
x=0
处的连续性与
a
的取值有关。选项 A、B、C 均不一定成立,故正确答案为 D。
9
同试卷 2 第 8 题
10
设有下列命题:
① 若
∑n=1∞(u2n−1+u2n)
收敛,则
∑n=1∞un
收敛.
② 若
∑n=1∞un
收敛,则
∑n=1∞un+1000
收敛.
③ 若
limn→∞unun+1>1
,则
∑n=1∞un
发散.
④ 若
∑n=1∞(un+vn)
收敛,则
∑n=1∞un
,
∑n=1∞vn
都收敛.
则以下命题中正确的是
正确答案:B【解析】
对于命题①,考虑反例:设
un=(−1)n
,则
n=1∑∞(u2n−1+u2n)=n=1∑∞(−1+1)=0
收敛,但
n=1∑∞un=n=1∑∞(−1)n
发散。因此命题①错误。
对于命题②,若
∑n=1∞un
收敛,则去掉前 1000 项后的级数
∑n=1∞un+1000
也收敛,因为级数的收敛性取决于尾部,去掉有限项不改变收敛性。因此命题②正确。
对于命题③,若
n→∞limunun+1>1,
则当
n
足够大时,
∣un∣
不趋于零,实际上会趋于无穷,因此级数
∑n=1∞un
发散。这是比值判别法的结论,命题③正确。
对于命题④,考虑反例:设
un=n
,
vn=−n
,则
n=1∑∞(un+vn)=n=1∑∞0=0
收敛,但
∑n=1∞un
和
∑n=1∞vn
均发散。因此命题④错误。
综上,正确命题为②和③,对应选项 B。
11
设
f′(x)
在
[a,b]
上连续,且
f′(a)>0,f′(b)<0
,则下列结论中错误的是
正确答案:D【解析】
由导数的定义
f′(a)=limx→a+x−af(x)−f(a)>0
,根据极限的保号性,存在
x0∈(a,b)
使得
x0−af(x0)−f(a)>0
,即
f(x0)>f(a)
,所以选项 (A) 正确。
同理,
f′(b)=limx→b−b−xf(b)−f(x)<0
,根据极限的保号性,存在
x0∈(a,b)
使得
f(x0)>f(b)
,所以选项 (B) 正确。
由已知
f′(x)
在
[a,b]
上连续,且
f′(a)>0
,
f′(b)<0
,则由介值定理,存在
x0∈(a,b)
,使得
f′(x0)=0
,所以选项 (C) 正确。
令
f(x)=4−x2
(
−1≤x≤1
),则
f′(−1)=2>0
,
f′(1)=−2<0
,但在
[−1,1]
上
f(x)≥3>0
,所以选项 (D) 是错误的。
12
设
n
阶矩阵
A
与
B
等价,则必有
正确答案:D【解析】
矩阵
A
与
B
等价意味着存在可逆矩阵
P
和
Q
,使得
B=PAQ
等价矩阵具有相同的秩,但行列式不一定相同。
当
∣A∣=0
时,
A
的秩小于
n
,因此
B
的秩也小于
n
,从而
∣B∣=0
。
选项 A 和 B 错误,因为当
∣A∣=0
时,
∣B∣
不一定等于
∣A∣
或
−∣A∣
,可能因初等变换而改变。
选项 C 错误,因为当
∣A∣=0
时,
A
满秩,
B
也满秩,故
∣B∣=0
。
因此,正确选项是 D。
13
设
n
阶矩阵
A
的伴随矩阵
A∗=0,
若
ξ1,ξ2,ξ3,ξ4
是非齐次线性方程组
Ax=b
的互不相等的解,则对应的齐次线性方程组
Ax=0
的基础解系
正确答案:B【解析】
因为
r(A∗)=⎩⎨⎧0,1,n,r(A)<n−1,r(A)=n−1,r(A)=n, 所以由
A∗=0
,可得
r(A)=n−1
或
r(A)=n
。由
ξ1,ξ2
是
Ax=b
的不同的解,得
ξ1−ξ2=0
是
Ax=0
的解,从而
r(A)<n
,因此
r(A)=n−1
。故基础解系所含向量个数为
n−(n−1)=1
。
14
同试卷 1 第 13 题
解答题
15~23小题,共94分
15
(本题满分 8 分)
求
limx→0(sin2x1−x2cos2x)
.
【答案】
34
【解析】
由等价无穷小量代换和洛必达法则,可得
x→0lim(sin2x1−x2cos2x)=x→0limx2sin2xx2−sin2xcos2x=x→0limx4x2−sin2xcos2x=x→0limx4x2−41sin22x=x→0lim4x32x−21sin4x=x→0lim6x21−cos4x=x→0lim6x221(4x)2=34.
16
(本题满分 8 分)
求
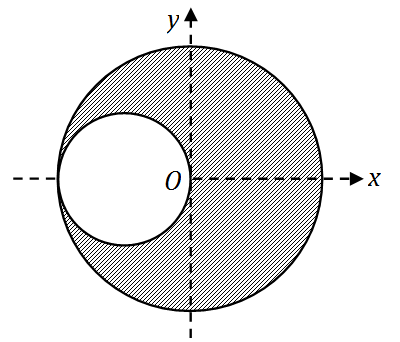
∬D(x2+y2+y)dσ
,
其中
D
是由圆
x2+y2=4
和
(x+1)2+y2=1
所围成的平面区域(如图所示).
【答案】
916(3π−2)
【解析】
首先,积分区域
D
是由圆
x2+y2=4
和
(x+1)2+y2=1
所围成的区域,即大圆内部且小圆外部的区域。由于区域
D
关于
x
轴对称,且被积函数中的
y
是关于
x
轴的奇函数,因此
∬Dydσ=0
。于是,
∬D(x2+y2+y)dσ=∬Dx2+y2dσ. 在极坐标变换
x=rcosθ
,
y=rsinθ
下,有
x2+y2=r
,面积元素
dσ=rdrdθ
,所以
∬Dx2+y2dσ=∬Dr⋅rdrdθ=∬Dr2drdθ. 因此,原积分化为
I=∬Dr2drdθ.
由于
D
是大圆内部且小圆外部的区域,故
∬Dr2drdθ=∬x2+y2≤4r2drdθ−∬(x+1)2+y2≤1r2drdθ.
计算第一个积分:
A=∬x2+y2≤4r2drdθ=∫02π∫02r2drdθ=∫02π[3r3]02dθ=∫02π38dθ=316π.
计算第二个积分。小圆
(x+1)2+y2≤1
在极坐标下表示为
r≤−2cosθ
,其中
θ∈[π/2,3π/2]
,因此
B=∬(x+1)2+y2≤1r2drdθ=∫π/23π/2∫0−2cosθr2drdθ=∫π/23π/2[3r3]0−2cosθdθ=∫π/23π/23−8cos3θdθ.
计算
∫π/23π/2cos3θdθ
:
∫cos3θdθ=∫cosθ(1−sin2θ)dθ=sinθ−31sin3θ+C,
所以
∫π/23π/2cos3θdθ=[sinθ−31sin3θ]π/23π/2=(−1+31)−(1−31)=−32−32=−34.
于是,
B=3−8⋅(−34)=932.
因此,
I=A−B=316π−932=948π−32=916(3π−2).
故所求积分为
916(3π−2)
。
17
(本题满分 8 分)
设
f(x)
,
g(x)
在
[a,b]
上连续,且满足
∫axf(t)dt≥∫axg(t)dt,x∈[a,b),∫abf(t)dt=∫abg(t)dt.
证明:
∫abxf(x)dx≤∫abxg(x)dx
.
【答案】 见解析
【解析】
设
h(x)=f(x)−g(x)
,则由条件可得
∫axh(t)dt≥0,x∈[a,b),∫abh(t)dt=0.
令
H(x)=∫axh(t)dt
,则
H(x)≥0
对于
x∈[a,b)
,且
H(b)=0
。
考虑积分
∫abxh(x)dx=∫abxdH(x).
使用分部积分法:
∫abxdH(x)=[xH(x)]ab−∫abH(x)dx.
由于
H(a)=0
和
H(b)=0
,故
[xH(x)]ab=0,
因此
∫abxh(x)dx=−∫abH(x)dx.
由于
H(x)≥0
在
[a,b]
上,且
H(x)
连续,故
∫abH(x)dx≥0,
所以
∫abxh(x)dx≤0,
即
∫abxf(x)dx−∫abxg(x)dx≤0,
从而
∫abxf(x)dx≤∫abxg(x)dx.
证毕。
18
(本题满分 9 分)
设某商品的需求函数为
Q=100−5P
,其中价格
P∈(0,20)
,
Q
为需求量.
(1) 求需求量对价格的弹性
Ed
(
Ed
> 0);
(2) 推导
dPdR=Q(1−Ed)
(其中
R
为收益),
并用弹性
Ed
说明价格在何范围内变化时,降低价格反而使收益增加.
【答案】
(1)
Ed=20−PP
(2) 当
P∈(10,20)
时,降低价格反而使收益增加。
【解析】
(I) 由于需求量对价格的弹性
Ed>0
,所以
Ed=QPdPdQ=100−5PP⋅(−5)=20−PP. (II) 由
R=PQ
,得
dPdR=Q+PdPdQ=Q(1+QPdPdQ)=Q(1+20−P−P)=Q(1−Ed).
令
dPdR<0
,可得
Ed>1
,即
20−PP>1
,解得
P>10
。又已知
P∈(0,20)
,所以当
10<P<20
时,收益随价格降低反而增加。
19
(本题满分 9 分)
设级数
2⋅4x4+2⋅4⋅6x6+2⋅4⋅6⋅8x8+⋯(−∞<x<+∞)
的和函数为
S(x)
.求:
(1)
S(x)
所满足的一阶微分方程;
(2)
S(x)
的表达式.
【答案】
(1)
S(x)
所满足的一阶微分方程为:
S′(x)−xS(x)=2x3
(2)
S(x)
的表达式为:
S(x)=e2x2−1−2x2
【解析】
(I) 易知
S(0)=0
,且有
S′(x)=2x3+2⋅4x5+2⋅4⋅6x7+⋯
=x(2x2+2⋅4x4+2⋅4⋅6x6+⋯)=x[2x2+S(x)].
因此
S(x)
满足一阶线性微分方程及相应的初始条件:
S′(x)−xS(x)=2x3,S(0)=0.
(II) 由通解公式,上述微分方程的通解为
S(x)=e∫xdx(∫2x3e−∫xdxdx+C)=e2x2(∫2x3e−2x2dx+C)=e2x2(−∫2x2d(e−2x2)+C)=e2x2(−2x2e−2x2+∫e−2x2d(2x2)+C)=−2x2−e2x2⋅e−2x2+Ce2x2=−2x2−1+Ce2x2.
由初始条件
S(0)=0
,得
C=1
。故
S(x)=−2x2−1+e2x2.
20
(本题满分 13 分)
设
α1=(1,2,0)T
,
α2=(1,α+2,−3α)T
,
α3=(−1,−b−2,α+2b)T
,
β=(1,3,−3)T
,试讨论当
a,b
为何值时,
(1)
β
不能由
α1,α2,α3
线性表示;
(2)
β
可由
α1,α2,α3
唯一地线性表示,并求出表示式;
(3)
β
可由
α1,α2,α3
线性表示,但表示式不唯一,并求出表示式.
【答案】
(1) 当
a=0
时,
β
不能由
α1,α2,α3
线性表示。
(2) 当
a=0
且
a=b
时,
β
可由
α1,α2,α3
唯一地线性表示,表示式为:
β=(1−a1)α1+a1α2
(3) 当
a=0
且
a=b
时,
β
可由
α1,α2,α3
线性表示,但表示式不唯一,表示式为:
β=(1−a1)α1+(a1+k)α2+kα3
其中
k
为任意常数。
【解析】
设存在实数
x1,x2,x3
使得方程组
α1x1+α2x2+α3x3=β
成立。记
A=(α1,α2,α3)
,对矩阵
(A,β)
作初等行变换得
(A,β)=1201a+2−3a−1−b−2a+2b13−3→1001a0−1−ba−b110. (I) 当
a=0
时,由
(A,β)→100100−1−b−b110. 可知
r(A)=r(A,β)
。故方程组无解,即
β
不能由
α1,α2,α3
线性表示。
(II) 当
a=0
且
a=b
时,可知
r(A)=r(A,β)=3
,故方程组有唯一解。由同解阶梯形方程求解得
x1=1−a1,x2=a1,x3=0.
此时
β
可由
α1,α2,α3
唯一地线性表示,其表示式为
β=(1−a1)α1+a1α2.
(III) 当
a=0
且
a=b=0
时,对矩阵
(A,β)
继续作初等行变换得
(A,β)→1001a0−1−a0110→100110−1−101a10→1000100−101−a1a10. 从而
r(A)=r(A,β)=2
。故方程组有无穷多解,其全部解为
x1=1−a1,x2=a1+c,x3=c,
其中
c
为任意常数。此时
β
可由
α1,α2,α3
线性表示,但表示式不唯一,其表示式为
β=(1−a1)α1+(a1+c)α2+cα3.
21
(本题满分 13 分)
设
n
阶矩阵
A=1b⋮bb1⋮b⋯⋯⋯bb⋮1
.
(1) 求
A
的特征值和特征向量;
(2) 求可逆矩阵
P
,使得
P−1AP
为对角矩阵.
【答案】 见解析
【解析】
(Ⅰ) 当
b=0
时,
∣λE−A∣=λ−1−b⋮−b−bλ−1⋮−b⋯⋯⋱⋯−b−b⋮λ−1=[λ−1−(n−1)b][λ−(1−b)]n−1. 故
A
的特征值为
λ1=1+(n−1)b
,
λ2=⋯=λn=1−b
。对
λ1=1+(n−1)b
,
λ1E−A=(n−1)b−b⋮−b−b(n−1)b⋮−b⋯⋯⋱⋯−b−b⋮(n−1)b→10⋮0001⋮00⋯⋯⋱⋯⋯00⋮10−1−1⋮−10 求得基础解系
ξ1=(1,1,1,⋯,1)T
,所以
A
的属于
λ1
的全部特征向量为
kξ1=k(1,1,1,⋯,1)T
(
k
为任意不为零的常数)。
对
λ2=⋯=λn=1−b
,
λiE−A=−b−b⋮−b−b−b⋮−b⋯⋯⋱⋯−b−b⋮−b→10⋮010⋮0⋯⋯⋱⋯10⋮0 求得基础解系为
ξ2=(1,−1,0,⋯,0)T,ξ3=(1,0,−1,⋯,0)T,⋯,ξn=(1,0,0,⋯,−1)T.
故
A
的属于
λ2=⋯=λn
的全部特征向量为
k2ξ2+k3ξ3+⋯+knξn
(
k2,k3,⋯,kn
是不全为零的常数)。
当
b=0
时,
∣λE−A∣=λ−10⋮00λ−1⋮0⋯⋯⋱⋯00⋮λ−1=(λ−1)n, 特征值为
λ1=⋯=λn=1
,任意非零列向量均为特征向量。
(Ⅱ) 当
b=0
时,
A
有
n
个线性无关的特征向量。令
P=(ξ1,ξ2,⋯,ξn)
,则
P−1AP=1+(n−1)b1−b⋱1−b. 当
b=0
时,
A=E
,对任意可逆矩阵
P
,均有
P−1AP=E
。
22
(本题满分 13 分)
设
A
,
B
为随机事件,且
P(A)=41
,
P(B∣A)=31
,
P(A∣B)=21
.令
X={1,0,A发生,A不发生;Y={1,0,B发生,B不发生.
求:
(1) 二维随机变量
(X,Y)
的概率分布;
(2)
X
和
Y
的相关系数
ρXY
;
(3)
Z=X2+Y2
的概率分布.
【答案】
(1) 二维随机变量
(X,Y)
的概率分布为:
X=0X=1Y=03261Y=1121121
(2)
X
和
Y
的相关系数
ρXY=151
。
(3)
Z=X2+Y2
的概率分布为:
ZP0321412121
【解析】
(I) 由于
P(AB)=P(A)P(B∣A)=121
,所以
P(B)=P(A∣B)P(AB)=61
。利用条件概率公式和事件间简单的运算关系,有
P{X=1,Y=1}=P(AB)=121,
P{X=1,Y=0}=P(ABˉ)=P(A)−P(AB)=61,
P{X=0,Y=1}=P(AˉB)=P(B)−P(AB)=121,
P{X=0,Y=0}=P(AˉBˉ)=1−P(A+B)=1−P(A)−P(B)+P(AB)=32.
故
(X,Y)
的概率分布为
X=0X=1Y=03261Y=1121121
(II)
X,Y
的概率分布分别为
P{X=0}=P{X=0,Y=1}+P{X=0,Y=0}=32+121=43,
P{X=1}=P{X=1,Y=1}+P{X=1,Y=0}=61+121=41,
P{Y=0}=P{X=0,Y=0}+P{X=1,Y=0}=32+61=65,
P{Y=1}=P{X=0,Y=1}+P{X=1,Y=1}=121+121=61.
所以
X,Y
的概率分布为
XP043141YP065161
由 0-1 分布的数学期望和方差公式,有
EX=41,EY=61,DX=41×43=163,DY=61×65=365,
E(XY)=0⋅P{XY=0}+1⋅P{XY=1}=P{X=1,Y=1}=121.
故协方差和相关系数等于
Cov(X,Y)=E(XY)−EX⋅EY=241,ρXY=DX⋅DYCov(X,Y)=1515. (III)
Z
的可能取值为 0, 1, 2. 且有
P{Z=0}=P{X=0,Y=0}=32,
P{Z=1}=P{X=1,Y=0}+P{X=0,Y=1}=41
P{Z=2}=P{X=1,Y=1}=121.
即
Z
的概率分布为
ZP0321412121
23
(本题满分 13 分)
设随机变量
X
的分布函数为
F(x;α,β)={1−(xα)β,0,x>α,x≤α,
其中参数
α>0,β>1
.设
X1,X2,⋯,Xn
为来自总体
X
的简单随机样本,
(1) 当
α=1
时,求未知参数
β
的矩估计量;
(2) 当
α=1
时,求未知参数
β
的最大似然估计量;
(3) 当
β=2
时,求未知参数
α
的最大似然估计量.
【答案】
(1)
β^=Xˉ−1Xˉ
(2)
β^=∑i=1nlnXin
(3)
α^=min{X1,X2,⋯,Xn}
【解析】
当
a=1
时,
X
的概率密度为
f(x,β)=⎩⎨⎧xβ+1β,0,x>1;x≤1. (I) 由数学期望的定义:
EX=∫−∞+∞xf(x;β)dx=∫1+∞x⋅xβ+1βdx=β−1β.
用样本均值估计期望有
EX=X
,即
β−1β=X
,解得
β=X−1X
,所以参数
β
的矩估计量为
β^=X−1X,其中 X=n1i=1∑nXi.
(II) 设
x1,x2,⋯,xn
是相应于样本
X1,X2,⋯,Xn
的一组观测值,则似然函数为
L(β)=i=1∏nf(xi;β)=⎩⎨⎧(x1x2⋯xn)β+1βn,0,xi>1 (i=1,2,⋯,n),其他. 当
xi>1 (i=1,2,⋯,n)
时,
L(β)>0
,取自然对数得
lnL(β)=nlnβ−(β+1)i=1∑nlnxi.
两边对
β
求导,并令导数为零得
dβdlnL(β)=βn−i=1∑nlnxi=0⇒β=∑i=1nlnxin.
从而
β
的最大似然估计量为
β^=i=1∑nlnXin
。
(Ⅲ) 当
β=2
时,
X
的概率密度为
f(x,β)=⎩⎨⎧x32α2,0,x>α;x≤α. 对于总体
X
的样本值
x1,x2,⋯,xn
,似然函数为
L(α)=i=1∏nf(xi;α)=⎩⎨⎧(x1x2⋯xn)32nα2n,0,xi>α (i=1,2,⋯,n),其他. 当
xi>α
(
i=1,2,⋯,n
) 时,
α
越大,
L(α)
越大。但是必须满足条件
α≤xi
(
i=1,2,⋯,n
),所以
α
的最大似然估计值为
α^=min{x1,x2,⋯,xn}
。于是
α
的最大似然估计量为
α^=min{X1,X2,⋯,Xn}
。