卷 1

填空题

1～6小题，每小题4分，共24分

1

曲线 $y = \frac{x^2}{2x + 1}$ 的斜渐近线方程为 ______．

【答案】
$y = \frac{1}{2} x - \frac{1}{4}$

【解析】
曲线 $y = \frac{x^2}{2x + 1}$ 的斜渐近线形式为 $y = mx + b$ 。
首先求斜率 $m$ ：

m = \lim_{x \to \infty} \frac{y}{x} = \lim_{x \to \infty} \frac{\frac{x^2}{2x + 1}}{x} = \lim_{x \to \infty} \frac{x}{2x + 1} = \lim_{x \to \infty} \frac{1}{2 + \frac{1}{x}} = \frac{1}{2}

然后求截距 $b$ ：

b = \lim_{x \to \infty} (y - mx) = \lim_{x \to \infty} \left( \frac{x^2}{2x + 1} - \frac{1}{2} x \right) = \lim_{x \to \infty} \frac{2x^2 - x(2x + 1)}{2(2x + 1)} = \lim_{x \to \infty} \frac{-x}{4x + 2} = \lim_{x \to \infty} \frac{-1}{4 + \frac{2}{x}} = -\frac{1}{4}

因此，斜渐近线方程为 $y = \frac{1}{2} x - \frac{1}{4}$ 。

2

微分方程 $xy' + 2y = x\ln x$ 满足 $y(1) = - \frac{1}{9}$ 的解为 ______．

高等数学常微分方程一阶非齐次线性微分方程

【答案】
$y = \frac{x}{3} \ln x - \frac{x}{9}$

【解析】
给定微分方程 $xy' + 2y = x\ln x$ 和初始条件 $y(1) = -\frac{1}{9}$ 。
首先，将方程化为标准形式 $y' + P(x)y = Q(x)$ ，即

y' + \frac{2}{x}y = \ln x

其中 $P(x) = \frac{2}{x}$ ， $Q(x) = \ln x$ 。
计算积分因子 $\mu(x) = e^{\int P(x) \, dx} = e^{\int \frac{2}{x} \, dx} = e^{2\ln x} = x^2$ 。
将原方程乘以积分因子：

x^2 y' + 2x y = x^2 \ln x

左边可写为 $\frac{d}{dx}(x^2 y)$ ，因此

\frac{d}{dx}(x^2 y) = x^2 \ln x

两边积分：

x^2 y = \int x^2 \ln x \, dx

计算积分：
设 $u = \ln x$ ， $dv = x^2 \, dx$ ，则 $du = \frac{1}{x} dx$ ， $v = \frac{x^3}{3}$ ，

\int x^2 \ln x \, dx = \frac{x^3}{3} \ln x - \int \frac{x^3}{3} \cdot \frac{1}{x} dx = \frac{x^3}{3} \ln x - \frac{1}{3} \int x^2 \, dx = \frac{x^3}{3} \ln x - \frac{1}{3} \cdot \frac{x^3}{3} = \frac{x^3}{3} \ln x - \frac{x^3}{9}

所以

x^2 y = \frac{x^3}{3} \ln x - \frac{x^3}{9} + C

解得

y = \frac{x}{3} \ln x - \frac{x}{9} + \frac{C}{x^2}

代入初始条件 $y(1) = -\frac{1}{9}$ ：

-\frac{1}{9} = \frac{1}{3} \ln 1 - \frac{1}{9} + C

由于 $\ln 1 = 0$ ，有

-\frac{1}{9} = 0 - \frac{1}{9} + C

解得 $C = 0$ 。
因此，解为

y = \frac{x}{3} \ln x - \frac{x}{9}

3

设函数 $u(x,y,z) = 1 + \frac{x^2}{6} + \frac{y^2}{12} + \frac{z^2}{18}$ ，单位向量 $\vec{n} = \frac{1}{\sqrt{3}}\{1,1,1\}$ ，则 $\frac{\pdu}{\pdn}\big|_{(1,2,3)} =$ ______．

高等数学多元函数微分学方向导数和梯度

【答案】 $\frac{1}{\sqrt{3}}$

【解析】 函数 $u(x,y,z) = 1 + \frac{x^2}{6} + \frac{y^2}{12} + \frac{z^2}{18}$ 在点 $(1,2,3)$ 处沿单位向量 $\vec{n} = \frac{1}{\sqrt{3}}(1,1,1)$ 的方向导数 $\frac{\partial u}{\partial n}$ 由梯度 $\nabla u$ 与 $\vec{n}$ 的点积给出。

首先计算梯度 $\nabla u$ ：

\frac{\partial u}{\partial x} = \frac{x}{3}, \quad \frac{\partial u}{\partial y} = \frac{y}{6}, \quad \frac{\partial u}{\partial z} = \frac{z}{9}

因此，

\nabla u = \left( \frac{x}{3}, \frac{y}{6}, \frac{z}{9} \right)

在点 $(1,2,3)$ 处，

\nabla u|_{(1,2,3)} = \left( \frac{1}{3}, \frac{2}{6}, \frac{3}{9} \right) = \left( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right)

然后计算点积：

\frac{\partial u}{\partial n} = \nabla u \cdot \vec{n} = \left( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right) \cdot \frac{1}{\sqrt{3}}(1,1,1) = \frac{1}{3} \cdot \frac{1}{\sqrt{3}} + \frac{1}{3} \cdot \frac{1}{\sqrt{3}} + \frac{1}{3} \cdot \frac{1}{\sqrt{3}} = 3 \cdot \frac{1}{3} \cdot \frac{1}{\sqrt{3}} = \frac{1}{\sqrt{3}}

故方向导数为 $\frac{1}{\sqrt{3}}$ 。

4

设 $\Omega$ 是由锥面 $z = \sqrt{x^2 + y^2}$ 与半球面 $z = \sqrt{R^2 - x^2 - y^2}$ 围成的空间区域， $\Sigma$ 是 $\Omega$ 的整个边界的外侧，则 $\iint_{\Sigma}x\dy\dz + y\dz\dx + z\dx\dy =$ ______．

高等数学多元函数积分学第二类曲面积分

【答案】 $\pi R^3 (2 - \sqrt{2})$

【解析】 根据高斯公式，将曲面积分转化为体积分：

\iint_{\Sigma} x \, dy \, dz + y \, dz \, dx + z \, dx \, dy = \iiint_{\Omega} \left( \frac{\partial x}{\partial x} + \frac{\partial y}{\partial y} + \frac{\partial z}{\partial z} \right) dV = \iiint_{\Omega} 3 \, dV = 3 \iiint_{\Omega} dV.

其中， $\Omega$ 是由锥面 $z = \sqrt{x^2 + y^2}$ 与半球面 $z = \sqrt{R^2 - x^2 - y^2}$ 围成的区域。计算区域 $\Omega$ 的体积，使用柱坐标变换：

x = r \cos \theta, \quad y = r \sin \theta, \quad z = z, \quad dV = r \, dr \, d\theta \, dz.

锥面与半球面相交于 $x^2 + y^2 = \frac{R^2}{2}$ ，即 $r = \frac{R}{\sqrt{2}}$ 。对于 $r \in [0, \frac{R}{\sqrt{2}}]$ ， $z$ 从锥面 $z = r$ 到半球面 $z = \sqrt{R^2 - r^2}$ 。体积分为：

\iiint_{\Omega} dV = \int_{0}^{2\pi} d\theta \int_{0}^{\frac{R}{\sqrt{2}}} r \, dr \int_{r}^{\sqrt{R^2 - r^2}} dz = \int_{0}^{2\pi} d\theta \int_{0}^{\frac{R}{\sqrt{2}}} r \left( \sqrt{R^2 - r^2} - r \right) dr.

计算径向积分：

\int_{0}^{\frac{R}{\sqrt{2}}} r \sqrt{R^2 - r^2} \, dr = \frac{R^3}{3} \left(1 - \frac{1}{2^{3/2}}\right), \quad \int_{0}^{\frac{R}{\sqrt{2}}} r^2 \, dr = \frac{R^3}{3 \cdot 2^{3/2}}.

所以，

\int_{0}^{\frac{R}{\sqrt{2}}} r \left( \sqrt{R^2 - r^2} - r \right) dr = \frac{R^3}{3} \left(1 - \frac{1}{2^{3/2}} - \frac{1}{2^{3/2}}\right) = \frac{R^3}{3} \left(1 - \frac{1}{\sqrt{2}}\right).

因此，

\iiint_{\Omega} dV = 2\pi \cdot \frac{R^3}{3} \left(1 - \frac{1}{\sqrt{2}}\right) = \frac{2\pi R^3}{3} \left(1 - \frac{1}{\sqrt{2}}\right).

曲面积分为：

3 \cdot \frac{2\pi R^3}{3} \left(1 - \frac{1}{\sqrt{2}}\right) = 2\pi R^3 \left(1 - \frac{1}{\sqrt{2}}\right) = \pi R^3 (2 - \sqrt{2}).

故答案为 $\pi R^3 (2 - \sqrt{2})$ 。

5

设 $\alpha_1,\alpha_2,\alpha_3$ 均为3维列向量，记矩阵

A = (\alpha_1,\alpha_2,\alpha_3),\quad B = (\alpha_1 + \alpha_2 + \alpha_3,\alpha_1 + 2\alpha_2 + 4\alpha_3,\alpha_1 + 3\alpha_2 + 9\alpha_3),

如果 $|A| = 1$ ，那么 $|B| =$ ______．

线性代数矩阵伴随矩阵与可逆矩阵

【答案】 2

【解析】 已知矩阵 $A = (\alpha_1, \alpha_2, \alpha_3)$ 且 $|A| = 1$ ，矩阵 $B = (\alpha_1 + \alpha_2 + \alpha_3, \alpha_1 + 2\alpha_2 + 4\alpha_3, \alpha_1 + 3\alpha_2 + 9\alpha_3)$ 。
将 $B$ 表示为 $B = A C$ ，其中 $C$ 是一个系数矩阵。
通过分析 $B$ 的列向量：

第一列 $\alpha_1 + \alpha_2 + \alpha_3 = A \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$ ，
第二列 $\alpha_1 + 2\alpha_2 + 4\alpha_3 = A \begin{pmatrix} 1 \\ 2 \\ 4 \end{pmatrix}$ ，
第三列 $\alpha_1 + 3\alpha_2 + 9\alpha_3 = A \begin{pmatrix} 1 \\ 3 \\ 9 \end{pmatrix}$ ，
因此 $C = \begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{pmatrix}$ 。
于是 $|B| = |A| \cdot |C| = 1 \cdot |C|$ 。
计算 $|C|$ ：
$|C| = \begin{vmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{vmatrix} = 1 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 9 \end{vmatrix} - 1 \cdot \begin{vmatrix} 1 & 3 \\ 1 & 9 \end{vmatrix} + 1 \cdot \begin{vmatrix} 1 & 2 \\ 1 & 4 \end{vmatrix} = 1 \cdot (18-12) - 1 \cdot (9-3) + 1 \cdot (4-2) = 6 - 6 + 2 = 2.$ 或者， $C$ 是范德蒙德矩阵，节点为 $1, 2, 3$ ，其行列式为 $(2-1)(3-1)(3-2) = 1 \times 2 \times 1 = 2$ 。
故 $|B| = 2$ 。

6

从数 $1$ , $2$ , $3$ , $4$ 中任取一个数，记为 $X$ ，再从 $1,2, \cdots ,X$ 中任取一个数，记为 $Y$ ，则 $P\{Y = 2\} =$ ______．

概率论与数理统计随机事件和概率

【答案】 $\dfrac{13}{48}$

【解析】 首先， $X$ 从集合 $\{1, 2, 3, 4\}$ 中等概率取值的概率为 $P\{X = i\} = \dfrac{1}{4}$ ，其中 $i = 1, 2, 3, 4$ 。
然后，在给定 $X$ 的条件下， $Y$ 从集合 $\{1, 2, \cdots, X\}$ 中等概率取值。
因此， $P\{Y = 2 \mid X = i\}$ 取决于 $i$ ：

当 $X = 1$ 时， $Y$ 只能取 1，故 $P\{Y = 2 \mid X = 1\} = 0$ ；
当 $X = 2$ 时， $Y$ 从 $\{1, 2\}$ 中取，故 $P\{Y = 2 \mid X = 2\} = \dfrac{1}{2}$ ；
当 $X = 3$ 时， $Y$ 从 $\{1, 2, 3\}$ 中取，故 $P\{Y = 2 \mid X = 3\} = \dfrac{1}{3}$ ；
当 $X = 4$ 时， $Y$ 从 $\{1, 2, 3, 4\}$ 中取，故 $P\{Y = 2 \mid X = 4\} = \dfrac{1}{4}$ 。
由全概率公式：
$P\{Y = 2\} = \sum_{i=1}^{4} P\{X = i\} \cdot P\{Y = 2 \mid X = i\}$ 代入计算：
$P\{Y = 2\} = \frac{1}{4} \times 0 + \frac{1}{4} \times \frac{1}{2} + \frac{1}{4} \times \frac{1}{3} + \frac{1}{4} \times \frac{1}{4} = \frac{1}{4} \left( 0 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} \right)$ 计算括号内和：
$\frac{1}{2} + \frac{1}{3} + \frac{1}{4} = \frac{6}{12} + \frac{4}{12} + \frac{3}{12} = \frac{13}{12}$ 所以：
$P\{Y = 2\} = \frac{1}{4} \times \frac{13}{12} = \frac{13}{48}$ 因此，答案为 $\dfrac{13}{48}$ 。

选择题

7～14小题，每小题4分，共32分

7

设函数 $f(x) = \lim_{n \to \infty} \sqrt[n]{1+|x|^{3n}}$ ，则 $f(x)$ 在 $(-\infty , +\infty)$ 内

高等数学函数、极限、连续函数极限的计算

正确答案：C

【解析】
函数 $f(x) = \lim_{n \to \infty} \sqrt[n]{1 + |x|^{3n}}$ 的极限计算如下：

当 $|x| < 1$ 时， $|x|^{3n} \to 0$ ，故 $f(x) = 1$ 。
当 $|x| = 1$ 时， $1 + |x|^{3n} = 2$ ，故 $f(x) = \lim_{n \to \infty} \sqrt[n]{2} = 1$ 。
当 $|x| > 1$ 时， $|x|^{3n} \to \infty$ ，故 $f(x) = |x|^3$ 。
因此， $f(x) = \begin{cases} 1 & \text{if } |x| \leq 1 \\ |x|^3 & \text{if } |x| > 1 \end{cases}$ 。

由于 $f(x)$ 是偶函数，只需考虑 $x \geq 0$ 时的可导性。

在 $x=0$ 处， $f(x) = 1$ 常数，可导，导数为 0。
在 $x=1$ 处，左导数为 0，右导数为 3，不可导。
由偶函数对称性，在 $x=-1$ 处同样不可导。
在 $|x| < 1$ 且 $x \neq 0$ 时， $f(x) = 1$ 可导；在 $|x| > 1$ 时， $f(x) = |x|^3$ 可导。
因此，不可导点恰为 $x=1$ 和 $x=-1$ ，共两个不可导点。

8

设 $F(x)$ 是连续函数 $f(x)$ 的一个原函数，表示“ $M$ 的充分必要条件是 $N$ ”，则必有

高等数学一元函数积分学定积分的概念、性质及几何意义

正确答案：A

【解析】 设 $F(x)$ 是 $f(x)$ 的一个原函数，即 $F'(x) = f(x)$ 。

对于选项 A：若 $F(x)$ 是偶函数，即 $F(-x) = F(x)$ ，求导得 $-F'(-x) = F'(x)$ ，即 $f(-x) = -f(x)$ ，所以 $f(x)$ 是奇函数；反之，若 $f(x)$ 是奇函数，考虑原函数 $F(x) = \int_0^x f(t) \, dt$ ，则 $F(-x) = \int_0^{-x} f(t) \, dt$ ，令 $u = -t$ ，得 $F(-x) = \int_0^x f(-u) \, (-du) = \int_0^x -f(u) \, (-du) = \int_0^x f(u) \, du = F(x)$ ，所以 $F(x)$ 是偶函数，且任意原函数 $F(x) + C$ 也是偶函数。因此 $F(x)$ 是偶函数 $\Leftrightarrow$ $f(x)$ 是奇函数，选项 A 正确。
对于选项 B：若 $F(x)$ 是奇函数，则 $F(-x) = -F(x)$ ，求导得 $-F'(-x) = -F'(x)$ ，即 $f(-x) = f(x)$ ，所以 $f(x)$ 是偶函数；但若 $f(x)$ 是偶函数，原函数 $F(x) = \int_0^x f(t) \, dt$ 是奇函数，但其他原函数 $F(x) + C$ 可能不是奇函数（当 $C \neq 0$ ），因此 $\Leftrightarrow$ 不成立。
对于选项 C：若 $F(x)$ 是周期函数，则 $F(x+T) = F(x)$ ，求导得 $f(x+T) = f(x)$ ，所以 $f(x)$ 是周期函数；但若 $f(x)$ 是周期函数，原函数 $F(x) = \int_0^x f(t) \, dt$ 满足 $F(x+T) = F(x) + \int_0^T f(t) \, dt$ ，当 $\int_0^T f(t) \, dt \neq 0$ 时 $F(x)$ 不是周期函数，因此 $\Leftrightarrow$ 不成立。
对于选项 D：若 $F(x)$ 是单调函数，则 $f(x) = F'(x) \geq 0$ （或 $\leq 0$ )，但 $f(x)$ 不一定单调；反之，若 $f(x)$ 是单调函数，原函数 $F(x)$ 不一定单调，例如 $f(x) = x$ 单调递增，但原函数 $F(x) = \frac{x^2}{2}$ 在 $(-\infty, 0)$ 递减，在 $(0, \infty)$ 递增，不是单调函数，因此 $\Leftrightarrow$ 不成立。
故正确答案为 A。

9

设函数 $u(x,y) = \phi(x + y) + \phi(x - y) + \int_{x - y}^{x + y} \psi(t)\dt$ ，其中函数 $\phi$ 具有二阶导数， $\psi$ 具有一阶导数，则必有

高等数学多元函数微分学偏导数的概念与计算

正确答案：B

【解析】 给定函数 $u(x,y) = \phi(x + y) + \phi(x - y) + \int_{x - y}^{x + y} \psi(t) \, dt$ ，其中 $\phi$ 具有二阶导数， $\psi$ 具有一阶导数。计算一阶偏导数：

\frac{\partial u}{\partial x} = \phi'(x + y) + \phi'(x - y) + \psi(x + y) - \psi(x - y)

\frac{\partial u}{\partial y} = \phi'(x + y) - \phi'(x - y) + \psi(x + y) + \psi(x - y)

接着计算二阶偏导数：

\frac{\partial^2 u}{\partial x^2} = \phi''(x + y) + \phi''(x - y) + \psi'(x + y) - \psi'(x - y)

\frac{\partial^2 u}{\partial y^2} = \phi''(x + y) + \phi''(x - y) + \psi'(x + y) - \psi'(x - y)

比较得 $\frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 u}{\partial y^2}$ ，故选项 B 正确。其他选项不成立，例如混合偏导数 $\frac{\partial^2 u}{\partial x \partial y} = \phi''(x + y) - \phi''(x - y) + \psi'(x + y) + \psi'(x - y)$ 与 $\frac{\partial^2 u}{\partial x^2}$ 或 $\frac{\partial^2 u}{\partial y^2}$ 均不相等。

10

设有三元方程 $xy - z\ln y + \e^{xz} = 1$ ，根据隐函数存在定理，存在点 $(0,1,1)$ 的一个邻域，在此邻域内该方程

高等数学多元函数微分学偏导数的概念与计算

正确答案：D
【解析】 定义函数

F(x,y,z) = xy - z \ln y + e^{xz} - 1

，在点

(0,1,1)

处，

F(0,1,1) = 0 \cdot 1 - 1 \cdot \ln 1 + e^{0 \cdot 1} - 1 = 0 - 0 + 1 - 1 = 0

，满足隐函数存在定理的条件。计算偏导数：

\frac{\partial F}{\partial x} = y + z e^{xz}

，在

(0,1,1)

处值为

1 + 1 \cdot e^0 = 2 \neq 0

；

\frac{\partial F}{\partial y} = x - \frac{z}{y}

，在

(0,1,1)

处值为

0 - \frac{1}{1} = -1 \neq 0

；

\frac{\partial F}{\partial z} = -\ln y + x e^{xz}

，在

(0,1,1)

处值为

-\ln 1 + 0 \cdot e^0 = 0

。由于

\frac{\partial F}{\partial z} = 0

，不能确定隐函数

z = z(x,y)

；但

\frac{\partial F}{\partial x} \neq 0

和

\frac{\partial F}{\partial y} \neq 0

，因此可以确定隐函数

x = x(y,z)

和

y = y(x,z)

，且它们具有连续偏导数。故选项 D 正确。

11

设 $\lambda_1,\lambda_2$ 是矩阵 $A$ 的两个不同的特征值，对应的特征向量分别为 $\alpha_1,\alpha_2$ ，则 $\alpha_1$ ， $A(\alpha_1 + \alpha_2)$ 线性无关的充分必要条件是

线性代数矩阵的特征值与特征向量

正确答案：B

【解析】
设向量组为 $\alpha_1$ 与 $A(\alpha_1 + \alpha_2)$ 。
已知

A\alpha_1 = \lambda_1\alpha_1,\quad A\alpha_2 = \lambda_2\alpha_2,

所以

A(\alpha_1 + \alpha_2) = \lambda_1\alpha_1 + \lambda_2\alpha_2.

考虑线性组合

c_1\alpha_1 + c_2\bigl(\lambda_1\alpha_1 + \lambda_2\alpha_2\bigr) = 0,

整理得

(c_1 + c_2\lambda_1)\alpha_1 + c_2\lambda_2\alpha_2 = 0.

由于 $\alpha_1$ 与 $\alpha_2$ 属于不同特征值，它们线性无关，因此系数必须全为零：

\begin{cases} c_1 + c_2\lambda_1 = 0, \\ c_2\lambda_2 = 0. \end{cases}

若 $\lambda_2 \neq 0$ ，则 $c_2 = 0$ ，代入第一式得 $c_1 = 0$ ，向量组线性无关。
若 $\lambda_2 = 0$ ，则 $c_2$ 可取任意非零值，如取 $c_2 = 1$ ，则 $c_1 = -\lambda_1$ ，存在非零解，向量组线性相关。

因此，向量组线性无关的充要条件是 $\lambda_2 \neq 0$ ，对应选项 B。

12

设 $A$ 为 $n$ ( $n \ge 2$ )阶可逆矩阵，交换 $A$ 的第 $1$ 行与第 $2$ 行得矩阵 $B$ ， $A^*,B^*$ 分别为 $A$ , $B$ 的伴随矩阵，则

线性代数矩阵伴随矩阵与可逆矩阵

正确答案：C

【解析】 设 $A$ 为 $n$ 阶可逆矩阵，交换 $A$ 的第 $1$ 行与第 $2$ 行得矩阵 $B$ ，即 $B = E_{12} A$ ，其中 $E_{12}$ 为交换两行的初等矩阵。由伴随矩阵的性质， $A^* = |A| A^{-1}$ ， $B^* = |B| B^{-1}$ 。由于交换两行改变行列式的符号，有 $|B| = -|A|$ 。同时， $B^{-1} = A^{-1} E_{12}^{-1} = A^{-1} E_{12}$ （因为 $E_{12}^{-1} = E_{12}$ )。代入得 $B^* = (-|A|) A^{-1} E_{12} = - (|A| A^{-1}) E_{12} = - A^* E_{12}$ 。右乘 $E_{12}$ 表示交换矩阵的列，因此 $A^* E_{12}$ 是交换 $A^*$ 的第 $1$ 列与第 $2$ 列后的矩阵。故 $B^* = - (A^* \text{ } 1 \text{ } 2 \text{ })$ ，即交换 $A^*$ 的第 $1$ 列与第 $2$ 列得 $- B^*$ 。选项 C 正确。

通过 $n=2$ 的例子验证：设 $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ ，则 $A^* = \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$ 。交换行得 $B = \begin{pmatrix} c & d \\ a & b \end{pmatrix}$ ，则 $B^* = \begin{pmatrix} b & -d \\ -a & c \end{pmatrix}$ 。交换 $A^*$ 的第 $1$ 列与第 $2$ 列得 $\begin{pmatrix} -b & d \\ a & -c \end{pmatrix} = - B^*$ ，符合结论。其他选项不成立。

13

设二维随机变量 $(X,Y)$ 的概率分布为

\begin{array}{|c|cc|} \hline X\backslash Y & 0 & 1 \\ \hline 0 & 0.4 & a \\ 1 & b & 0.1 \\ \hline \end{array}

已知随机事件 $\{X = 0\}$ 与 $\{X + Y = 1\}$ 相互独立，则

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

正确答案：B

【解析】
由概率分布的性质，所有概率之和为 1，即

0.4 + a + b + 0.1 = 1,

解得

a + b = 0.5.

事件 $\{X=0\}$ 与 $\{X+Y=1\}$ 相互独立，因此

P(\{X=0\} \cap \{X+Y=1\}) = P(\{X=0\}) \cdot P(\{X+Y=1\}).

其中，

\begin{gather*} P(\{X=0\}) = P(X=0,Y=0) + P(X=0,Y=1) = 0.4 + a, \\ P(\{X+Y=1\}) = P(X=0,Y=1) + P(X=1,Y=0) = a + b, \\ P(\{X=0\} \cap \{X+Y=1\}) = P(X=0,Y=1) = a. \end{gather*}

代入独立条件得：

a = (0.4 + a)(a + b).

由 $a + b = 0.5$ ，代入得：

a = (0.4 + a) \times 0.5,

解得

a = 0.4,

进而

b = 0.1.

验证：

P(\{X=0\}) = 0.8, \quad P(\{X+Y=1\}) = 0.5, \quad P(\text{交集}) = 0.4,

乘积为 $0.8 \times 0.5 = 0.4$ ，满足独立条件。

因此，选项 B 正确。

14

设 $X_1,X_2, \cdots ,X_n(n \ge 2)$ 为来自总体 $N(0,1)$ 的简单随机样本， $\overline{X}$ 为样本均值， $S^2$ 为样本方差，则

概率论与数理统计数理统计的基本概念

正确答案：D

【解析】

应选 (D)。因 $X_1, X_2, \cdots, X_n(n \geq 2)$ 为来自总体 $N(0,1)$ 的简单随机样本，故有

\overline{X} = \frac{1}{n} \sum_{i=1}^n X_i \sim N(0, \frac{1}{n})

根据正态总体抽样分布理论有

\begin{gather*} \frac{\overline{X}-0}{1/\sqrt{n}} = \sqrt{n}\overline{X} \sim N(0,1), \\ \frac{(n-1)S^2}{\sigma^2} = \frac{(n-1)S^2}{1^2} = (n-1)S^2 \sim \chi^2(n-1), \\ \frac{\overline{X}-0}{S/\sqrt{n}} = \frac{\sqrt{n}\overline{X}}{S} \sim t(n-1); \end{gather*}

故排除选项 (A)、(B)、(C)。又

X_1^2 \sim \chi^2(1), \quad \sum_{i=2}^n X_i^2 \sim \chi^2(n-1),

且 $X_1^2$ 与 $\sum_{i=2}^n X_i^2$ 相互独立，于是

\frac{X_1^2/1}{\sum_{i=2}^n X_i^2/(n-1)} = \frac{(n-1)X_1^2}{\sum_{i=2}^n X_i^2} \sim F(1,n-1).

故应选 (D)。

解答题

15～23小题，共94分

15

（本题满分 11 分）

设 $D = \{(x,y)\left| x^2 + y^2 \le \sqrt{2} ,x \ge 0,y \ge 0 \right.\}$ ， $[1 + x^2 + y^2]$ 表示不超过 $1 + x^2 + y^2$ 的最大整数．计算二重积分 $\iint_D xy[1 + x^2 + y^2]\dx\dy.$

高等数学多元函数积分学重积分的计算

【答案】 $\dfrac{3}{8}$

【解析】 区域 $D$ 是四分之一圆盘 $x^2 + y^2 \le \sqrt{2}$ , $x \ge 0$ , $y \ge 0$ 。引入极坐标变换 $x = r\cos\theta$ , $y = r\sin\theta$ ，则 $D$ 对应于 $0 \le \theta \le \pi/2$ , $0 \le r \le \sqrt{\sqrt{2}} = 2^{1/4}$ 。积分变为：

\iint_D xy[1 + x^2 + y^2] \, dx\,dy = \int_0^{\pi/2} \int_0^{2^{1/4}} r^2 \cos\theta \sin\theta [1 + r^2] \cdot r \, dr\,d\theta = \frac{1}{2} \int_0^{\pi/2} \sin 2\theta \, d\theta \int_0^{2^{1/4}} r^3 [1 + r^2] \, dr.

由于 $1 + r^2 \in [1, 1+\sqrt{2}]$ ，且 $\sqrt{2} \approx 1.414$ ，故 $1 + r^2 \in [1, 2.414)$ ，取整函数 $[1 + r^2]$ 在 $r^2 < 1$ 时取值为 1，在 $r^2 \ge 1$ 时取值为 2。因此将 $r$ 的积分分段：

\int_0^{2^{1/4}} r^3 [1 + r^2] \, dr = \int_0^1 r^3 \cdot 1 \, dr + \int_1^{2^{1/4}} r^3 \cdot 2 \, dr = \left[ \frac{r^4}{4} \right]_0^1 + 2 \left[ \frac{r^4}{4} \right]_1^{2^{1/4}} = \frac{1}{4} + \frac{1}{2} \left( (2^{1/4})^4 - 1 \right) = \frac{1}{4} + \frac{1}{2}(2 - 1) = \frac{3}{4}.

又，

\int_0^{\pi/2} \sin 2\theta \, d\theta = \left[ -\frac{1}{2} \cos 2\theta \right]_0^{\pi/2} = -\frac{1}{2}(-1 - 1) = 1.

因此，

\iint_D xy[1 + x^2 + y^2] \, dx\,dy = \frac{1}{2} \cdot 1 \cdot \frac{3}{4} = \frac{3}{8}.

16

（本题满分 12 分）

求幂级数 $\sum_{n = 1}^{\infty}(- 1)^{n - 1}\left(1 + \frac{1}{n(2n - 1)} \right) x^{2n}$ 的收敛区间与和函数 $f(x)$ ．

高等数学无穷级数求幂级数的收敛半径、收敛区间和收敛域

【答案】
收敛区间为 $(-1, 1)$ ，和函数为

f(x) = \frac{x^2}{1+x^2} - \ln(1 + x^2) + 2x \arctan x.

【解析】
考虑幂级数 $\sum_{n=1}^{\infty} (-1)^{n-1} \left(1 + \frac{1}{n(2n-1)}\right) x^{2n}$ 。令 $y = x^2$ ，则级数化为 $\sum_{n=1}^{\infty} c_n y^n$ ，其中 $c_n = (-1)^{n-1} \left(1 + \frac{1}{n(2n-1)}\right)$ 。
使用比值判别法：

\lim_{n \to \infty} \left| \frac{c_{n+1}}{c_n} \right| = \lim_{n \to \infty} \left| \frac{1 + \frac{1}{(n+1)(2n+1)}}{1 + \frac{1}{n(2n-1)}} \right| = 1,

故收敛半径 $R = 1$ ，即当 $|y| < 1$ 时收敛， $|y| > 1$ 时发散。由于 $y = x^2$ ，有 $|x| < 1$ 时收敛， $|x| > 1$ 时发散。
当 $|x| = 1$ 时，级数为 $\sum_{n=1}^{\infty} (-1)^{n-1} \left(1 + \frac{1}{n(2n-1)}\right)$ 。将其拆分为 $\sum_{n=1}^{\infty} (-1)^{n-1}$ 和 $\sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n(2n-1)}$ 。前者通项不趋于零，发散；后者绝对收敛。故整体在 $|x| = 1$ 时发散。收敛区间为 $(-1, 1)$ 。

求和函数 $f(x)$ ：

f(x) = \sum_{n=1}^{\infty} (-1)^{n-1} \left(1 + \frac{1}{n(2n-1)}\right) x^{2n} = \sum_{n=1}^{\infty} (-1)^{n-1} x^{2n} + \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n(2n-1)} x^{2n} = S_1(x) + S_2(x).

其中

S_1(x) = \sum_{n=1}^{\infty} (-1)^{n-1} x^{2n} = \frac{x^2}{1 + x^2}, \quad |x| < 1.

对于 $S_2(x)$ ：

S_2(x) = \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n(2n-1)} x^{2n}.

分解 $\frac{1}{n(2n-1)} = -\frac{1}{n} + \frac{2}{2n-1}$ ，

S_2(x) = -\sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n} x^{2n} + 2\sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{2n-1} x^{2n} = -A(x) + 2B(x).

其中

A(x) = \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n} x^{2n} = \ln(1 + x^2), \quad |x| < 1,

B(x) = \sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{2n-1} x^{2n} = x^2 \sum_{m=0}^{\infty} (-1)^m \frac{x^{2m}}{2m+1} = x \arctan x, \quad |x| < 1.

故

S_2(x) = -\ln(1 + x^2) + 2x \arctan x.

因此，

f(x) = S_1(x) + S_2(x) = \frac{x^2}{1 + x^2} - \ln(1 + x^2) + 2x \arctan x, \quad |x| < 1.

17

（本题满分 11 分）

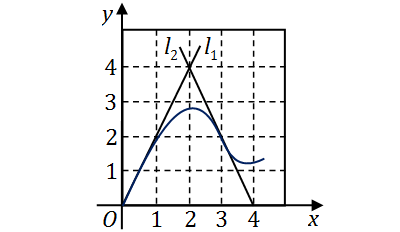
如图，曲线 $C$ 的方程为 $y = f(x)$ ，点 $(3,2)$ 是它的一个拐点，直线 $l_1$ 与 $l_2$ 分别是曲线 $C$ 在点 $(0,0)$ 与 $(3,2)$ 处的切线，其交点为 $(2,4)$ ．设函数 $f(x)$ 具有三阶连续导数，计算定积分 $\int_0^3 (x^2 + x)f'''(x)\dx$ ．

高等数学一元函数积分学变限积分

【答案】 $20$

【解析】

由直线 $l_1$ 过 $(0,0)$ 和 $(2,4)$ 两点知直线 $l_1$ 的斜率为 $2$ 。由直线 $l_1$ 是曲线 $C$ 在点 $(0,0)$ 的切线，由导数的几何意义知 $f'(0) = 2$ 。同理可得 $f'(3) = -2$ 。另外由点 $(3,2)$ 是曲线 $C$ 的一个拐点知 $f''(3) = 0$ 。由分部积分公式，

\begin{align*} \int_{0}^{3} (x^2 + x)f'''(x)dx &= \int_{0}^{3} (x^2 + x)d(f''(x)) \\ &= [(x^2 + x)f''(x)]_{0}^{3} - \int_{0}^{3} f''(x)(2x+1)dx \\ &= -\int_{0}^{3} (2x+1)d(f'(x)) \\ &= -[(2x+1)f'(x)]_{0}^{3} + 2\int_{0}^{3} f'(x)dx \\ &= 16 + 2[f(3) - f(0)] = 20. \end{align*}

18

（本题满分 12 分）

已知函数 $f(x)$ 在 $[0,1]$ 上连续，在 $(0,1)$ 内可导，且 $f(0) = 0,f(1) = 1$ ．证明：

(1) 存在 $\xi \in(0,1),$ 使得 $f(\xi) = 1 - \xi$ ；

(2) 存在两个不同的点 $\eta ,\zeta \in(0,1)$ ，使得 $f'(\eta)f'(\zeta) = 1$ ．

高等数学一元函数微分学微分中值定理

【解析】
(1) 令 $g(x) = f(x) + x - 1$ 。由于 $f(x)$ 在 $[0,1]$ 上连续，故 $g(x)$ 在 $[0,1]$ 上连续。计算得 $g(0) = f(0) + 0 - 1 = -1 < 0$ ， $g(1) = f(1) + 1 - 1 = 1 > 0$ 。由介值定理，存在 $\xi \in (0,1)$ 使得 $g(\xi) = 0$ ，即 $f(\xi) + \xi - 1 = 0$ ，所以 $f(\xi) = 1 - \xi$ 。

(2) 由 (1) 知存在 $\xi \in (0,1)$ 满足 $f(\xi) = 1 - \xi$ 。在区间 $[0,\xi]$ 上应用拉格朗日中值定理，存在 $\eta \in (0,\xi)$ 使得

f'(\eta) = \frac{f(\xi) - f(0)}{\xi - 0} = \frac{1 - \xi}{\xi}.

在区间 $[\xi,1]$ 上应用拉格朗日中值定理，存在 $\zeta \in (\xi,1)$ 使得

f'(\zeta) = \frac{f(1) - f(\xi)}{1 - \xi} = \frac{1 - (1 - \xi)}{1 - \xi} = \frac{\xi}{1 - \xi}.

于是，

f'(\eta) f'(\zeta) = \frac{1 - \xi}{\xi} \cdot \frac{\xi}{1 - \xi} = 1.

由于 $\eta \in (0,\xi)$ 和 $\zeta \in (\xi,1)$ ，故 $\eta$ 和 $\zeta$ 是两个不同的点。

19

（本题满分 12 分）

设函数 $\phi (y)$ 具有连续导数，在围绕原点的任意分段光滑简单闭曲线 $L$ 上，曲线积分 $\oint_L \frac{\phi(y)\dx + 2xy\dy}{2x^2 + y^4}$ 的值恒为同一常数．

(1) 证明：对右半平面 $x > 0$ 内的任意分段光滑简单闭曲线 $C$ ，有

\oint_C \frac{\phi(y)\dx + 2xy\dy}{2x^2 + y^4} = 0.

(2) 求函数 $\phi (y)$ 的表达式．

高等数学多元函数积分学第二类曲线积分

【答案】
(1) 对于右半平面 $x > 0$ 内的任意分段光滑简单闭曲线 $C$ ，有 $\oint_C \frac{\phi(y)\dx + 2xy\dy}{2x^2 + y^4} = 0$ 。
(2) $\phi(y) = -y^2$ 。

【解析】
(1) 由于在围绕原点的任意分段光滑简单闭曲线 $L$ 上，曲线积分 $\oint_L \frac{\phi(y)\dx + 2xy\dy}{2x^2 + y^4}$ 的值恒为同一常数，考虑右半平面 $x > 0$ 内的任意分段光滑简单闭曲线 $C$ 。因为 $C$ 不包含原点，且被积函数在 $x > 0$ 内具有连续偏导数（分母 $2x^2 + y^4 > 0$ ），所以 $C$ 可以在 $x > 0$ 内连续收缩为一点。在收缩过程中，曲线积分值保持不变，当收缩为一点时，曲线积分为零，因此沿 $C$ 的曲线积分为零。

(2) 由条件知，曲线积分在围绕原点的闭曲线上为常数，这意味着被积函数在原点外满足 $\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$ ，其中 $P = \frac{\phi(y)}{2x^2 + y^4}$ ， $Q = \frac{2xy}{2x^2 + y^4}$ 。
计算偏导数：

\frac{\partial Q}{\partial x} = \frac{\partial}{\partial x} \left( \frac{2xy}{2x^2 + y^4} \right) = \frac{2y(2x^2 + y^4) - 2xy \cdot 4x}{(2x^2 + y^4)^2} = \frac{4x^2 y + 2y^5 - 8x^2 y}{(2x^2 + y^4)^2} = \frac{2y^5 - 4x^2 y}{(2x^2 + y^4)^2},

\frac{\partial P}{\partial y} = \frac{\partial}{\partial y} \left( \frac{\phi(y)}{2x^2 + y^4} \right) = \frac{\phi'(y)(2x^2 + y^4) - \phi(y) \cdot 4y^3}{(2x^2 + y^4)^2}.

令两者相等：

\frac{\phi'(y)(2x^2 + y^4) - 4y^3 \phi(y)}{(2x^2 + y^4)^2} = \frac{2y^5 - 4x^2 y}{(2x^2 + y^4)^2},

即

\phi'(y)(2x^2 + y^4) - 4y^3 \phi(y) = 2y^5 - 4x^2 y.

整理得：

2x^2 \phi'(y) + \phi'(y) y^4 - 4y^3 \phi(y) = -4x^2 y + 2y^5.

比较 $x^2$ 的系数：

2 \phi'(y) = -4y \quad \Rightarrow \quad \phi'(y) = -2y.

代入上式：

(-2y) \cdot y^4 - 4y^3 \phi(y) = 2y^5 \quad \Rightarrow \quad -2y^5 - 4y^3 \phi(y) = 2y^5 \quad \Rightarrow \quad -4y^3 \phi(y) = 4y^5 \quad \Rightarrow \quad \phi(y) = -y^2.

因此，函数 $\phi(y) = -y^2$ 。

20

（本题满分 9 分）

已知二次型 $f(x_1,x_2,x_3) = (1 - a)x_1^2 + (1 - a)x_2^2 + 2x_3^2 + 2(1 + a) x_1x_2$ 的秩为 $2$ ．

(1) 求 $a$ 的值；

(2) 求正交变换 $x = Qy$ ，把 $f(x_1,x_2,x_3)$ 化成标准形；

(3) 求方程 $f(x_1,x_2,x_3)=0$ 的解．

线性代数二次型

【答案】

(1) $a = 0$
(2) 正交变换 $x = Qy$ 中， $Q = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{pmatrix}$ ，标准形为 $f = 2y_2^2 + 2y_3^2$
(3) 方程 $f(x_1, x_2, x_3) = 0$ 的解为 $x_1 = t, x_2 = -t, x_3 = 0$ ，其中 $t$ 为任意实数。

【解析】 (1) 二次型 $f(x_1, x_2, x_3)$ 的矩阵为 $A = \begin{pmatrix} 1 - a & 1 + a & 0 \\ 1 + a & 1 - a & 0 \\ 0 & 0 & 2 \end{pmatrix}$ 。秩为 2 意味着 $\det(A) = 0$ 。计算行列式：

\det(A) = \det \begin{pmatrix} 1 - a & 1 + a \\ 1 + a & 1 - a \end{pmatrix} \times 2 = [(1 - a)^2 - (1 + a)^2] \times 2 = [-4a] \times 2 = -8a

设 $-8a = 0$ ，得 $a = 0$ 。当 $a = 0$ 时，矩阵 $A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}$ ，秩为 2，符合条件。

(2) 当 $a = 0$ 时，二次型为 $f(x_1, x_2, x_3) = x_1^2 + x_2^2 + 2x_3^2 + 2x_1 x_2$ ，矩阵 $A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}$ 。求特征值和特征向量：
特征多项式为 $\det(A - \lambda I) = \det \begin{pmatrix} 1 - \lambda & 1 & 0 \\ 1 & 1 - \lambda & 0 \\ 0 & 0 & 2 - \lambda \end{pmatrix} = (\lambda^2 - 2\lambda)(2 - \lambda) = -\lambda(\lambda - 2)^2$ ，特征值为 $\lambda = 0$ （单根）和 $\lambda = 2$ （二重根）。
对于 $\lambda = 0$ ，解 $(A - 0I)v = 0$ 得特征向量 $(1, -1, 0)^T$ ，单位化得 $u_1 = \left( \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}, 0 \right)^T$ 。
对于 $\lambda = 2$ ，解 $(A - 2I)v = 0$ 得特征向量 $(1, 1, 0)^T$ 和 $(0, 0, 1)^T$ ，单位化得 $u_2 = \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0 \right)^T$ 和 $u_3 = (0, 0, 1)^T$ 。
正交矩阵 $Q = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{pmatrix}$ ，标准形为 $f = 0 \cdot y_1^2 + 2 \cdot y_2^2 + 2 \cdot y_3^2 = 2y_2^2 + 2y_3^2$ 。

(3) 由标准形 $f = 2y_2^2 + 2y_3^2 = 0$ 得 $y_2 = 0$ ， $y_3 = 0$ ， $y_1$ 任意。代入正交变换 $x = Qy$ ：

x = Q \begin{pmatrix} y_1 \\ 0 \\ 0 \end{pmatrix} = y_1 \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ 0 \end{pmatrix}

令 $t = \frac{y_1}{\sqrt{2}}$ ，则解为 $x_1 = t$ ， $x_2 = -t$ ， $x_3 = 0$ ，其中 $t$ 为任意实数。

21

（本题满分 9 分）

已知 $3$ 阶矩阵 $A$ 的第一行是 $(a,b,c)$ ， $a,b,c$ 不全为零，矩阵 $B = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & k \end{pmatrix}$ （ $k$ 为常数），且 $AB = 0$ ，求线性方程组 $Ax = 0$ 的通解．

线性代数线性方程组

【解析】

由 $AB = 0$ 知， $B$ 的每一列均为 $Ax = 0$ 的解，且 $r(A) + r(B) \leq 3$ 。

(Ⅰ) 若 $k \neq 9$ ，则 $r(B) = 2$ ，于是 $r(A) = 1$ 。记 $B = (\beta_1, \beta_2, \beta_3)$ ，则 $\beta_1, \beta_3$ 是方程组的解且线性无关，可作为其基础解系，故 $Ax = 0$ 的通解为：

x = k_1 \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + k_2 \begin{pmatrix} 3 \\ 6 \\ k \end{pmatrix}, \quad k_1, k_2 \text{为任意常数。}

(Ⅱ) 若 $k = 9$ ，则 $r(B) = 1$ ，于是 $r(A) = 1$ 或 $r(A) = 2$ 。

(i) 若 $r(A) = 2$ ，则方程组的基础解系由一个线性无关的解组成， $\beta_1$ 是方程组 $Ax = 0$ 的基础解系，则 $Ax = 0$ 的通解为：

x = k_1 \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \quad k_1 \text{为任意常数。}

(ii) 若 $r(A) = 1$ ，则 $A$ 的三个行向量成比例，因第 1 行元素 $(a, b, c)$ 不全为零，不妨设 $a \neq 0$ ，则 $Ax = 0$ 的同解方程组为： $ax_1 + bx_2 + cx_3 = 0$ ，系数矩阵的秩为 1，故基础解系由 2 个线性无关解向量组成，选 $x_2, x_3$ 为自由未知量，分别取 $x_2 = 1, x_3 = 0$ 或 $x_2 = 0, x_3 = 1$ ，方程组的基础解系为

\xi_1 = \begin{pmatrix} -\frac{b}{a} \\ 1 \\ 0 \end{pmatrix}, \quad \xi_2 = \begin{pmatrix} -\frac{c}{a} \\ 0 \\ 1 \end{pmatrix},

则其通解为 $x = k_1 \xi_1 + k_2 \xi_2$ ， $k_1, k_2$ 为任意常数。

22

（本题满分 9 分）

设二维随机变量 $(X,Y)$ 的概率密度为 $f(x,y) = \begin{cases} 1, & 0 < x < 1,0 < y < 2x, \\ 0, & \text{其他}. \end{cases}$ 求：

(1) $(X,Y)$ 的边缘概率密度 $f_X(x),f_Y(y)$ ；

(2) $Z = 2X - Y$ 的概率密度 $f_Z(z)$ ．

概率论与数理统计多维随机变量及其分布边缘分布和条件分布

【答案】
(1) $f_X(x) = \begin{cases} 2x, & 0 < x < 1, \\ 0, & \text{其他} \end{cases}$
$f_Y(y) = \begin{cases} 1 - \frac{y}{2}, & 0 < y < 2, \\ 0, & \text{其他} \end{cases}$

(2) $f_Z(z) = \begin{cases} 1 - \frac{z}{2}, & 0 < z < 2, \\ 0, & \text{其他} \end{cases}$

【解析】

(1) 边缘概率密度计算

对于 $f_X(x)$ ，通过对 $y$ 积分得到
$f_X(x) = \int_{-\infty}^{\infty} f(x,y) \, dy.$
当 $0 < x < 1$ 时， $y$ 的范围为 $0 < y < 2x$ ，于是
$f_X(x) = \int_{0}^{2x} 1 \, dy = 2x.$
其他情况下， $f_X(x) = 0$ 。
对于 $f_Y(y)$ ，通过对 $x$ 积分得到
$f_Y(y) = \int_{-\infty}^{\infty} f(x,y) \, dx.$
当 $0 < y < 2$ 时， $x$ 的范围为 $\frac{y}{2} < x < 1$ ，因此
$f_Y(y) = \int_{y/2}^{1} 1 \, dx = 1 - \frac{y}{2}.$
其他情况下， $f_Y(y) = 0$ 。

(2) $Z = 2X - Y$ 的概率密度计算

采用累积分布函数（CDF）方法。首先计算

F_Z(z) = P(Z \leq z) = P(2X - Y \leq z).

由于 $f(x,y)$ 在区域 $0 < x < 1, \; 0 < y < 2x$ 上为 1，其余为 0，可得：

当 $z < 0$ 时， $F_Z(z) = 0$ ；
当 $z > 2$ 时， $F_Z(z) = 1$ 。

对于 $0 < z < 2$ ，计算概率 $P(2X - Y \leq z)$ 在区域

0 < x < 1, \quad 0 < y < 2x, \quad y \geq 2x - z

上的积分。将 $x$ 分为两个区间：

当 $x \in [0, z/2]$
此时 $y$ 从 $0$ 到 $2x$ ，积分值为
$\int_{0}^{z/2} \int_{0}^{2x} 1 \, dy \, dx = \int_{0}^{z/2} 2x \, dx = \frac{z^2}{4}.$
当 $x \in [z/2, 1]$
此时 $y$ 从 $2x - z$ 到 $2x$ ，积分值为
$\int_{z/2}^{1} \int_{2x - z}^{2x} 1 \, dy \, dx = \int_{z/2}^{1} z \, dx = z\left(1 - \frac{z}{2}\right) = z - \frac{z^2}{2}.$

因此，

F_Z(z) = \frac{z^2}{4} + \left(z - \frac{z^2}{2}\right) = z - \frac{z^2}{4}.

对 $F_Z(z)$ 求导，得到

f_Z(z) = \frac{d}{dz} \left(z - \frac{z^2}{4}\right) = 1 - \frac{z}{2}, \quad 0 < z < 2,

其他情况下 $f_Z(z) = 0$ 。

验证：

\int_{0}^{2} \left(1 - \frac{z}{2}\right) dz = 1,

满足概率密度函数的性质。

23

（本题满分 9 分）

设 $X_1,X_2, \cdots ,X_n(n > 2)$ 为来自总体 $N(0,1)$ 的简单随机样本， $\overline{X}$ 为样本均值，记 $Y_i = X_i - \overline{X}$ ， $i = 1,2, \cdots ,n$ ．求：

(1) $Y_i$ 的方差 $DY_i$ ， $i = 1,2, \cdots ,n$ ；

(2) $Y_1$ 与 $Y_n$ 的协方差 $\Cov (Y_1,Y_n)$ ．

概率论与数理统计随机变量的数字特征协方差与相关系数

【答案】
(1) $DY_i = 1 - \frac{1}{n}$
(2) $\Cov(Y_1, Y_n) = -\frac{1}{n}$

【解析】
(1) 由于 $X_1, X_2, \cdots, X_n$ 独立同分布于 $N(0,1)$ ，有 $EX_i = 0$ ， $DX_i = 1$ 。样本均值 $\overline{X} = \frac{1}{n} \sum_{i=1}^n X_i$ ，则 $E\overline{X} = 0$ ， $D\overline{X} = \frac{1}{n}$ 。
计算 $Y_i = X_i - \overline{X}$ 的方差：

DY_i = D(X_i - \overline{X}) = DX_i + D\overline{X} - 2\Cov(X_i, \overline{X})

其中 $\Cov(X_i, \overline{X}) = \Cov\left(X_i, \frac{1}{n} \sum_{j=1}^n X_j\right) = \frac{1}{n} \sum_{j=1}^n \Cov(X_i, X_j)$ 。
由于 $X_i$ 独立，当 $i = j$ 时 $\Cov(X_i, X_j) = DX_i = 1$ ，当 $i \neq j$ 时 $\Cov(X_i, X_j) = 0$ ，故 $\Cov(X_i, \overline{X}) = \frac{1}{n}$ 。
代入得：

DY_i = 1 + \frac{1}{n} - 2 \cdot \frac{1}{n} = 1 - \frac{1}{n}

因此， $DY_i = 1 - \frac{1}{n}$ 。

(2) 计算 $Y_1$ 与 $Y_n$ 的协方差：

Y_1 = X_1 - \overline{X}, \quad Y_n = X_n - \overline{X}

\Cov(Y_1, Y_n) = \Cov(X_1 - \overline{X}, X_n - \overline{X}) = \Cov(X_1, X_n) - \Cov(X_1, \overline{X}) - \Cov(\overline{X}, X_n) + \Cov(\overline{X}, \overline{X})

由于 $X_1$ 与 $X_n$ 独立， $\Cov(X_1, X_n) = 0$ 。
已知 $\Cov(X_1, \overline{X}) = \frac{1}{n}$ ， $\Cov(\overline{X}, X_n) = \frac{1}{n}$ ， $\Cov(\overline{X}, \overline{X}) = D\overline{X} = \frac{1}{n}$ 。
代入得：

\Cov(Y_1, Y_n) = 0 - \frac{1}{n} - \frac{1}{n} + \frac{1}{n} = -\frac{1}{n}

因此， $\Cov(Y_1, Y_n) = -\frac{1}{n}$ 。