卷 3
填空题
1~6小题,每小题4分,共24分
1
极限
limx→∞xsinx2+12x=
______.
【答案】
2
【解析】
考虑极限
limx→∞xsinx2+12x
。
当
x→∞
时,
x2+12x→0
,因此可利用等价无穷小替换
sinu∼u
(当
u→0
),即
sinx2+12x∼x2+12x
。
于是原极限化为
x→∞limx⋅x2+12x=x→∞limx2+12x2.
分子分母同除以
x2
,得
x→∞lim1+x212=1+02=2.
因此,极限值为
2
。
2
微分方程
xy′+y=0
满足初始条件
y(1)=2
的特解为 ______.
【答案】
y=x2
【解析】
给定微分方程
xy′+y=0
,可以写为
xdxdy+y=0
。
通过分离变量法,将方程整理为
ydy=−xdx
。
两边积分得
ln∣y∣=−ln∣x∣+C
,其中
C
为积分常数。
简化得
ln∣y∣=lnx1+C
,即
∣y∣=eCx1
。
令
K=eC
,则通解为
y=xK
。
代入初始条件
y(1)=2
,得
2=1K
,因此
K=2
。
故特解为
y=x2
。
3
设二元函数
z=xex+y+(x+1)ln(1+y)
,则
dz(1,0)=
______.
【答案】
2edx+(e+2)dy
【解析】
求偏导数得
∂x∂z=ex+y+xex+y+ln(1+y),∂y∂z=xex+y+1+yx+1.
于是
z
的全微分为
dz=∂x∂zdx+∂y∂zdy=(ex+y+xex+y+ln(1+y))dx+(xex+y+y+1x+1)dy.
所以
dz∣(1,0)=2edx+(e+2)dy
。
4
设行向量组
(2,1,1,1)
,
(2,1,a,a)
,
(3,2,1,a)
,
(4,3,2,1)
线性相关,且
a=1
,则
a=
______.
【答案】
21
【解析】
给定行向量组:
α1=(2,1,1,1),α2=(2,1,a,a),α3=(3,2,1,a),α4=(4,3,2,1)
线性相关,且
a=1
。由于向量个数等于维数,线性相关等价于由这些向量作为行构成的矩阵的行列式为零。
构造矩阵:
计算行列式
det(A)
。
首先进行行变换:
- R2←R2−R1
,得:
203410231a−1121a−1a1
由于
a=1
,可从第二行提取公因子
a−1
:
det(A)=(a−1)⋅det20341023111211a1
记上述矩阵为
A′
,计算
det(A′)
。
继续行变换:
- R3←R3−R1
,得:
20141013110211a−11
- R4←R4−2R1
,得:
20101011110011a−1−1
按第三列展开行列式。第三列元素为:
- a13=1
,余子式
C13
;
- a23=1
,余子式
C23
;
- a33=0
,
a43=0
。
计算
C13
(删除第一行、第三列):
C13=det0100111a−1−1=1⋅det(1011)=1⋅(1⋅1−1⋅0)=1 计算
C23
(删除第二行、第三列):
C23=(−1)2+3⋅det2101111a−1−1=−1⋅[2⋅(1⋅(−1)−(a−1)⋅1)−1⋅(1⋅(−1)−(a−1)⋅0)+1⋅(1⋅1−1⋅0)]=−1⋅[2(−1−(a−1))−1(−1)+1(1)]=−1⋅[2(−a)+1+1]=−1⋅(−2a+2)=2a−2 所以:
det(A′)=1⋅C13+1⋅C23=1+(2a−2)=2a−1
于是:
det(A)=(a−1)(2a−1)
令
det(A)=0
,得
(a−1)(2a−1)=0
。由
a=1
,得
a=21
。
因此,答案为
21
。
5
同试卷 1 第 6 题
6
设二维随机变量
(X,Y)
的概率分布为
X∖Y0100.4b1a0.1
已知随机事件
{X=0}
与
{X+Y=1}
相互独立,则
a=
______,
b=
______.
【答案】
0.4,0.1
【解析】
由概率分布的性质,所有概率之和为1,即:
0.4+a+b+0.1=1
解得:
a+b=0.5
事件
{X=0}
的概率为:
P(X=0)=P(X=0,Y=0)+P(X=0,Y=1)=0.4+a
事件
{X+Y=1}
的概率为:
P(X+Y=1)=P(X=0,Y=1)+P(X=1,Y=0)=a+b
事件
{X=0}
与
{X+Y=1}
的交集为
{X=0,Y=1}
,其概率为
a
。由独立性条件:
P({X=0}∩{X+Y=1})=P(X=0)⋅P(X+Y=1)
即:
a=(0.4+a)(a+b)
代入
a+b=0.5
:
a=(0.4+a)×0.5
解得:
a=0.2+0.5a
a=0.4
代入
a+b=0.5
:
b=0.1
验证:
P(X=0)=0.4+0.4=0.8
,
P(X+Y=1)=0.4+0.1=0.5
,
P({X=0}∩{X+Y=1})=0.4
,且
0.8×0.5=0.4
,满足独立性条件。
选择题
7~14小题,每小题4分,共32分
7
当
a
取下列哪个值时,函数
f(x)=2x3−9x2+12x−a
恰好有两个不同的零点
正确答案:B【解析】 因为
f′(x)=6x2−18x+12=6(x−1)(x−2)
,知可能极值点为
x=1
和
x=2
。从而可将函数划分为 3 个严格单调区间:
xf′(x)(−∞,1)+(1,2)−(2,+∞)+
并且
limx→−∞f(x)=−∞
,
limx→+∞f(x)=+∞
。若
f(x)
恰好有两个零点,则必有
f(1)=0
或
f(2)=0
(否则有一个或三个零点),解之得
a=5
或
a=4
。故选 (B)。
8
设
I1=∬Dcosx2+y2dσ
,
I2=∬Dcos(x2+y2)dσ
,
I3=∬Dcos(x2+y2)2dσ
,其中
D={(x,y)x2+y2≤1}
,则
正确答案:A【解析】 在区域
D={(x,y)∣x2+y2≤1}
上,除原点
x2+y2=0
及边界
x2+y2=1
外,总有
而在
0≤u≤1
内,
cosu
是严格单调减函数,于是
cos(x2+y2)2>cos(x2+y2)>cosx2+y2. 因此二重积分
∬Dcos(x2+y2)2dσ>∬Dcos(x2+y2)dσ>∬Dcosx2+y2dσ, 即
I3>I2>I1
.
9
设
an>0
,
n=1,2,⋯
,若
∑n=1∞an
发散,
∑n=1∞(−1)n−1an
收敛,则下列结论正确的是
正确答案:D【解析】 给定
an>0
,
∑n=1∞an
发散,但
∑n=1∞(−1)n−1an
收敛。由交错级数收敛可知
an→0
。
考虑选项 D:
∑n=1∞(a2n−1−a2n)
。交错级数的部分和
S2N=n=1∑N(a2n−1−a2n),
由于交错级数收敛,
S2N
收敛,因此
∑n=1∞(a2n−1−a2n)
收敛。
选项 A 和 B 不一定成立,例如取
an=n1
时,
∑a2n−1
和
∑a2n
均发散。
选项 C 中
∑(a2n−1+a2n)=∑an
,发散。
故 D 正确。
10
设
f(x)=xsinx+cosx
,下列命题中正确的是
正确答案:B【解析】 首先,求函数
f(x)=xsinx+cosx
的导数:
f′(x)=dxd(xsinx)+dxd(cosx)=sinx+xcosx−sinx=xcosx
令
f′(x)=0
,得
xcosx=0
,解得临界点
x=0
或
x=2π+kπ
(
k
为整数)。本题关注
x=0
和
x=2π
。
为判断极值类型,求二阶导数:
f′′(x)=dxd(xcosx)=cosx−xsinx
在
x=0
处,
f′′(0)=cos0−0⋅sin0=1>0
故
x=0
为极小值点。
在
x=2π
处,
f′′(2π)=cos2π−2πsin2π=0−2π⋅1=−2π<0
故
x=2π
为极大值点。
因此,
f(0)
是极小值,
f(2π)
是极大值,对应选项 B。
11
以下四个命题中,正确的是
正确答案:C【解析】 设
f(x)=x1
,则
f(x)
及
f′(x)=−x21
均在
(0,1)
内连续,但
f(x)
在
(0,1)
内无界,故排除 (A) 和 (B)。又
f(x)=x
在
(0,1)
内有界,但
f′(x)=2x1
在
(0,1)
内无界,故排除 (D)。
如果
f′(x)
在区间
(0,1)
内有界,则对于正数
M
,使
(0,1)
内的一切
x
,有
∣f′(x)∣≤M
。在
(0,1)
内取定点
x0
,则对于任意
x∈(0,1)
有
f(x)−f(x0)=f′(ξ)(x−x0),ξ∈(0,1).
于是
∣f(x)∣≤∣f(x0)∣+∣f′(ξ)∣∣x−x0∣≤∣f(x0)∣+M,
所以
f(x)
在
(0,1)
内有界。
12
设矩阵
A
=
(aij)3×3
满足
A∗=AT
,其中
A∗
是
A
的伴随矩阵,
AT
为
A
的转置矩阵.
若
a11,a12,a13
为三个相等的正数,则
a11
为
正确答案:A【解析】 由已知条件
A∗=A11A12A13A21A22A23A31A32A33=a11a12a13a21a22a23a31a32a33=AT, 则有
aij=Aij
,
i,j=1,2,3
,其中
Aij
为
aij
的代数余子式。又由
A∗=AT
和
AA∗=∣A∣E
得
AAT=∣A∣E
,两边取行列式,得到
∣A∣2=∣A∣3
,于是有
∣A∣=0
或
∣A∣=1
。而
∣A∣=a11A11+a12A12+a13A13=a112+a122+a132=3a112=0,
于是
∣A∣=1
,即
3a112=1
,故
a11=33
。故正确选项为 (A)。
13
同试卷 1 第 11 题
14
设一批零件的长度服从正态分布
N(μ,σ2)
,其中
μ,σ2
均未知.
现从中随机抽取
16
个零件,测得样本均值
x=20(cm)
,样本标准差
s=1(cm)
,
则
μ
的置信度为
0.90
的置信区间是
正确答案:C【解析】 由于总体方差未知,样本量较小(
n=16
),需使用
t
分布构建置信区间。置信度为
0.90
,则显著性水平
α=0.10
,
α/2=0.05
。自由度为
n−1=15
。置信区间公式为:
代入数据得:
20±t0.05(15)⋅161=20±41t0.05(15) 因此,置信区间为
(20−41t0.05(15),20+41t0.05(15))
对应选项 C。选项 A 和 B 自由度错误,选项 D 分位数错误。
解答题
本题共9小题,满分94分
15
(本题满分 8 分)
x→0lim(1−e−x1+x−x1)=
【答案】
23
【解析】
考虑极限
limx→0(1−e−x1+x−x1)
。直接代入
x=0
会得到未定式,因此采用洛必达法则或泰勒展开求解。
方法一:泰勒展开
首先,将
e−x
展开为泰勒级数:
e−x=1−x+2!x2−3!x3+O(x4)
,则
1−e−x=x−2x2+6x3−O(x4)
。
于是,
1−e−x1+x=x−2x2+6x3−O(x4)1+x=(x1+1)⋅1−2x+6x2−O(x3)1.
令
g(x)=1−2x+6x2−O(x3)1
,其泰勒展开为:
g(x)=1+2x+12x2+O(x3).
因此,
1−e−x1+x=(x1+1)(1+2x+12x2+O(x3))=x1+23+127x+O(x2).
原表达式为:
(x1+23+127x+O(x2))−x1=23+127x+O(x2).
当
x→0
时,极限为
23
.
方法二:洛必达法则
将表达式通分:
x→0limx(1−e−x)x(1+x)−(1−e−x)=x→0limx(1−e−x)e−x+x+x2−1.
当
x→0
时,分子和分母均趋于 0,应用洛必达法则。
分子导数:
−e−x+1+2x
,分母导数:
1−e−x+xe−x
。
在
x=0
处,分子导数为 0,分母导数为 0,仍需洛必达法则。
二阶分子导数:
e−x+2
,二阶分母导数:
2e−x−xe−x
。
在
x=0
处,二阶分子导数为 3,二阶分母导数为 2,因此极限为
23
。
两种方法均得极限为
23
.
16
(本题满分 8 分)
设
f(u)
具有二阶连续导数,且
g(x,y)=f(xy)+yf(yx)
,
求
x2∂x2∂2g−y2∂y2∂2g
.
【答案】
x2yf′(xy)
【解析】
设
g(x,y)=f(xy)+yf(yx)
,其中
f(u)
具有二阶连续导数。
首先,求一阶偏导数:
∂x∂g=−x2yf′(xy)+f′(yx)
∂y∂g=x1f′(xy)+f(yx)−yxf′(yx)
然后,求二阶偏导数:
∂x2∂2g=x32yf′(xy)+x4y2f′′(xy)+y1f′′(yx)
所以,
x2∂x2∂2g=x2yf′(xy)+x2y2f′′(xy)+yx2f′′(yx)
∂y2∂2g=x21f′′(xy)+y3x2f′′(yx)
所以,
y2∂y2∂2g=x2y2f′′(xy)+yx2f′′(yx)
因此,
x2∂x2∂2g−y2∂y2∂2g=(x2yf′(xy)+x2y2f′′(xy)+yx2f′′(yx))−(x2y2f′′(xy)+yx2f′′(yx))=x2yf′(xy)
故结果为
x2yf′(xy)
.
17
(本题满分 9 分)
同试卷 2 第 21 题
18
(本题满分 9 分)
求幂级数
∑n=1∞(2n+11−1)x2n
在区间
(−1,1)
内的和函数
S(x)
.
【答案】
S(x)=⎩⎨⎧−1+2x1ln1−x1+x−1−x21,0,∣x∣<1,x=0;x=0. 【解析】
将幂级数分为两部分:
S(x)=n=1∑∞(2n+11−1)x2n=n=1∑∞2n+11x2n−n=1∑∞x2n=S1(x)−S2(x).
先求级数
S2(x)
:
S2(x)=n=1∑∞x2n=x2n=0∑∞xn=1−x2x2.
再求级数
S1(x)
:由于
(xS1(x))′=(n=1∑∞2n+1x2n+1)′=n=1∑∞(2n+1x2n+1)′=n=1∑∞x2n=1−x2x2,
因此由微积分基本公式得
xS1(x)=0×S1(0)+∫0x1−t2t2dt=−x+21ln1−x1+x.
又由于
S1(0)=0
,故
S1(x)=⎩⎨⎧−1+2x1ln1−x1+x,0,∣x∣<1,x=0. 所以原幂级数的和函数
S(x)=S1(x)−S2(x)=⎩⎨⎧−1+2x1ln1−x1+x−1−x21,0,∣x∣<1,x=0;x=0. 19
(本题满分 8 分)
设
f(x),g(x)
在
[0,1]
上的导数连续,且
f(0)=0
,
f′(x)≥0
,
g′(x)≥0
.
证明:对任何
a∈[0,1]
,有
∫0ag(x)f′(x)dx+∫01f(x)g′(x)dx≥f(a)g(1).
【答案】 证明见解析。
【解析】
将
a
看成变限,设
F(x)=∫0xg(t)f′(t)dt+∫01f(t)g′(t)dt−f(x)g(1),
则
F(x)
在
[0,1]
上的导数连续,并且
F′(x)=g(x)f′(x)−f′(x)g(1)=f′(x)[g(x)−g(1)].
由
x∈[0,1]
时,
g′(x)≥0
知
g(x)
是单调递增的,所以
g(x)−g(1)≤0
;又
f′(x)≥0
,因此
F′(x)≤0
,即
F(x)
在
[0,1]
上单调递减。另一方面,
F(1)=∫01g(t)f′(t)dt+∫01f(t)g′(t)dt−f(1)g(1).
由分部积分公式
∫01g(t)f′(t)dt=∫01g(t)d[f(t)]=[g(t)f(t)]01−∫01f(t)g′(t)dt=f(1)g(1)−∫01f(t)g′(t)dt,
故
F(1)=0
。因此当
x∈[0,1]
时
F(x)≥F(1)=0
。由此对任何
a∈[0,1]
有
∫0ag(x)f′(x)dx+∫01f(x)g′(x)dx≥f(a)g(1).
20
(本题满分 13 分)
已知齐次线性方程组
(I)
⎩⎨⎧x1+2x2+3x3=0,2x1+3x2+5x3=0,x1+x2+ax3=0,
和(II)
{x1+bx2+cx3=0,2x1+b2x2+(c+1)x3=0,
同解,求
a,b,c
的值.
【答案】
a=2
,
b=1
,
c=2
【解析】
首先,考虑齐次线性方程组(I)的系数矩阵:
对其进行行化简:
当
a=2
时,秩为3,方程组(I)只有零解。但方程组(II)有两个方程、三个变量,不可能只有零解(系数矩阵秩最大为2),故
a=2
不成立。因此
a=2
。
当
a=2
时,方程组(I)的系数矩阵行化简为:
解为:
x1=−x3,x2=−x3
即解空间由向量
v=(−1,−1,1)
张成。
由于方程组(I)和(II)同解,
v
必须满足方程组(II):
{−1+b(−1)+c(1)=02(−1)+b2(−1)+(c+1)(1)=0
化简得:
{c−b=1c−b2=1
相减得
b2−b=0
,即
b(b−1)=0
,解得
b=0
或
b=1
。
若
b=0
,则
c=1
。方程组(II)为:
{x1+x3=02x1+2x3=0
方程相互依赖,解空间维数为2(
x1=−x3
,
x2
自由),与方程组(I)解空间维数1不同,故不成立。
若
b=1
,则
c=2
。方程组(II)为:
{x1+x2+2x3=02x1+x2+3x3=0
系数矩阵为:
(121123)
行化简后秩为2,解空间维数为1,解为
x1=−x3
,
x2=−x3
,即与方程组(I)解空间相同。
因此,
a=2
,
b=1
,
c=2
。
21
(本题满分 13 分)
设
D=(ACTCB)
为正定矩阵,其中
A,B
分别为
m
阶,
n
阶对称矩阵,
C
为
m×n
矩阵.
(1) 计算
PTDP
,其中
P=(EmO−A−1CEn)
;
(2) 利用(I)的结果判断矩阵
B−CTA−1C
是否为正定矩阵,并证明你的结论.
【答案】
(1)
PTDP=(AOOB−CTA−1C)
(2) 矩阵
B−CTA−1C
是正定矩阵。
【解析】
(I) 因为
P=(EmO−A−1CEn)
,所以
PT=(Em−CT(A−1)TOEn)
。
因为
A
为对称矩阵,故
AT=A
,左右两边取逆,
(AT)−1=A−1
。
根据可逆矩阵的性质,又有
(AT)−1=(A−1)T
,故
(A−1)T=A−1
,
所以
PT=(Em−CTA−1OEn)
因此,
PTDP=(Em−CTA−1OEn)(ACTCB)(EmO−A−1CEn)
=(AOCB−CTA−1C)(EmO−A−1CEn)=(AOOB−CTA−1C).
(II) 矩阵
B−CTA−1C
是正定矩阵。事实上,因为
P
可逆,所以由
D
是正定矩阵知
PTDP
也是正定的。
根据正定的定义,对任意的
(OY)=O
,恒有
(O,YT)PTDP(OY)=(O,YT)(AOOB−CTA−1C)(OY)>0.
计算分块矩阵乘积得:
(O,YT)(AOOB−CTA−1C)(OY)=(O,YT)(B−CTA−1C)(OY)
=YT(B−CTA−1C)Y.
故对任意
Y=O
,有
YT(B−CTA−1C)Y>0
,从而
B−CTA−1C
为正定矩阵。
22
(本题满分 13 分)
设二维随机变量
(X,Y)
的概率密度为
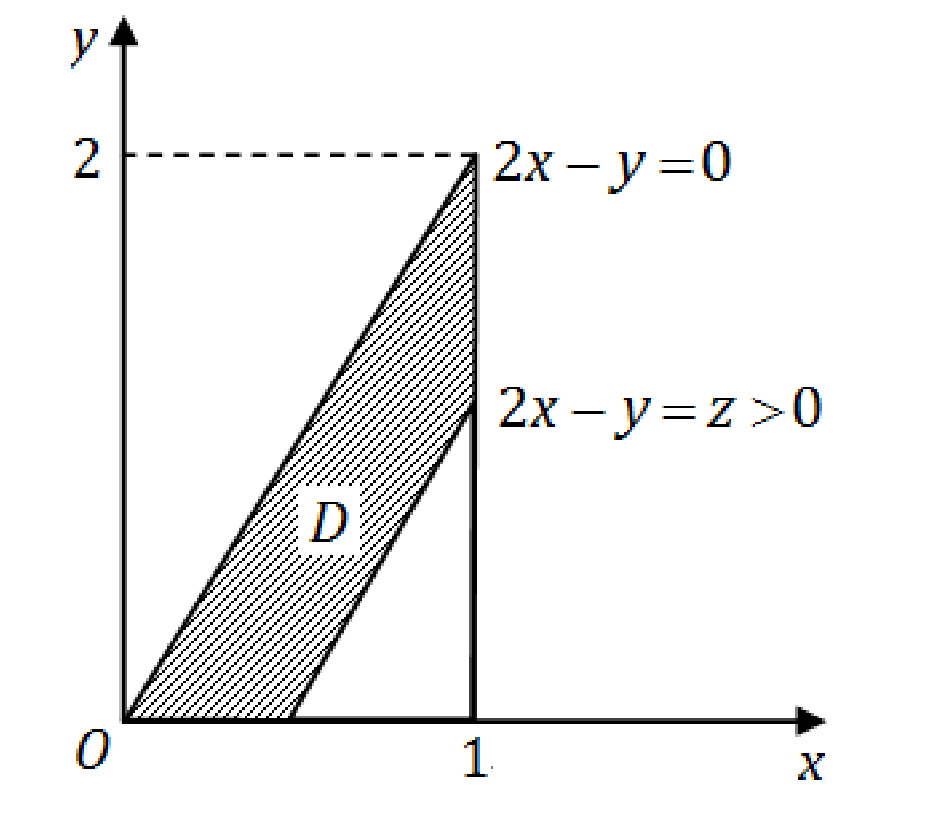
f(x,y)={1,0,0<x<1,0<y<2x,其他.
求:
(1)
(X,Y)
的边缘概率密度
fX(x),fY(y)
;
(2)
Z=2X−Y
的概率密度
fZ(z)
;
(3)
P{Y≤21X≤21}
.
【答案】
(1)
fX(x)={2x,0,0<x<1其他
,
fY(y)={1−2y,0,0<y<2其他
(2)
fZ(z)={1−2z,0,0<z<2其他
(3)
43
【解析】
(I) 由边缘密度函数的定义,关于
X
的边缘概率密度为:
fX(x)=∫−∞+∞f(x,y)dy=⎩⎨⎧∫02xdy,0,0<x<1,其他.={2x,0,0<x<1,其他. 关于
Y
的边缘概率密度:
fY(y)=∫−∞+∞f(x,y)dx=⎩⎨⎧∫2y1dx,0,0<y<2,其他.={1−2y,0,0<y<2,其他. (II) 由分布函数的定义:
FZ(z)=P{Z≤z}=P{2X−Y≤z}
。当
z<0
时,
FZ(z)=P{2X−Y≤z}=0
。当
z≥2
时,
FZ(z)=P{2X−Y≤z}=1
。当
0≤z<2
时,如图转换成阴影部分的二重积分。
FZ(z)=P{2X−Y≤z}=∬2x−y≤zf(x,y)dxdy
=1−∬2x−y>zf(x,y)dxdy=1−∫2z1dx∫02x−zdy=z−41z2.
所以分布函数为
FZ(z)=⎩⎨⎧0,z−41z2,1,z<0,0≤z<2,z≥2. 由密度函数与分布函数的关系,所求的概率密度为
fZ(z)={1−21z,0,0<z<2,其他.
(Ⅲ) 因为
P{X⩽21,Y⩽21}=∬x⩽21,y⩽21f(x,y)dxdy=∫021dy∫2y21dx=163,
P{X⩽21}=∫021fX(x)dx=∫0212xdx=41,
所以由条件概率公式得
P{Y⩽21X⩽21}=P{X⩽21}P{X⩽21,Y⩽21}=41163=43. 23
(本题满分 13 分)
设
X1,X2,⋯,Xn(n>2)
为来自总体
N(0,σ2)
的简单随机样本,
其样本均值为
X
,记
Yi=Xi−X
,
i=1,2,⋯,n
.
(1) 求
Yi
的方差
DYi
,
i=1,2,⋯,n
;
(2) 求
Y1
与
Yn
的协方差
Cov(Y1,Yn)
;
(3) 若
c(Y1+Yn)2
是
σ2
的无偏估计量,求常数
c
.
【答案】
(1)
DYi=nn−1σ2
(2)
Cov(Y1,Yn)=−nσ2
(3)
c=2(n−2)n
【解析】
由题设知
X1,X2,⋯,Xn(n>2)
相互独立,且
EXi=0,DXi=σ2(i=1,2,⋯,n)
,
EX=E(n1i=1∑nXi)=n1i=1∑nEXi=0,
DX=D(n1i=1∑nXi)=n21i=1∑nDXi=nσ2.
(I) 因为
Yi=Xi−X
,所以对
i=1,2,⋯,n
,有
EYi=0
,
DYi=D(Xi−X)=D(1−n1)Xi−n1j=i∑Xj =n2(n−1)2σ2+n21⋅(n−1)σ2=nn−1σ2.
(II) 由协方差的定义:
Cov(Y1,Yn)=E(Y1Yn)−EY1EYn=E(Y1Yn)
=E[(X1−X)(Xn−X)]=E(X1Xn−X1X−XnX+X2)
=E(X1Xn)−E(X1X)−E(XnX)+E(X2).
因为
X1,Xn
独立,有
E(X1Xn)=EX1EXn=0×0=0.
由方差的公式,有
E(X2)=DX+(EX)2=nσ2+0=nσ2.
由期望的性质和方差的公式有
E(X1X)=E(n1j=1∑nX1Xj)=E(n1X12+n1j=2∑nX1Xj)=n1E(X12)+n1j=2∑nEX1EXj=n1[DX1+(EX1)2]+0=n1(σ2+0)=nσ2.
同理
E(XnX)=nσ2
。所以
Cov(Y1,Yn)=E(X1Xn)−E(X1X)−E(XnX)+E(X2)=0−nσ2−nσ2+nσ2=−nσ2.
(Ⅲ) 由
c(Y1+Yn)2
是
σ2
的无偏估计量,则
E[c(Y1+Yn)2]=σ2
。而
E[c(Y1+Yn)2]=cE[(Y1+Yn)2]=c[D(Y1+Yn)+[E(Y1+Yn)]2]
又
E(Y1+Yn)=EY1+EYn=0
,
D(Y1+Yn)=DY1+DY2+2Cov(Y1,Yn)=nn−1σ2+nn−1σ2+2(−nσ2)=n2(n−2)σ2,
所以得到
E[c(Y1+Yn)2]=c[D(Y1+Yn)+[E(Y1+Yn)]2]=n2(n−2)cσ2.
由
E[c(Y1+Yn)2]=σ2
,得
n2(n−2)cσ2=σ2
,解得
c=2(n−2)n
。