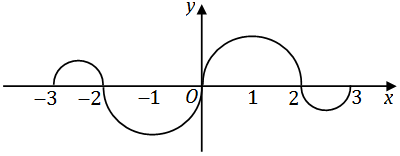卷 1

选择题

1～10小题，每小题4分，共40分

1

当 $x \to 0^+$ 时，与 $\sqrt{x}$ 等价的无穷小量是

高等数学函数、极限、连续无穷小量的比较

正确答案：B

【解析】 当 $x \to 0^+$ 时，需要找到与 $\sqrt{x}$ 等价的无穷小量，即求 $\lim_{x \to 0^+} \frac{f(x)}{\sqrt{x}} = 1$ 。

选项 A： $1 - e^{\sqrt{x}}$ ，计算极限 $\lim_{x \to 0^+} \frac{1 - e^{\sqrt{x}}}{\sqrt{x}} = -\lim_{t \to 0^+} \frac{e^t - 1}{t} = -1 \neq 1$ ，故不等价。
选项 B： $\ln \frac{1 + x}{1 - \sqrt{x}} = \ln(1 + x) - \ln(1 - \sqrt{x})$ ，计算极限 $\lim_{x \to 0^+} \frac{\ln \frac{1 + x}{1 - \sqrt{x}}}{\sqrt{x}} = \lim_{x \to 0^+} \frac{\ln(1 + x) - \ln(1 - \sqrt{x})}{\sqrt{x}}$ 。由于 $\ln(1 + x) \sim x$ ，且 $\frac{x}{\sqrt{x}} = \sqrt{x} \to 0$ ，而 $\ln(1 - \sqrt{x}) \sim -\sqrt{x}$ ，所以 $-\ln(1 - \sqrt{x}) \sim \sqrt{x}$ ，因此极限为 1，故等价。
选项 C： $\sqrt{1 + \sqrt{x}} - 1$ ，利用等价无穷小 $\sqrt{1 + u} - 1 \sim \frac{1}{2} u$ （当 $u \to 0$ ），令 $u = \sqrt{x}$ ，则 $\sqrt{1 + \sqrt{x}} - 1 \sim \frac{1}{2} \sqrt{x}$ ，极限为 $\frac{1}{2} \neq 1$ ，故不等价。
选项 D： $1 - \cos \sqrt{x}$ ，利用等价无穷小 $1 - \cos t \sim \frac{1}{2} t^2$ （当 $t \to 0$ ），令 $t = \sqrt{x}$ ，则 $1 - \cos \sqrt{x} \sim \frac{1}{2} x$ ，与 $\sqrt{x}$ 比较的极限为 $\frac{\frac{1}{2} x}{\sqrt{x}} = \frac{1}{2} \sqrt{x} \to 0$ ，故不等价。
因此，只有选项 B 与 $\sqrt{x}$ 等价。

2

曲线 $y = \frac{1}{x} + \ln(1 + \e^x)$ 渐近线的条数为

高等数学一元函数微分学曲线的凹凸性、拐点及渐近线

正确答案：D
【解析】 为了求曲线

y = \frac{1}{x} + \ln(1 + e^x)

的渐近线，需考虑水平渐近线、垂直渐近线和斜渐近线。
当

x \to -\infty

时，

\frac{1}{x} \to 0

，

\ln(1 + e^x) \to \ln(1) = 0

，因此

y \to 0

，有一条水平渐近线

y = 0

。
当

x \to 0

时，

\frac{1}{x} \to \infty

，而

\ln(1 + e^x)

有限，因此有一条垂直渐近线

x = 0

。
当

x \to +\infty

时，计算

\lim_{x \to +\infty} \frac{y}{x} = \lim_{x \to +\infty} \left( \frac{1}{x^2} + \frac{\ln(1 + e^x)}{x} \right) = 0 + 1 = 1

，且

\lim_{x \to +\infty} (y - x) = \lim_{x \to +\infty} \left( \frac{1}{x} + \ln(1 + e^x) - x \right) = \lim_{x \to +\infty} \ln(1 + e^{-x}) = \ln(1) = 0

，因此有一条斜渐近线

y = x

。
综上，曲线有三条渐近线，故答案为 D。

3

如图，连续函数 $y = f(x)$ 在区间 $[- 3, - 2]$ , $[2,3]$ 上的图形分别是直径为 $1$ 的上、下半圆周，在区间 $[- 2,0]$ , $[0,2]$ 上图形分别是直径为 $2$ 的上、下半圆周．

设 $F(x) = \int_0^x f(t) \dt$ ，则下列结论正确的是

高等数学一元函数积分学变限积分

正确答案：C

【解析】 由所给条件知， $f(x)$ 为 $x$ 的奇函数，则 $f(-x) = -f(x)$ ，由 $F(x) = \int_{0}^{x} f(t) dt$ 知

F(-x) = \int_{0}^{-x} f(t) dt = \int_{0}^{x} f(-u) d(-u) = \int_{0}^{x} f(u) du = F(x),

故 $F(x)$ 为 $x$ 的偶函数，所以 $F(-3) = F(3)$ 。由于曲线由半圆周组成，由定积分的几何意义，得到

F(2) = \int_{0}^{2} f(t) dt = \frac{\pi}{2} \cdot 1^2 = \frac{\pi}{2},

F(3) = \int_{0}^{3} f(t) dt = \int_{0}^{2} f(t) dt + \int_{2}^{3} f(t) dt = \frac{\pi}{2} \cdot 1^2 - \frac{\pi}{2} \cdot \left(\frac{1}{2}\right)^2 = \frac{\pi}{2} \cdot \frac{3}{4} = \frac{3}{4} F(2).

所以 $F(-3) = F(3) = \frac{3}{4} F(2)$ 。

4

设函数 $f(x)$ 在 $x = 0$ 连续，则下列命题错误的是

高等数学函数、极限、连续函数的连续性

正确答案：D

【解析】

应选 (D)。例如取 $f(x) = |x|$ ，有

\lim_{x \to 0} \frac{f(x) - f(-x)}{x - 0} = \lim_{x \to 0} \frac{|x| - |-x|}{x} = 0

存在，而

\lim_{x \to 0^-} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^-} \frac{-x - 0}{x - 0} = -1, \quad \lim_{x \to 0^+} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0^+} \frac{x - 0}{x - 0} = 1,

左右极限存在但不相等，所以 $f(x) = |x|$ 在 $x = 0$ 的导数 $f'(0)$ 不存在，即选项 (D) 错误。

由 $\lim_{x \to 0} \frac{f(x)}{x}$ 存在及 $f(x)$ 在 $x = 0$ 处连续，可得

f(0) = \lim_{x \to 0} f(x) = \lim_{x \to 0} \left( \frac{f(x)}{x} \cdot x \right) = \lim_{x \to 0} \frac{f(x)}{x} \cdot \lim_{x \to 0} x = 0 \cdot \lim_{x \to 0} \frac{f(x)}{x} = 0,

所以选项 (A) 正确。

由选项 (A) 知 $f(0) = 0$ ，所以

f'(0) = \lim_{x \to 0} \frac{f(x) - f(0)}{x - 0} = \lim_{x \to 0} \frac{f(x)}{x}

存在，所以选项 (C) 也正确。

由 $f(x)$ 在 $x = 0$ 处连续，所以 $f(-x)$ 在 $x = 0$ 处连续，从而

\lim_{x \to 0} [f(x) + f(-x)] = \lim_{x \to 0} f(x) + \lim_{x \to 0} f(-x) = f(0) + f(0) = 2f(0),

所以

2f(0) = \lim_{x \to 0} \left[ \frac{f(x) + f(-x)}{x} \cdot x \right] = \lim_{x \to 0} \frac{f(x) + f(-x)}{x} \cdot \lim_{x \to 0} x = 0 \cdot \lim_{x \to 0} \frac{f(x) + f(-x)}{x} = 0,

即有 $f(0) = 0$ ，所以选项 (B) 正确。

5

设函数 $f(x)$ 在 $(0, +\infty)$ 上具有二阶导数，且 $f''(x) > 0$ ，令 $u_n = f(n)$ （ $n=1,2,\cdots$ ），则下列结论正确的是

高等数学一元函数微分学微分中值定理

正确答案：D

【解析】 函数 $f(x)$ 在 $(0, +\infty)$ 上具有二阶导数，且 $f''(x) > 0$ ，因此 $f(x)$ 是凸函数，且 $f'(x)$ 单调递增。令 $u_n = f(n)$ ，考虑选项条件。

若 $u_1 < u_2$ ，即 $f(1) < f(2)$ ，由微分中值定理，存在 $c \in (1,2)$ 使得 $f'(c) = \frac{f(2)-f(1)}{2-1} > 0$ 。由于 $f'(x)$ 单调递增，对任意 $x > c$ ，有 $f'(x) > f'(c) > 0$ 。因此，当 $x \geq 2$ 时， $f'(x) > 0$ ，且 $f'(x)$ 有正下界，故 $f(x)$ 在 $[2, +\infty)$ 上严格递增且至少以线性速度增长，从而 $\lim_{x \to \infty} f(x) = +\infty$ ，序列 $\{u_n\}$ 发散。

对于其他选项，反例表明不一定成立：

若 $u_1 > u_2$ ，如 $f(x) = \frac{1}{x}$ ，则 $u_n = \frac{1}{n}$ 收敛；如 $f(x) = -\ln x$ ，则 $u_n = -\ln n$ 发散。故 A 和 B 错误。
若 $u_1 < u_2$ ，如 $f(x) = x^2$ ，则 $u_n = n^2$ 发散，故 C 错误。

因此，正确结论为 D。

6

设曲线 $L:f(x,y) = 1$ （ $f(x,y)$ 具有一阶连续偏导数）过第Ⅱ象限内的点 $M$ 和第Ⅳ象限内的点 $N$ ， $\Gamma$ 为 $L$ 上从点 $M$ 到点 $N$ 的一段弧，则下列积分小于零的是

多元函数积分学第二类曲线积分

正确答案：B
【解析】 曲线

L: f(x,y) = 1

上，

f(x,y)

恒为 1。点

M

在第 II 象限（

x < 0, y > 0

），点

N

在第 IV 象限（

x > 0, y < 0

），弧

\Gamma

从

M

到

N

。
对于选项 A：

\int_{\Gamma} f(x,y) \, dx = \int_{\Gamma} 1 \, dx = x(N) - x(M)

。由于

x(N) > 0

，

x(M) < 0

，因此

x(N) - x(M) > 0

，积分大于零。
对于选项 B：

\int_{\Gamma} f(x,y) \, dy = \int_{\Gamma} 1 \, dy = y(N) - y(M)

。由于

y(N) < 0

，

y(M) > 0

，因此

y(N) - y(M) < 0

，积分小于零。
对于选项 C：

\int_{\Gamma} f(x,y) \, ds = \int_{\Gamma} 1 \, ds

，其中

ds

为弧长元素，始终为正，因此积分大于零。
对于选项 D：

\int_{\Gamma} f'_x(x,y) \, dx + f'_y(x,y) \, dy = \int_{\Gamma} df(x,y)

。由于在曲线

L

上

f(x,y) = 1

为常数，故

df(x,y) = 0

，积分等于零。
因此，只有选项 B 的积分小于零。

7

设向量组 $\alpha_1$ , $\alpha_2$ , $\alpha_3$ 线性无关，则下列向量组线性相关的是

线性代数向量向量组的线性相关性

正确答案：A

【解析】

应选 (A). 因为 $(\alpha_1 - \alpha_2) + (\alpha_2 - \alpha_3) + (\alpha_3 - \alpha_1) = 0$ , 所以 $\alpha_1 - \alpha_2, \alpha_2 - \alpha_3, \alpha_3 - \alpha_1$ 线性相关.

选项 (B) 不对. 因为

(\alpha_1 + \alpha_2, \alpha_2 + \alpha_3, \alpha_3 + \alpha_1) = (\alpha_1, \alpha_2, \alpha_3) \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} = (\alpha_1, \alpha_2, \alpha_3)P_2,

其中 $|P_2| = 2 \neq 0$ .

选项 (C) 不对, 因为

(\alpha_1 - 2\alpha_2, \alpha_2 - 2\alpha_3, \alpha_3 - 2\alpha_1) = (\alpha_1, \alpha_2, \alpha_3) \begin{pmatrix} 1 & 0 & -2 \\ -2 & 1 & 0 \\ 0 & -2 & 1 \end{pmatrix} = (\alpha_1, \alpha_2, \alpha_3)P_3,

其中 $|P_3| = -7 \neq 0$ .

选项 (D) 不对, 因为

(\alpha_1 + 2\alpha_2, \alpha_2 + 2\alpha_3, \alpha_3 + 2\alpha_1) = (\alpha_1, \alpha_2, \alpha_3) \begin{pmatrix} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 0 & 2 & 1 \end{pmatrix} = (\alpha_1, \alpha_2, \alpha_3)P_4,

其中 $|P_4| = 9 \neq 0$ .

8

设矩阵 $A = \begin{pmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{pmatrix}$ ， $B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}$ ，则 $A$ 与 $B$

线性代数矩阵的特征值与特征向量

正确答案：B

【解析】 矩阵 $A$ 的特征值为 $0, 3, 3$ ，矩阵 $B$ 的特征值为 $1, 1, 0$ 。由于特征值不同，因此 $A$ 与 $B$ 不相似。

$A$ 与 $B$ 都是实对称矩阵，且它们的正惯性指数均为 $2$ ，负惯性指数均为 $0$ ，因此 $A$ 与 $B$ 合同。

故 $A$ 与 $B$ 合同但不相似。

9

某人向同一目标独立重复射击，每次射击命中目标的概率为 $p$ （ $0 < p < 1$ ），则此人第 $4$ 次射击恰好第 $2$ 次命中目标的概率为

概率论与数理统计随机变量及其分布

正确答案：C
【解析】 第4次射击恰好第2次命中目标意味着在前三次射击中恰好有一次命中目标，且第四次射击命中目标。前三次射击中恰好一次命中的概率为

\binom{3}{1} p (1-p)^2 = 3p(1-p)^2

，第四次命中的概率为

p

。因此，总概率为

3p(1-p)^2 \times p = 3p^2(1-p)^2

，对应选项C。

10

设随机变量 $(X,Y)$ 服从二维正态分布，且 $X$ 与 $Y$ 不相关， $f_X(x),f_Y(y)$ 分别表示 $X,Y$ 的概率密度，则在 $Y = y$ 条件下， $X$ 的条件概率密度 $f_{X\left| Y \right.}(x\left| y) \right.$ 为

概率论与数理统计多维随机变量及其分布边缘分布和条件分布

正确答案：A
【解析】 由于随机变量

(X,Y)

服从二维正态分布，且

X

与

Y

不相关，在二维正态分布中，不相关等价于独立。因此，

X

与

Y

相互独立，联合概率密度函数

f_{X,Y}(x,y) = f_X(x) f_Y(y)

。条件概率密度

f_{X|Y}(x|y)

的定义为

f_{X|Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_Y(y)}

。代入独立条件，得

f_{X|Y}(x|y) = \frac{f_X(x) f_Y(y)}{f_Y(y)} = f_X(x)

，故答案为A。

填空题

11～16小题，每小题4分，共24分

11

$\int_1^2\frac{1}{x^3} \e^{\frac{1}{x}} \dx =$ ______．

高等数学一元函数积分学定积分的计算

【答案】
$\frac{1}{2} \sqrt{e}$

【解析】
考虑积分 $\int_1^2 \frac{1}{x^3} e^{\frac{1}{x}} \, dx$ 。令 $u = \frac{1}{x}$ ，则 $du = -\frac{1}{x^2} \, dx$ 。当 $x = 1$ 时， $u = 1$ ；当 $x = 2$ 时， $u = \frac{1}{2}$ 。
被积函数可写为：

\frac{1}{x^3} e^{\frac{1}{x}} \, dx = u^3 e^u \cdot \left( -\frac{1}{u^2} \, du \right) = -u e^u \, du

因此，积分变为：

\int_1^2 \frac{1}{x^3} e^{\frac{1}{x}} \, dx = \int_1^{\frac{1}{2}} -u e^u \, du = \int_{\frac{1}{2}}^1 u e^u \, du

计算 $\int u e^u \, du$ 使用分部积分法：
令 $f = u$ ， $g' = e^u$ ，则 $f' = 1$ ， $g = e^u$ ，

\int u e^u \, du = u e^u - \int e^u \, du = u e^u - e^u + C = e^u (u - 1) + C

代入上下限：

\int_{\frac{1}{2}}^1 u e^u \, du = \left[ e^u (u - 1) \right]_{\frac{1}{2}}^1 = \left( e^1 (1 - 1) \right) - \left( e^{\frac{1}{2}} \left( \frac{1}{2} - 1 \right) \right) = 0 - \left( e^{\frac{1}{2}} \cdot \left( -\frac{1}{2} \right) \right) = \frac{1}{2} e^{\frac{1}{2}} = \frac{1}{2} \sqrt{e}

故原积分的值为 $\frac{1}{2} \sqrt{e}$ 。

12

设 $f(u,v)$ 为二元可微函数， $z = f(x^y,y^x)$ ，则 $\frac{\pdz}{\pdx} =$ ______．

高等数学多元函数微分学偏导数的概念与计算

【答案】

\frac{\partial z}{\partial x} = \frac{\partial f}{\partial u} \cdot y x^{y-1} + \frac{\partial f}{\partial v} \cdot y^x \ln y

其中偏导数 $\frac{\partial f}{\partial u}$ 和 $\frac{\partial f}{\partial v}$ 在点 $(u,v) = (x^y, y^x)$ 处取值。

【解析】 给定 $z = f(x^y, y^x)$ ，其中 $f(u,v)$ 是二元可微函数。令 $u = x^y$ 和 $v = y^x$ ，则 $z = f(u, v)$ 。使用链式法则求 $\frac{\partial z}{\partial x}$ ：

\frac{\partial z}{\partial x} = \frac{\partial f}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial f}{\partial v} \frac{\partial v}{\partial x}.

计算 $\frac{\partial u}{\partial x}$ ：由于 $u = x^y$ ，且 $y$ 视为常数，有 $\frac{\partial u}{\partial x} = y x^{y-1}$ 。计算 $\frac{\partial v}{\partial x}$ ：由于 $v = y^x$ ，且 $y$ 视为常数，有 $\frac{\partial v}{\partial x} = y^x \ln y$ 。代入链式法则公式，得到：

\frac{\partial z}{\partial x} = \frac{\partial f}{\partial u} \cdot y x^{y-1} + \frac{\partial f}{\partial v} \cdot y^x \ln y.

其中 $\frac{\partial f}{\partial u}$ 和 $\frac{\partial f}{\partial v}$ 在点 $(u,v) = (x^y, y^x)$ 处计算。

13

二阶常系数非齐次线性微分方程 $y'' - 4y' + 3y = 2\e^{2x}$ 的通解为 $y=$ ______．

高等数学常微分方程常系数非齐次线性微分方程

【答案】
$y = C_1 e^{3x} + C_2 e^{x} - 2 e^{2x}$

【解析】
给定二阶常系数非齐次线性微分方程 $y'' - 4y' + 3y = 2e^{2x}$ ，首先求解齐次方程 $y'' - 4y' + 3y = 0$ 。
特征方程为 $r^2 - 4r + 3 = 0$ ，解得 $r_1 = 3$ ， $r_2 = 1$ ，因此齐次通解为 $y_h = C_1 e^{3x} + C_2 e^{x}$ 。
由于非齐次项为 $2e^{2x}$ ，且 $2$ 不是特征根，设特解形式为 $y_p = A e^{2x}$ 。
代入原方程：
$y_p' = 2A e^{2x}$ ， $y_p'' = 4A e^{2x}$ ，
则 $y_p'' - 4y_p' + 3y_p = 4A e^{2x} - 8A e^{2x} + 3A e^{2x} = -A e^{2x}$ 。
令其等于 $2e^{2x}$ ，得 $-A = 2$ ，即 $A = -2$ ，故特解为 $y_p = -2 e^{2x}$ 。
因此，通解为齐次通解与特解之和： $y = y_h + y_p = C_1 e^{3x} + C_2 e^{x} - 2 e^{2x}$ 。

14

设曲面 $\Sigma :|x| + |y| + |z| = 1$ ，则 $\oiint_{\Sigma}(x + |y|) \dS =$ ______．

多元函数积分学第二类曲面积分

【答案】

\frac{4\sqrt{3}}{3}

【解析】 首先，计算曲面积分 $\oiint_{\Sigma}(x + |y|) \dS$ ，其中曲面 $\Sigma: |x| + |y| + |z| = 1$ 。
由于曲面关于 $yz$ 平面对称，且 $x$ 是奇函数，因此 $\oiint_{\Sigma} x \dS = 0$ 。
于是，积分简化为 $\oiint_{\Sigma} |y| \dS$ 。
接下来，计算 $\oiint_{\Sigma} |y| \dS$ 。
由曲面的对称性，有 $\oiint_{\Sigma} |x| \dS = \oiint_{\Sigma} |y| \dS = \oiint_{\Sigma} |z| \dS$ 。
在曲面上， $|x| + |y| + |z| = 1$ ，因此

\oiint_{\Sigma} (|x| + |y| + |z|) \dS = \oiint_{\Sigma} 1 \dS = A,

其中 $A$ 是曲面的表面积。
曲面 $\Sigma$ 是一个正八面体，由 8 个等边三角形面组成，每个三角形的边长为 $\sqrt{2}$ ，面积为 $\frac{\sqrt{3}}{2}$ ，故总表面积 $A = 8 \times \frac{\sqrt{3}}{2} = 4\sqrt{3}$ 。
于是，

\oiint_{\Sigma} |y| \dS = \frac{A}{3} = \frac{4\sqrt{3}}{3}.

因此，

\oiint_{\Sigma} (x + |y|) \dS = 0 + \frac{4\sqrt{3}}{3} = \frac{4\sqrt{3}}{3}.

15

设矩阵 $A = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ ，则 $A^3$ 的秩为______．

线性代数矩阵矩阵的秩

【答案】 $1$

【解析】
矩阵 $A = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ 是一个移位矩阵。计算 $A^3$ ：
首先， $A^2 = A \times A = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ 。
然后， $A^3 = A^2 \times A = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ 。
矩阵 $A^3$ 只有第一行非零，且该行为 $(0,0,0,1)$ ，因此行秩为1；同样，只有第四列非零，列秩也为1。故 $A^3$ 的秩为1。

16

在区间 $(0,1)$ 中随机地取两个数，则这两数之差的绝对值小于 $\frac{1}{2}$ 的概率为______．

概率论与数理统计随机事件和概率

【答案】 $\frac{3}{4}$

【解析】 在区间 $(0,1)$ 中随机取两个数 $x$ 和 $y$ ，则点 $(x,y)$ 落在单位正方形 $[0,1] \times [0,1]$ 内。总面积为1。需要求 $|x-y| < \frac{1}{2}$ 的概率，即满足条件的区域面积。

条件 $|x-y| < \frac{1}{2}$ 等价于 $-\frac{1}{2} < x-y < \frac{1}{2}$ ，即 $y - \frac{1}{2} < x < y + \frac{1}{2}$ 。在单位正方形内，该区域由两条直线 $x-y = \frac{1}{2}$ 和 $x-y = -\frac{1}{2}$ 界定。

不满足条件的区域为 $|x-y| \geq \frac{1}{2}$ ，包括两个三角形：

当 $x-y \geq \frac{1}{2}$ 时，区域为三角形，顶点为 $(1/2,0)$ 、 $(1,0)$ 、 $(1,1/2)$ ，面积为 $\frac{1}{8}$ 。
当 $x-y \leq -\frac{1}{2}$ 时，区域为三角形，顶点为 $(0,1/2)$ 、 $(0,1)$ 、 $(1/2,1)$ ，面积为 $\frac{1}{8}$ 。

不满足条件的区域总面积为 $\frac{1}{8} + \frac{1}{8} = \frac{1}{4}$ ，因此满足条件的区域面积为 $1 - \frac{1}{4} = \frac{3}{4}$ 。

或者，通过积分计算：对于固定 $y$ ， $x$ 的允许长度为 $\min(1, y+1/2) - \max(0, y-1/2)$ 。

当 $y \in [0, 1/2]$ 时，长度为 $(y + 1/2) - 0 = y + 1/2$ 。
当 $y \in [1/2, 1]$ 时，长度为 $1 - (y - 1/2) = 3/2 - y$ 。积分得： $\int_{0}^{1/2} (y + 1/2) \, dy = \frac{3}{8}, \quad \int_{1/2}^{1} (3/2 - y) \, dy = \frac{3}{8},$ 总和为 $\frac{3}{4}$ 。

故概率为 $\frac{3}{4}$ 。

解答题

17～24小题，共86分

17

（本题满分 10 分）

求函数 $f(x,y) = x^2 + 2y^2 - x^2y^2$ 在区域 $D = \left\{(x,y)\left| x^2 + y^2 \le 4,y \ge 0 \right. \right\}$ 上的最大值和最小值．

高等数学多元函数微分学多元函数的极值问题

【答案】 最小值：0，最大值：8

【解析】 首先，求函数在区域内部的临界点。计算偏导数 $f_x = 2x - 2x y^2$ 和 $f_y = 4y - 2x^2 y$ ，令其为零：

$f_x = 0$ 得 $x = 0$ 或 $y^2 = 1$ ；
$f_y = 0$ 得 $y = 0$ 或 $x^2 = 2$ 。结合条件，得临界点 $(0,0)$ 、 $(\sqrt{2},1)$ 和 $(-\sqrt{2},1)$ ，函数值分别为 $0$ 、 $2$ 和 $2$ 。

其次，考虑边界。边界由 $y = 0$ （ $-2 \leq x \leq 2$ ）和半圆 $x^2 + y^2 = 4$ （ $y \geq 0$ ）组成：

在 $y = 0$ 上，函数化为 $f(x,0) = x^2$ ，最小值为 $0$ （在 $(0,0)$ ），最大值为 $4$ （在 $(\pm 2,0)$ ）。
在半圆上，代入 $x^2 = 4 - y^2$ 得 $f(x,y) = 4 - 3y^2 + y^4$ 。令 $g(y) = y^4 - 3y^2 + 4$ （ $y \in [0,2]$ ），求导 $g'(y) = 4y^3 - 6y$ ，得临界点 $y = 0$ 和 $y = \sqrt{3/2}$ 。函数值：在 $y = 0$ 时 $f = 4$ ，在 $y = \sqrt{3/2}$ 时 $f = 7/4$ ，在 $y = 2$ 时 $f = 8$ .

比较所有点函数值：内部临界点值 $0$ 和 $2$ ，边界值 $0$ 、 $4$ 、 $7/4$ 、 $8$ ，故最小值为 $0$ ，最大值为 $8$ 。

18

（本题满分 11 分）

计算曲面积分 $I = \iint_{\Sigma}xz\dy\dz + 2zy\dz\dx + 3xy \dx\dy$ ，其中 $\Sigma$ 为曲面 $z = 1 - x^2 - \frac{y^2}{4}$ （ $0 \le z \le 1$ ）的上侧．

高等数学多元函数积分学第二类曲面积分

【答案】 $\pi$

【解析】 考虑使用高斯散度定理。曲面 $\Sigma$ 是开放曲面，需添加底面 $\Sigma_1: z=0, x^2 + \frac{y^2}{4} \leq 1$ 取下侧，构成封闭曲面 $S = \Sigma \cup \Sigma_1$ 。设向量场 $\vec{F} = (P, Q, R) = (xz, 2zy, 3xy)$ ，则原积分可写为：

I = \iint_{\Sigma} P \, dy \, dz + Q \, dz \, dx + R \, dx \, dy.

由高斯定理：

\iint_{S} P \, dy \, dz + Q \, dz \, dx + R \, dx \, dy = \iiint_{V} \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right) dV,

其中 $V$ 是 $S$ 所围成的区域。计算散度：

\frac{\partial P}{\partial x} = \frac{\partial}{\partial x}(xz) = z, \quad \frac{\partial Q}{\partial y} = \frac{\partial}{\partial y}(2zy) = 2z, \quad \frac{\partial R}{\partial z} = \frac{\partial}{\partial z}(3xy) = 0,

所以 $\nabla \cdot \vec{F} = z + 2z + 0 = 3z$ 。因此：

\iint_{S} \vec{F} \cdot d\vec{S} = \iiint_{V} 3z \, dV.

区域 $V$ 由 $0 \leq z \leq 1 - x^2 - \frac{y^2}{4}$ 和 $x^2 + \frac{y^2}{4} \leq 1$ 定义。采用坐标变换：令 $x = r \cos \theta, y = 2r \sin \theta$ ，则雅可比行列式为 $2r$ ，即 $dx \, dy = 2r \, dr \, d\theta$ ，且 $r \leq 1, \theta \in [0, 2\pi]$ 。于是：

\iiint_{V} 3z \, dV = \int_{0}^{2\pi} \int_{0}^{1} \int_{0}^{1 - r^2} 3z \cdot 2r \, dz \, dr \, d\theta = \int_{0}^{2\pi} \int_{0}^{1} 6r \left[ \frac{1}{2} z^2 \right]_{0}^{1 - r^2} dr \, d\theta = \int_{0}^{2\pi} \int_{0}^{1} 3r (1 - r^2)^2 \, dr \, d\theta.

计算内积分：

\int_{0}^{1} 3r (1 - r^2)^2 \, dr = 3 \int_{0}^{1} r (1 - 2r^2 + r^4) \, dr = 3 \left[ \frac{1}{2} r^2 - \frac{1}{2} r^4 + \frac{1}{6} r^6 \right]_{0}^{1} = 3 \left( \frac{1}{2} - \frac{1}{2} + \frac{1}{6} \right) = \frac{1}{2}.

所以：

\iiint_{V} 3z \, dV = \int_{0}^{2\pi} \frac{1}{2} \, d\theta = \pi.

即：

\iint_{S} \vec{F} \cdot d\vec{S} = \pi.

现在计算底面 $\Sigma_1$ 的积分。在 $\Sigma_1$ 上， $z=0$ ，取法向量向下 $\vec{n} = (0,0,-1)$ ，则：

\iint_{\Sigma_1} \vec{F} \cdot d\vec{S} = \iint_{\Sigma_1} (xz, 2zy, 3xy) \cdot (0,0,-1) \, dS = \iint_{D} -3xy \, dx \, dy,

其中 $D: x^2 + \frac{y^2}{4} \leq 1$ 。由于被积函数 $xy$ 在 $D$ 上关于 $x$ 和 $y$ 均为奇函数，且 $D$ 对称，故积分值为零：

\iint_{D} -3xy \, dx \, dy = 0.

因此：

\iint_{\Sigma} \vec{F} \cdot d\vec{S} = \iint_{S} \vec{F} \cdot d\vec{S} - \iint_{\Sigma_1} \vec{F} \cdot d\vec{S} = \pi - 0 = \pi.

故原积分 $I = \pi$ 。

19

（本题满分 11 分）

设函数 $f(x)$ ， $g(x)$ 在 $\;\left[a,b \right]$ 上连续，在 $(a,b)$ 内二阶可导且存在相等的最大值，又 $f(a)$ = $g(a)$ ， $f(b)$ = $g(b)$ ，证明：存在 $\xi \in(a,b)$ ，使得 $f''(\xi) = g''(\xi)$ ．

高等数学一元函数微分学微分中值定理

【答案】
存在 $\xi \in (a,b)$ ，使得 $f''(\xi) = g''(\xi)$ 。

【解析】
令 $\varphi(x) = f(x) - g(x)$ ，由题设 $f(x), \, g(x)$ 存在相等的最大值，设 $x_1 \in (a, b), \, x_2 \in (a, b)$ 使得

f(x_1) = \max_{[a, b]} f(x) = g(x_2) = \max_{[a, b]} g(x).

于是 $\varphi(x_1) = f(x_1) - g(x_1) \geq 0, \, \varphi(x_2) = f(x_2) - g(x_2) \leq 0.$

若 $\varphi(x_1) = 0$ ，则取 $\eta = x_1 \in (a, b)$ ，有 $\varphi(\eta) = 0$ .

若 $\varphi(x_2) = 0$ ，则取 $\eta = x_2 \in (a, b)$ ，有 $\varphi(\eta) = 0$ .

若 $\varphi(x_1) > 0, \, \varphi(x_2) < 0$ ，则由连续函数介值定理知，存在 $\eta \in (x_1, x_2)$ 使 $\varphi(\eta) = 0$ . 不论以上哪种情况，总存在 $\eta \in (a, b)$ ，使 $\varphi(\eta) = 0$ . 另外有

\varphi(a) = f(a) - g(a) = 0, \, \varphi(b) = f(b) - g(b) = 0.

将 $\varphi(x)$ 在区间 $[a, \eta], [\eta, b]$ 分别应用罗尔定理，得存在 $\xi_1 \in (a, \eta), \xi_2 \in (\eta, b)$ ，使得 $\varphi'(\xi_1) = 0, \, \varphi'(\xi_2) = 0$ ；再由罗尔定理知，存在 $\xi \in (\xi_1, \xi_2)$ ，使 $\varphi''(\xi) = 0$ ，即有 $f''(\xi) = g''(\xi)$ .

20

（本题满分 10 分）

设幂级数 $\sum_{n = 0}^{\infty}a_n x^n$ 在 $(-\infty , +\infty)$ 内收敛，其和函数 $y(x)$ 满足

y'' - 2xy' - 4y = 0,y(0) = 0,y'(0) = 1.

(1) 证明 $a_{n + 2} = \frac{2}{n + 1}a_n,\;n = 1,2, \cdots$ ；

(2) 求 $y(x)$ 的表达式．

高等数学无穷级数幂级数的和函数及幂级数展开式

【答案】
(1) 证明见解析。
(2) $y(x) = x e^{x^2}$

【解析】
(1) 设 $y(x) = \sum_{n=0}^{\infty} a_n x^n$ ，则 $y'(x) = \sum_{n=1}^{\infty} n a_n x^{n-1}$ ， $y''(x) = \sum_{n=2}^{\infty} n(n-1) a_n x^{n-2}$ 。代入微分方程 $y'' - 2xy' - 4y = 0$ ，得：

\sum_{n=2}^{\infty} n(n-1) a_n x^{n-2} - 2x \sum_{n=1}^{\infty} n a_n x^{n-1} - 4 \sum_{n=0}^{\infty} a_n x^n = 0

调整索引：第一项为 $\sum_{n=0}^{\infty} (n+2)(n+1) a_{n+2} x^n$ ，第二项为 $-2 \sum_{n=0}^{\infty} n a_n x^n$ （当 $n=0$ 时项为 0），第三项为 $-4 \sum_{n=0}^{\infty} a_n x^n$ 。合并得：

\sum_{n=0}^{\infty} \left[ (n+2)(n+1) a_{n+2} - 2n a_n - 4 a_n \right] x^n = 0

即

\sum_{n=0}^{\infty} \left[ (n+2)(n+1) a_{n+2} - 2(n+2) a_n \right] x^n = 0

由于级数恒为零，系数必为零：

(n+2)(n+1) a_{n+2} - 2(n+2) a_n = 0

对于 $n \geq 0$ ，由于 $n+2 \neq 0$ ，除以 $n+2$ 得：

(n+1) a_{n+2} = 2 a_n

即

a_{n+2} = \frac{2}{n+1} a_n

对于 $n = 1, 2, \cdots$ ，该式成立。

(2) 由初始条件 $y(0) = 0$ 得 $a_0 = 0$ ，由 $y'(0) = 1$ 得 $a_1 = 1$ 。利用递推关系 $a_{n+2} = \frac{2}{n+1} a_n$ ：

当 $n$ 为偶数时， $a_0 = 0$ ，故所有偶数项 $a_{2k} = 0$ 。
当 $n$ 为奇数时， $a_1 = 1$ ， $a_3 = \frac{2}{2} a_1 = 1$ ， $a_5 = \frac{2}{4} a_3 = \frac{1}{2}$ ， $a_7 = \frac{2}{6} a_5 = \frac{1}{6}$ ，归纳得 $a_{2k+1} = \frac{1}{k!}$ 。
因此和函数为：
$y(x) = \sum_{k=0}^{\infty} a_{2k+1} x^{2k+1} = \sum_{k=0}^{\infty} \frac{1}{k!} x^{2k+1} = x \sum_{k=0}^{\infty} \frac{(x^2)^k}{k!} = x e^{x^2}$ 故 $y(x) = x e^{x^2}$ 。

21

（本题满分 11 分）

设线性方程组① $\begin{cases} x_1 + x_2 + x_3 = 0 \\ x_1 + 2x_2 + ax_3 = 0 \\ x_1 + 4x_2 + a^2x_3 = 0 \end{cases}$ 与方程② $x_1 + 2x_2 + x_3 = a - 1$ 有公共解，求 $a$ 的值及所有公共解．

线性代数线性方程组

【答案】
当 $a = 1$ 时，所有公共解为 $x_1 = -k, x_2 = 0, x_3 = k$ ，其中 $k$ 为任意常数；
当 $a = 2$ 时，公共解为 $x_1 = 0, x_2 = 1, x_3 = -1$ 。

【解析】
线性方程组①的系数矩阵行列式为：

\det\begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & a \\ 1 & 4 & a^2 \end{pmatrix} = (a-1)(a-2)

当 $a \neq 1$ 且 $a \neq 2$ 时，方程组①仅有零解，但零解代入方程②得 $0 = a-1$ ，要求 $a=1$ ，矛盾，故无公共解。
当 $a = 1$ 时，方程组①化为：

\begin{cases} x_1 + x_2 + x_3 = 0 \\ x_1 + 2x_2 + x_3 = 0 \\ x_1 + 4x_2 + x_3 = 0 \end{cases}

解得 $x_2 = 0$ ， $x_1 = -x_3$ ，令 $x_3 = k$ ，则解为 $x_1 = -k, x_2 = 0, x_3 = k$ 。代入方程② $x_1 + 2x_2 + x_3 = a-1 = 0$ ，得 $(-k) + 0 + k = 0$ ，恒成立，故所有解均为公共解。
当 $a = 2$ 时，方程组①化为：

\begin{cases} x_1 + x_2 + x_3 = 0 \\ x_1 + 2x_2 + 2x_3 = 0 \\ x_1 + 4x_2 + 4x_3 = 0 \end{cases}

解得 $x_1 = 0$ ， $x_2 = -x_3$ ，令 $x_3 = k$ ，则解为 $x_1 = 0, x_2 = -k, x_3 = k$ 。代入方程② $x_1 + 2x_2 + x_3 = a-1 = 1$ ，得 $0 + 2(-k) + k = -k = 1$ ，解得 $k = -1$ ，故公共解为 $x_1 = 0, x_2 = 1, x_3 = -1$ 。

22

（本题满分 11 分）

设 $3$ 阶实对称矩阵 $A$ 的特征值 $\lambda_1 = 1$ , $\lambda_2 = 2$ , $\lambda_3 = - 2$ ， $\alpha_1 = (1, - 1,1)^T$ 是 $A$ 的属于 $\lambda_1$ 的一个特征向量，记 $B = A^5 - 4A^3 + E$ ，其中 $E$ 为 $3$ 阶单位矩阵．

(1) 验证 $\alpha_1$ 是矩阵 $B$ 的特征向量，并求 $B$ 的全部特征值与特征向量；

(2) 求矩阵 $B$ ．

线性代数矩阵的特征值与特征向量

【答案】
(1) $\alpha_1$ 是矩阵 $B$ 的特征向量，对应的特征值为 $-2$ 。 $B$ 的全部特征值为 $-2, 1, 1$ 。特征向量：对于特征值 $-2$ ，特征向量为 $k\alpha_1$ （ $k \neq 0$ ）；对于特征值 $1$ ，特征向量为所有满足 $x_1 - x_2 + x_3 = 0$ 的向量 $x$ 。
(2) 矩阵 $B$ 为

B = \begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix}

【解析】
(1) 由于 $A$ 是实对称矩阵， $\alpha_1$ 是 $A$ 的属于特征值 $\lambda_1 = 1$ 的特征向量，即 $A\alpha_1 = \alpha_1$ 。则

B\alpha_1 = (A^5 - 4A^3 + E)\alpha_1 = A^5\alpha_1 - 4A^3\alpha_1 + E\alpha_1 = \lambda_1^5\alpha_1 - 4\lambda_1^3\alpha_1 + \alpha_1 = (1 - 4 + 1)\alpha_1 = -2\alpha_1,

所以 $\alpha_1$ 是 $B$ 的特征向量，对应的特征值为 $-2$ 。
$B$ 是 $A$ 的多项式，因此 $B$ 的特征值可以通过 $A$ 的特征值计算。设 $f(\lambda) = \lambda^5 - 4\lambda^3 + 1$ ，则

f(1) = 1^5 - 4 \cdot 1^3 + 1 = -2, \quad f(2) = 2^5 - 4 \cdot 2^3 + 1 = 1, \quad f(-2) = (-2)^5 - 4 \cdot (-2)^3 + 1 = 1,

所以 $B$ 的特征值为 $-2, 1, 1$ 。
特征向量：对于特征值 $-2$ ，特征向量为 $k\alpha_1$ （ $k \neq 0$ ）。对于特征值 $1$ ，由于 $A$ 是实对称矩阵，其特征向量相互正交，且 $B$ 的特征向量与 $A$ 相同，因此特征值 $1$ 的特征向量是 $A$ 的属于特征值 $2$ 和 $-2$ 的特征向量，这些特征向量均与 $\alpha_1$ 正交，即满足 $x_1 - x_2 + x_3 = 0$ 。由于特征值 $1$ 是二重的，特征空间是二维的，所以任何满足 $x_1 - x_2 + x_3 = 0$ 的向量都是 $B$ 的属于特征值 $1$ 的特征向量。

(2) 由 (1) 知 $B$ 的特征值为 $-2, 1, 1$ ，且特征向量对应。令 $u_1 = \frac{\alpha_1}{\|\alpha_1\|} = \left( \frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \right)^T$ ，则 $B$ 可表示为

B = I - 3 u_1 u_1^T,

其中 $I$ 为单位矩阵。计算 $u_1 u_1^T$ ：

u_1 u_1^T = \begin{pmatrix} \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{pmatrix} = \begin{pmatrix} \frac{1}{3} & -\frac{1}{3} & \frac{1}{3} \\ -\frac{1}{3} & \frac{1}{3} & -\frac{1}{3} \\ \frac{1}{3} & -\frac{1}{3} & \frac{1}{3} \end{pmatrix},

则

B = I - 3 \cdot \begin{pmatrix} \frac{1}{3} & -\frac{1}{3} & \frac{1}{3} \\ -\frac{1}{3} & \frac{1}{3} & -\frac{1}{3} \\ \frac{1}{3} & -\frac{1}{3} & \frac{1}{3} \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} - \begin{pmatrix} 1 & -1 & 1 \\ -1 & 1 & -1 \\ 1 & -1 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix}.

因此，矩阵 $B$ 为

\begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & 1 \\ -1 & 1 & 0 \end{pmatrix}.

23

（本题满分 11 分）

设二维随机变量 $(X,Y)$ 的概率密度为

f(x,y) = \begin{cases} 2 - x - y, & 0 < x < 1,0 < y < 1, \\ 0, & \text{其他}. \end{cases}

(1) 求 $P\{X > 2Y\}$ ；

(2) 求 $Z = X + Y$ 的概率密度 $f_Z(z)$ ．

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

【答案】
(1) $P\{X > 2Y\} = \frac{7}{24}$
(2) $Z = X + Y$ 的概率密度函数为

f_Z(z) = \begin{cases} z(2 - z), & 0 < z < 1 \\ (2 - z)^2, & 1 < z < 2 \\ 0, & \text{} \end{cases}

【解析】
(1) 计算 $P\{X > 2Y\}$ ，即求概率 $P\{X > 2Y\} = \iint_{x > 2y} f(x,y) \, dx \, dy$ 。由于 $f(x,y)$ 在 $0 < x < 1, 0 < y < 1$ 时非零，且满足 $x > 2y$ ，因此积分区域为 $0 < y < 0.5$ 和 $2y < x < 1$ 。于是：

P\{X > 2Y\} = \int_{0}^{0.5} \int_{2y}^{1} (2 - x - y) \, dx \, dy

先计算内层积分：

\int_{2y}^{1} (2 - x - y) \, dx = \left[ 2x - \frac{1}{2}x^2 - yx \right]_{x=2y}^{x=1} = (1.5 - y) - (4y - 4y^2) = 1.5 - 5y + 4y^2

然后计算外层积分：

\int_{0}^{0.5} (1.5 - 5y + 4y^2) \, dy = \left[ 1.5y - \frac{5}{2}y^2 + \frac{4}{3}y^3 \right]_{0}^{0.5} = \frac{3}{4} - \frac{5}{8} + \frac{1}{6} = \frac{18}{24} - \frac{15}{24} + \frac{4}{24} = \frac{7}{24}

故 $P\{X > 2Y\} = \frac{7}{24}$ 。

(2) 求 $Z = X + Y$ 的概率密度 $f_Z(z)$ 。使用卷积公式， $f_Z(z) = \int_{-\infty}^{\infty} f(x, z-x) \, dx$ 。其中 $f(x, z-x) = 2 - x - (z-x) = 2 - z$ ，但需满足 $0 < x < 1$ 和 $0 < z-x < 1$ ，即 $\max(0, z-1) < x < \min(1, z)$ 。因此：

f_Z(z) = \int_{\max(0, z-1)}^{\min(1, z)} (2 - z) \, dx = (2 - z) \left[ \min(1, z) - \max(0, z-1) \right]

根据 $z$ 的取值范围讨论：

当 $0 < z < 1$ 时， $\min(1, z) = z$ ， $\max(0, z-1) = 0$ ，所以 $f_Z(z) = (2 - z) z = z(2 - z)$ 。
当 $1 < z < 2$ 时， $\min(1, z) = 1$ ， $\max(0, z-1) = z-1$ ，所以 $f_Z(z) = (2 - z) (1 - (z-1)) = (2 - z)^2$ 。
当 $z \leq 0$ 或 $z \geq 2$ 时， $f_Z(z) = 0$ 。
验证概率密度积分为 1：
$\int_{0}^{1} z(2-z) \, dz = \int_{0}^{1} (2z - z^2) \, dz = \left[ z^2 - \frac{1}{3}z^3 \right]_{0}^{1} = 1 - \frac{1}{3} = \frac{2}{3}$ $\int_{1}^{2} (2-z)^2 \, dz = \int_{1}^{2} (z-2)^2 \, dz = \left[ \frac{1}{3}(z-2)^3 \right]_{1}^{2} = 0 - \left( \frac{1}{3}(-1)^3 \right) = \frac{1}{3}$ 总和为 $\frac{2}{3} + \frac{1}{3} = 1$ ，正确。故 $f_Z(z)$ 如上所述。

24

（本题满分 11 分）

设总体 $X$ 的概率密度为

f(x;\theta) = \begin{cases} \frac{1}{2\theta}, & 0 < x < \theta , \\ \frac{1}{2(1-\theta)}, & \theta \le x < 1, \\ 0, & \text{其他}. \end{cases}

其中参数 $\theta$ （ $0 < \theta < 1$ ）未知， $X_1,X_2,\cdots X_n$ 是来自总体 $X$ 的简单随机样本， $\overline{X}$ 是样本均值．

(1) 求参数 $\theta$ 的矩估计量 $\widehat{\theta}$ ；

(2) 判断 $4\overline{X}^2$ 是否为 $\theta^2$ 的无偏估计量，并说明理由．

概率论与数理统计参数估计与假设检验矩估计和最大似然估计

【答案】 (1) 参数 $\theta$ 的矩估计量为 $\widehat{\theta} = \frac{4\overline{X} - 1}{2}$ 。 (2) $4\overline{X}^2$ 不是 $\theta^2$ 的无偏估计量。

【解析】 (1) 求矩估计量

总体均值为

E(X) = \int_{0}^{\theta} x \cdot \frac{1}{2\theta} \, dx + \int_{\theta}^{1} x \cdot \frac{1}{2(1-\theta)} \, dx.

计算得第一个积分为 $\frac{\theta}{4}$ ，第二个积分为 $\frac{1+\theta}{4}$ ，于是

E(X) = \frac{\theta}{4} + \frac{1+\theta}{4} = \frac{1+2\theta}{4}.

根据矩估计法，令样本均值 $\overline{X} = E(X)$ ，即

\overline{X} = \frac{1+2\theta}{4},

解得

\theta = \frac{4\overline{X} - 1}{2}.

因此矩估计量为

\widehat{\theta} = \frac{4\overline{X} - 1}{2}.

(2) 判断无偏性

需要判断 $4\overline{X}^2$ 是否为 $\theta^2$ 的无偏估计量，即计算 $E(4\overline{X}^2)$ 。

首先，

E(\overline{X}) = E(X) = \frac{1+2\theta}{4}, \quad \operatorname{Var}(\overline{X}) = \frac{\operatorname{Var}(X)}{n}.

计算总体方差 $\operatorname{Var}(X) = E(X^2) - [E(X)]^2$ ，其中

E(X^2) = \int_{0}^{\theta} x^2 \cdot \frac{1}{2\theta} \, dx + \int_{\theta}^{1} x^2 \cdot \frac{1}{2(1-\theta)} \, dx.

计算得第一个积分为 $\frac{\theta^2}{6}$ ，第二个积分为 $\frac{1+\theta+\theta^2}{6}$ ，于是

E(X^2) = \frac{\theta^2}{6} + \frac{1+\theta+\theta^2}{6} = \frac{1+\theta+2\theta^2}{6}.

因此，

\operatorname{Var}(X) = \frac{1+\theta+2\theta^2}{6} - \left( \frac{1+2\theta}{4} \right)^2 = \frac{5 - 4\theta + 4\theta^2}{48}.

于是

\operatorname{Var}(\overline{X}) = \frac{5 - 4\theta + 4\theta^2}{48n},

E(\overline{X}^2) = \operatorname{Var}(\overline{X}) + [E(\overline{X})]^2 = \frac{5 - 4\theta + 4\theta^2}{48n} + \left( \frac{1+2\theta}{4} \right)^2.

所以

E(4\overline{X}^2) = 4E(\overline{X}^2) = \frac{5 - 4\theta + 4\theta^2}{12n} + \frac{1 + 4\theta + 4\theta^2}{4}.

整理得

E(4\overline{X}^2) = \frac{3n + 5 + (12n - 4)\theta + (12n + 4)\theta^2}{12n}.

可见 $E(4\overline{X}^2)$ 是 $\theta$ 的二次函数，且包含常数项与一次项，而 $\theta^2$ 是纯二次项。因此对于任意有限 $n$ ，

E(4\overline{X}^2) \neq \theta^2,

故 $4\overline{X}^2$ 不是 $\theta^2$ 的无偏估计量。